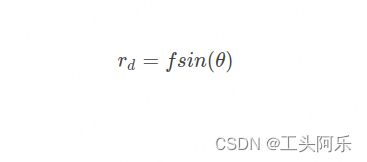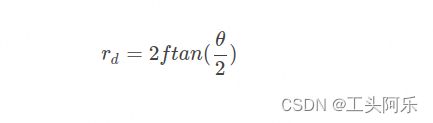鱼眼相机成像模型以及基于OpenCV标定鱼眼镜头（C++）

opencv系列

---

---

一、鱼眼镜头模型

鱼眼镜头一般是由十几个不同的透镜组合而成的，在成像的过程中，入射光线经过不同程度的折射，投影到尺寸有限的成像平面上，使得鱼眼镜头与普通镜头相比起来拥有了更大的视野范围。下图表示出了鱼眼相机的一般组成结构。最前面的两个镜头发生折射，使入射角减小，其余的镜头相当于一个成像镜头，这种多元件的构造结构使对鱼眼相机的折射关系的分析变得相当复杂。

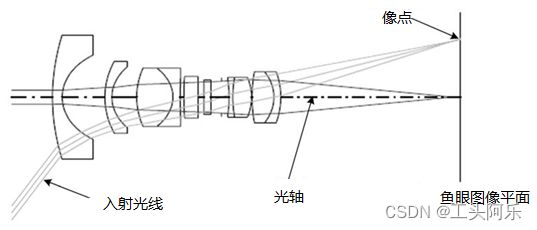
研究表明鱼眼相机成像时遵循的模型可以近似为单位球面投影模型。可以将鱼眼相机的成像过程分解成两步：第一步，三维空间点线性地投影到一个球面上，它是一个虚拟的单位球面，它的球心与相机坐标系的原点重合；第二步，单位球面上的点投影到图像平面上，这个过程是非线性的。下图表示出了鱼眼相机的成像过程。

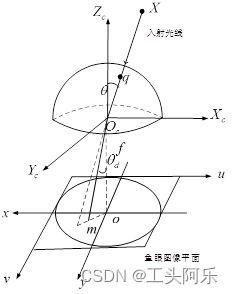
我们知道，普通相机成像遵循的是针孔相机模型，在成像过程中实际场景中的直线仍被投影为图像平面上的直线。但是鱼眼相机如果按照针孔相机模型成像的话，投影图像会变得非常大，当相机视场角达到180°时，图像甚至会变为无穷大。所以，鱼眼相机的投影模型为了将尽可能大的场景投影到有限的图像平面内，允许了相机畸变的存在。并且由于鱼眼相机的径向畸变非常严重，所以鱼眼相机主要的是考虑径向畸变，而忽略其余类型的畸变。

二、投影函数

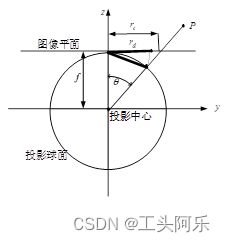
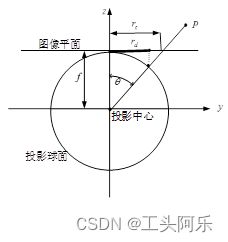
为了将尽可能大的场景投影到有限的图像平面内，鱼眼相机会按照一定的投影函数来设计。根据投影函数的不同，鱼眼相机的设计模型大致能被分为四种：等距投影模型、等立体角投影模型、正交投影模型和体视投影模型。下面的四种鱼眼相机的投影模型反映出了空间中的一点P是如何投影到球面上，然后到图像平面上成像的。

等距投影模型

上述式子中，rd表示鱼眼图像中的点到畸变中心的距离，是鱼眼相机的焦距，是入射光线与鱼眼相机光轴之间的夹角，即入射角。

等立体角投影模型

正交投影模型

体视投影模型

三、OpenCV中的鱼眼相机模型

OpenCV中使用的模型是由Kannala提出的一种鱼眼相机的一般近似模型。在等距投影模型的基础上提出来的。下面来详细分析其鱼眼相机模型的提出过程。我们可以将鱼眼相机模型的形式统一以等距投影模型的形式来表示，即

对实际的鱼眼镜头来说，它们不可能精确地按照投影模型来设计，所以为了方便鱼眼相机的标定，Kannala提出了一种鱼眼相机的一般多项式近似模型。通过前面的四个模型，可以发现 θd是θ的奇函数，而且将这些式子按泰勒级数展开，发现 θd可以用θ 的奇次多项式表示，即

为了实际计算的方便，需要确定式中 θd取到的次幂数。Kannala提出取式的前五项即取到的九次方，就给出了足够的自由度来很好地近似各种投影模型。 θd的一次项系数可以为1，于是OpenCV中使用的鱼眼相机模型为：

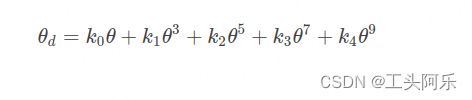
上式表示的模型是根据四种鱼眼相机投影模型得出的一种通用鱼眼相机多项式模型。这种模型根据θ能够得到 θd ，即通过无畸变图像中的点能够计算出鱼眼图像中的畸变点。这种模型在OpenCV的鱼眼相机标定方法中是适用的，因为OpenCV借助标定板对鱼眼相机进行标定。从空间点到鱼眼图像上的点的变换过程可用式子表示为：

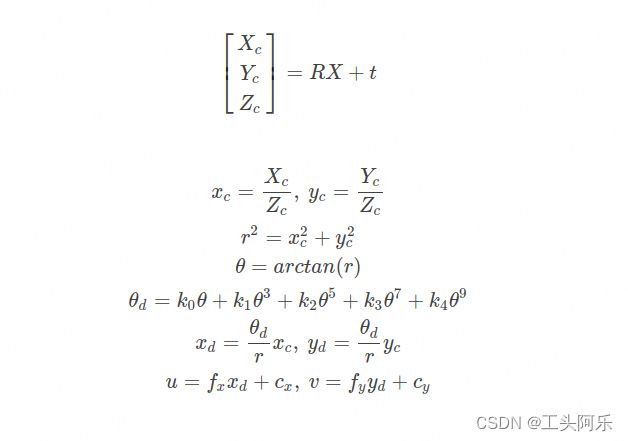
上面式子中， X表示空间点，Xc表示相机坐标系下对应的空间点， R和t分别是两个坐标系之间的旋转矩阵和平移向量， (u,v)T 表示投影到鱼眼图像上的对应点。OpenCV中对鱼眼相机的标定步骤能够分成四步：

（1）初始化内参数；
（2）初始化外参数；
（3）使用LM算法最小化定位的图像点和投影的图像点之间的投影误差；
（4）确定结果。

四、标定（C++）实现

使用的函数

由于鱼眼镜头和针孔镜头的模型不一样，对于鱼眼镜头的模型在之前的博客中已经做了详细介绍，这里直接使用OpenCV中的cv::fisheye::calibrate()函数进行标定。函数原型如下，需要输入目标点集，图像点集、图像尺寸。函数输出相机内参，畸变系数，旋转矩阵和平移向量，以及反投影误差。

 CV_EXPORTS double calibrate(InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, const Size& image_size,
        InputOutputArray K, InputOutputArray D, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags = 0,
            TermCriteria criteria = TermCriteria(TermCriteria::COUNT + TermCriteria::EPS, 100, DBL_EPSILON));

采集标定图像

采集若干拍摄有标定棋盘格的图像，并使棋盘格出现在画面的各个位置，特别是边缘位置。如下图所示：

标定代码

#include "stdio.h"
#include 
#include 
#include 

#include "opencv2/opencv.hpp"
#include 
#include "opencv2/calib3d/calib3d.hpp"
#include 

using namespace std;
using namespace cv;

void getFiles(string path, vector<string>& files)
{
    //文件句柄
    intptr_t hFile = 0;
    //文件信息
    struct _finddata_t fileinfo;
    string p;
    if ((hFile = _findfirst(p.assign(path).append("\\*").c_str(), &fileinfo)) != -1)
    {
        do
        {
            //如果是目录,迭代之
            //如果不是,加入列表
            if ((fileinfo.attrib &  _A_SUBDIR))
            {
                if (strcmp(fileinfo.name, ".") != 0 && strcmp(fileinfo.name, "..") != 0)
                    getFiles(p.assign(path).append("\\").append(fileinfo.name), files);
            }
            else
            {
                files.push_back(p.assign(path).append("\\").append(fileinfo.name));
            }
        } while (_findnext(hFile, &fileinfo) == 0);
        _findclose(hFile);
    }
}

int main(int argc, char** argv)
{   
    string filePath = ".\\720PPcalib\\front";
    vector<string> files;

    获取该路径下的所有文件
    getFiles(filePath, files);

    const int board_w = 6;
    const int board_h = 4;
    const int NPoints = board_w * board_h;//棋盘格内角点总数
    const int boardSize = 30; //mm
    Mat image,grayimage;
    Size ChessBoardSize = cv::Size(board_w, board_h);
    vector<Point2f> tempcorners;

    int flag = 0;
    flag |= cv::fisheye::CALIB_RECOMPUTE_EXTRINSIC;
    //flag |= cv::fisheye::CALIB_CHECK_COND;
    flag |= cv::fisheye::CALIB_FIX_SKEW;
    //flag |= cv::fisheye::CALIB_USE_INTRINSIC_GUESS;

    vector<Point3f> object;
    for (int j = 0; j < NPoints; j++)
    {
        object.push_back(Point3f((j % board_w) * boardSize, (j / board_w) * boardSize, 0)); 
    }

    cv::Matx33d intrinsics;//z:相机内参
    cv::Vec4d distortion_coeff;//z:相机畸变系数

    vector<vector<Point3f> > objectv;
    vector<vector<Point2f> > imagev;

    Size corrected_size(1280, 720);
    Mat mapx, mapy;
    Mat corrected;

    ofstream intrinsicfile("intrinsics_front1103.txt");
    ofstream disfile("dis_coeff_front1103.txt");
    int num = 0;
    bool bCalib = false;
    while (num < files.size())
    {
        image = imread(files[num]);

        if (image.empty())
            break;
        imshow("corner_image", image);
        waitKey(10);
        cvtColor(image, grayimage, CV_BGR2GRAY);
        IplImage tempgray = grayimage;
        bool findchessboard = cvCheckChessboard(&tempgray, ChessBoardSize);

        if (findchessboard)
        {
            bool find_corners_result = findChessboardCorners(grayimage, ChessBoardSize, tempcorners, 3);
            if (find_corners_result)
            {
                cornerSubPix(grayimage, tempcorners, cvSize(5, 5), cvSize(-1, -1), cvTermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));
                drawChessboardCorners(image, ChessBoardSize, tempcorners, find_corners_result);
                imshow("corner_image", image);
                cvWaitKey(100);

                objectv.push_back(object);
                imagev.push_back(tempcorners);
                cout << "capture " << num << " pictures" << endl;
            }
        }
        tempcorners.clear();
        num++;
    }

    cv::fisheye::calibrate(objectv, imagev, cv::Size(image.cols,image.rows), intrinsics, distortion_coeff, cv::noArray(), cv::noArray(), flag, cv::TermCriteria(3, 20, 1e-6));  
    fisheye::initUndistortRectifyMap(intrinsics, distortion_coeff, cv::Matx33d::eye(), intrinsics, corrected_size, CV_16SC2, mapx, mapy);

    for(int i=0; i<3; ++i)
    {
        for(int j=0; j<3; ++j)
        {
            intrinsicfile<<intrinsics(i,j)<<"\t";
        }
        intrinsicfile<<endl;
    }
    for(int i=0; i<4; ++i)
    {
        disfile<<distortion_coeff(i)<<"\t";
    }
    intrinsicfile.close();
    disfile.close();

    num = 0;
    while (num < files.size())
    {
        image = imread(files[num++]);

        if (image.empty())
            break;
        remap(image, corrected, mapx, mapy, INTER_LINEAR, BORDER_TRANSPARENT);

        imshow("corner_image", image);
        imshow("corrected", corrected);
        cvWaitKey(200); 
    }

    cv::destroyWindow("corner_image");
    cv::destroyWindow("corrected");

    image.release();
    grayimage.release();
    corrected.release();
    mapx.release();
    mapy.release();

    return 0;
}

标定结果

使用标定的结果进行畸变校正后的结果如下所示，可以看到，原本弯曲的曲线已经变直。