【CMU15-445数据库】bustub Project #2:B+ Tree(上)
(最近两个月学校项目有亿点忙,鸽得有点久,先来把 Project 2 补上)
本节实验文档地址:Project #2 - B+Tree
Project 2 要实现的是数据结构课上都会讲的一个经典结构 B+ 树,但是相信大多数的同学(包括博主)当时都没有自己动手实现过它,本节就是一个很好的锻炼机会。
本节内容会大量使用到 Project 1 实现的 BufferPoolManager(当然也包含了其内部用到的 ExtendibleHashTable 和 LRUKReplacer),所以需要完成前置内容(博主也比较建议这样做,否则直接上手本节可能不好理解对 Page 的 Fetch 和 Unpin 操作)。
由于代码量较多,打算拆成上下两篇写完,本篇介绍用到的数据结构和 B+ 树的查找和插入实现,下一篇讲迭代器,删除和并发控制。
关于 B+ 树的文字介绍就不赘述了,查阅资料过程中发现维基百科的 B+ 树词条的算法描述不够具体,推荐一个有比较具体的例子的博客:
B树和B+树的插入、删除图文详解
(同时不建议参考那些插入和删除分 N 多种具体情况讨论的介绍)
数据结构
B+ 树中有内部节点和叶节点两种结构,它们存储的数据格式和内容不同。bustub 为我们设计好了下面这三个类:
-
节点基类
BPlusTreePage

内部节点和叶节点的基类,包含了节点类型、当前容量、最大/最小容量、ID、父节点 ID 信息,从类结构上可以看做是两种节点的头信息。按照函数字面意思将其实现即可。可以规定parent_page_id_为INVALID_PAGE_ID表示根节点。 -
内部节点
BPlusTreeInternalPage
![]()

内部节点,首先看用到的三个泛型 KeyType, ValueType, KeyComparator。KeyType 不一定直接可用大于小于号比较,所以引入了 KeyComparator,从 cpp 文件中的实例化可以看出用的是 GenericKey 和 GenericComparator,查看二者源码可以得到以下信息:
GenericKey可以调用ToString()函数得到其int64表示,然后用%ld格式符打印。这对我们后面调试时非常重要。GenericComparator的比较规则是:左边小于右边时,返回 -1;左边大于右边时,返回 1;相等返回 0。
ValueType 代表的是指向子页面的指针,从实例化可以看出实际只用了 page_id_t,也就是 int。
数据存储上,其理论结构应为 <指针,键,指针,键…,键,指针>,为方便存储,实际上在头部多补了一个无效键,从而可以用一个 pair 的数组存储:
#define MappingType std::pair<KeyType, ValueType>
...
class BPlusTreeInternalPage : public BPlusTreePage {
...
private:
// Flexible array member for page data.
MappingType array_[1];
}
array_[1] 等价于一个指针,按照一般习惯应该在构造函数中为其 new 出一片大小为 max_size_ 的空间,但实际上不需要这样做,因为:
Each B+Tree leaf/internal page corresponds to the content (i.e., the data_ part) of a memory page fetched by buffer pool. So every time you try to read or write a leaf/internal page, you need to first fetch the page from buffer pool using its unique page_id, then reinterpret cast to either a leaf or an internal page, and unpin the page after any writing or reading operations.
简单翻译一下就是 内部节点和叶节点对象都不是直接创建出来,而是由一个 Buffer Pool 管理的 Page 的 data 部分类型转化而来(所以要用到很少用很暴力的 reinterpret_cast)。所以,节点对象使用的是预先分配好的固定空间,array_ 可以控制从该位置开始到 Page 的 data 结束为止的这一段空间。因此,节点对象的生命周期也不是由 new 和 delete,而是由我们上节实现的 BufferPoolManager 管理:取一个页面,用 FetchPage;使用结束归还一个页面,用 UnpinPage。同时也就能理解 BPlusTreePage 中 page_id_ 成员的另一个含义:它不仅是 B+ 树中节点的编号,同时也是这个节点使用的 Page 在 BufferPool 中的编号。
- 叶节点
BPlusTreeLeafPage

数据存储上,叶节点也是一个 键+值 的数组,但不像内部节点那样第一个键无效。值的类型实际用的也只有一种:RID。这个和我们本节的内容关系不大,大致知道它是代表数据实际存放的位置即可。
BPlusTree 类代表整个 B+ 树:
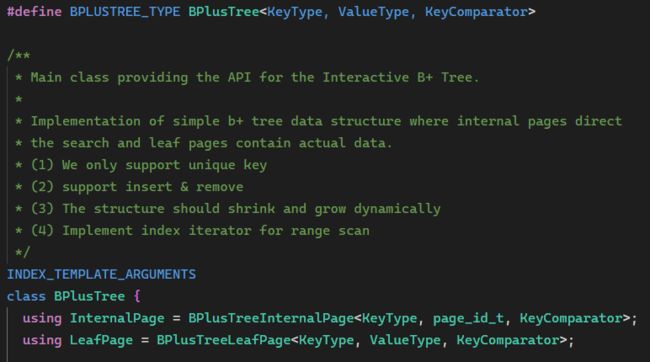
其主要成员有:buffer_pool_manager_,由外部传入;root_page_id,表示根节点 ID;comparator_,KeyComparator 类型的对象,用于键的大小比较;leaf_max_size_ 和 internal_max_size_,表示叶节点和内部节点的最大容量。我们需要实现 B+ 树的四个功能:查找,插入,删除和迭代器。
Checkpoint 1:查找,插入和删除
实验非常贴心地将所有内容分为了两个 checkpoint,其中 checkpoint 1 要实现查找,插入和删除功能,checkpoint 2 要实现迭代器和并发控制,Autograder 上也对应有两个提交位置。下面放出的代码都只通过 checkpoint 1,没有考虑加锁,这样能更专注于讲解其本身的逻辑。本篇先讲查找和插入。
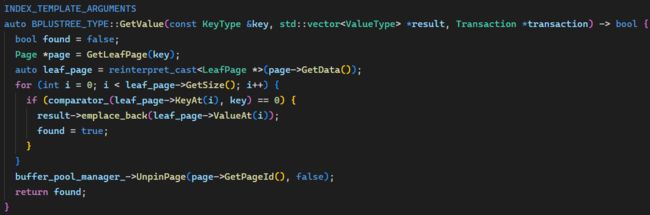
查找(GetValue)
给定一个键 x x x,查找其是否在 B+ 树中存在。实现逻辑是先找到键可能在的叶节点,然后扫描一遍叶节点的内容确定是否存在,其中重点是前者。编写一个函数 GetLeafPage,根据 B+ 树的规则,应该从根节点开始,每次在内部节点中找到 k i < x < k i + 1 k_i < x < k_i+1 ki<x<ki+1 的位置,然后沿着 v i v_i vi 指针继续向下,直到达到叶节点。函数实现如下:
Tips:循环时找内部节点中第一个比 x x x 大的键,取其左侧的值即可( k [ 0 ] k[0] k[0]无效),而这样不能探测到 x x x 比所有 k k k 都大的情况,所以要将
next_page_id初始化为最右侧的键
在此基础上,GetValue 的实现就很简单了:
插入(Insert)
热身完毕,下面进入本节第一个难点,插入的实现。B+ 树的插入流程为:
- 如果是空树,创建一个叶节点作为根。注意涉及
root_page_id_更新时都要调用一次UpdateRootPageId,如果是第一次创建传 1 作为参数,更新不用,以下不再复述。 - 从根节点向下查找到键值应该所在的叶节点。文档说明了不支持重复键,所以先扫描一遍叶节点,如果发现键存在则直接返回 false。
- 如果叶节点 插入后 达到了 max_size,则要进行分裂(split),创建一个新的叶节点,将原节点的一半内容拷贝到新节点,分裂点的键插入父节点,该键对应的值指向新的叶节点。(如果父节点不存在,说明是第一个叶节点兼根节点,需要创建一个新的根,这种情况和 4 的建根可以合并处理)
- 如果父节点(内部节点)插入前 达到了 max_size,也要递归进行分裂并向上插入,此时还要调整原节点的一半子节点的
parent_id_指针指向新的内部节点。如果根节点满了,则要创建一个新的根节点,使得 B+ 树长高一层。
Tips:特别注意这里叶节点和内部节点的判断条件是不同的,摘一段文档原文:
You should correctly perform splits if insertion triggers the splitting condition (number of key/value pairs AFTER insertion equals to max_size for leaf nodes, number of children BEFORE insertion equals to max_size for internal nodes).
第 1、2 步代码:
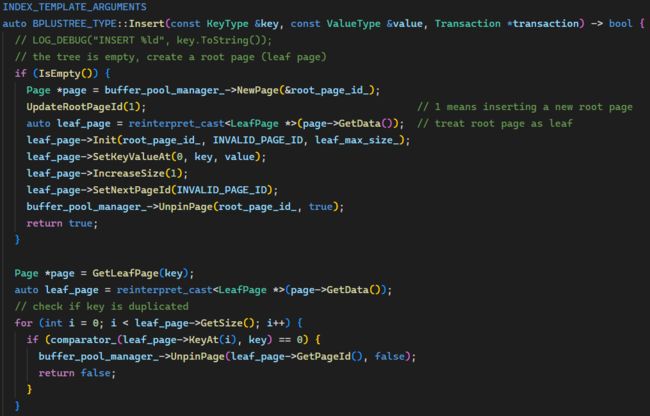
第 3 步,未溢出情况,插入的具体逻辑可以放到 LeafPage 类中做,所以添加一个 Insert 函数,找到插入位置,将所有后面的键值对后移一位,再设置。由于 array_ 是有序的,如果还想提高效率,可以把找插入位置用二分搜索实现。
Tips:
comparator_也要作为参数传入Insert,否则LeafPage中无法进行键的比较,也就无法查找

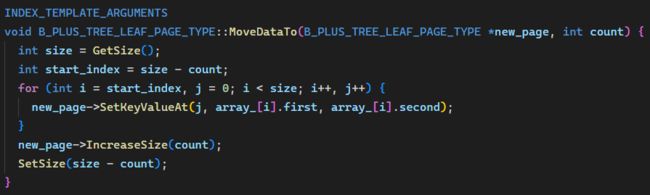
叶节点溢出情况,注意处理好 next_page_id_。移动一半数据的逻辑也可以放到 LeafPage 类中,添加一个 MoveDataTo 函数:
Tips:
MoveDataTo不用真的对原叶节点后一半数据进行“抹除”,修改 size 即可,以后的新数据自然会覆盖掉这些数据。
真正的难点来了:如何处理向父节点插入、同时处理父节点可能继续分裂的递归逻辑。需要想清楚的是:在两次递归之间,需要传递的数据是什么?我的设计是,传递两个子节点对象和分裂点的键。前者是为了获取到其父节点,也可以对其本身的父节点指针进行更新,后者是要插入父节点的键。进一步思考,在第一轮,传递的子节点对象是叶节点,而后面每轮是内部节点,看起来不统一,但实际上我们需要这两个子节点只涉及到 page_id 的父子指针的更改,所以,传递的形式应设计为基类指针 BPlusTreePage *,就可以兼顾这两种情况。
这里我用一个 while(true) 循环实现,写成函数递归调用当然也可以。三个传递数据分别命名为 old_tree_page,new_tree_page 和 split_key。
第一轮初始化和到达根节点的处理。正因为用的是 BPlusTreePage *,所以可以兼顾 3 和 4,即上一层是叶节点和内部节点两种情况的建根。
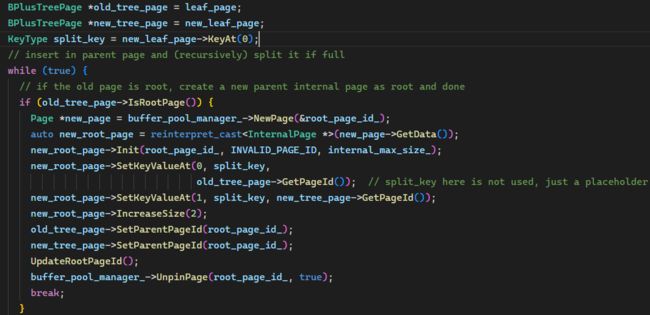
未到达根节点,则在父节点进行插入。这里类似地我在 InternalPage 中也添加了一个 Insert 函数,但要注意逻辑上有一丁点不同,就是查找插入位置要从 1 开始。

如果父节点也溢出,创建新的内部节点并移动一半数据。这里涉及到子节点的指针修改,所以直接把逻辑写在这里了。最后将三个传递数据更新,准备做下一轮处理。

细心的读者可能注意到上面达到跳出循环条件后没有 return true 而是写了 break,这是因为在最后一轮循环结束后还要统一做一件事情:释放最后两个页面。

如果你做完后本地测试和 AutoGrader 其它测试都能通过,只有 ScaleTest 报错 SIGSEGV,InternalPage 或 LeafPage 的函数(比如 GetSize())访问了空地址,则很可能是 Insert 函数中没有把所有 Fetch 的 Page 最后 Unpin 掉,导致其一直占着 BufferPoolManager 的空间,最终空间耗尽无法取到新页面,FetchPage 返回 nullptr。检查也很简单,改一下 BufferPoolManagerInstance 的代码,例如每次 Fetch 和 Unpin 时打印一个信息,看一下是不是所有的页面都被释放了(0 号页面不被释放是正常的)。
Debug 方法
这里我要吹爆 bustub 的开发组,他们提供了一个非常好用的工具 b_plus_tree_printer,可视化展现树的结构,帮助检查你的实现效果是否正确。