符号集合近似法SAX
0. 内容
- 时间序列局部特征构造的方法:SAX算法(符号集合近似法)
- 符号集合近似法下的距离定义
- 符号集合近似法除了可以降低时间序列的维度之外,还有数据压缩作用
一些时间序列分类问题可能涉及时间序列属性的差异,这些属性被限制在特定的有区别时间区间内,即所谓的局部特征。
1. SAX算法1
笼统地理解,SAX((Symbolic Aggregate approXimation,符号集合近似)算法是将时间序列转换为字符串。和傅里叶变换、小波变换类似的地方是:都是一种变换。但是和由时域变换到频域不同,SAX是将其变换成字符串。其优点是可以借助丰富的字符串的数据结构和算法来分析时间序列。
SAX算法的实现的效果:
- 降低原始序列数据的维度;
- 保留了数据的局部特征信息;
- 对 数据噪声有一定承受能力,分段既消除噪声又实现了数据平滑;
- 使得字符化后的序列上定义的距离和原始序列距离有强相关性,进一步说是保持序列变换前后的下界距离一致性;
符号约定:
- C = c 1 , c 2 , . . . , c n C=c_1,c_2,...,c_n C=c1,c2,...,cn是一个时间序列
- C ˉ = c ˉ 1 , c ˉ 2 , . . . , c ˉ w \bar C=\bar c_1, \bar c_2,...,\bar c_w Cˉ=cˉ1,cˉ2,...,cˉw是一个分段聚集近似序列(Piecewise Aggreate Approximation, PAA)
- C ^ = c ^ 1 , c ^ 2 , . . . , c ^ w \hat C=\hat c_1,\hat c_2,...,\hat c_w C^=c^1,c^2,...,c^w符号表示得到的序列
- w w w:PAA表示原始时间序列 C C C的片段数目
- a a a:字母表集合大小 ,例如,字母表集合 ={ a , b , c a,b,c a,b,c},则 a = 3 a=3 a=3;
粗略描述SAX算法流程:
- 将原始时间序列Z-score标准化;
- 将标准化后的时间序列 C C C转换成PAA序列 C ˉ \bar C Cˉ(分段聚集近似序列);
- 然后将PAA序列 C ˉ \bar C Cˉ转换成字符序列 C ^ \hat C C^;
下面是细致的阐述:
1.1 PAA近似序列 C ˉ \bar C Cˉ
将n维 C = c 1 , c 2 , . . . , c n C=c_1,c_2,...,c_n C=c1,c2,...,cn时间序列向量,转换为w维的向量 C ˉ = c ˉ 1 , c ˉ 2 , . . . , c ˉ w \bar C=\bar c_1, \bar c_2,...,\bar c_w Cˉ=cˉ1,cˉ2,...,cˉw,其中,第 i i i个 c ^ i \hat c_i c^i是按照下式计算:
c ˉ i = w n ∑ j = n w ( i − 1 ) + 1 n w i c j \bar c_i = \frac{w}{n}\sum_{j=\frac{n}{w}(i-1)+1}^{\frac{n}{w}i}c_j cˉi=nwj=wn(i−1)+1∑wnicj
公式表达的意思是,为了将n维原始的时间序列向量降到w维,将原始时间序列向量划分为w个片段,第 i i i片段内的均值对应于 c ˉ i \bar c_i cˉi的值。其中,将 n w \frac{n}{w} wn称为压缩率,必须保证为整数。如果n是素数,我们可以通过长度为合数的滑窗来提取时间序列的子序列进行PAA近似序列的求解。

1.2 字符序列 C ^ \hat C C^
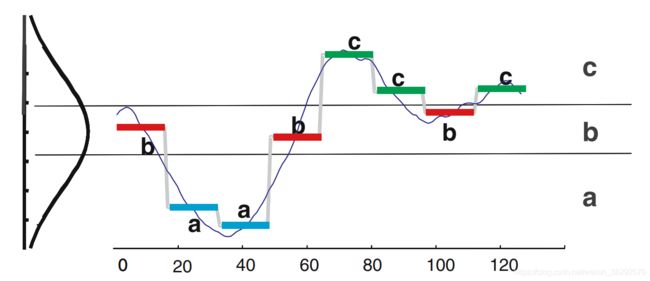
通过求取使得高斯分布被划分成等概率区间的断点序列 B B B,然后通过断点序列B和PAA近似序列值完成符号化。
定义1: 断点序列(Breakpoints):断点序列是有序的数字序列 B = β 1 , β 2 , . . . , β a − 1 B=\beta_1, \beta_2, ..., \beta_{a-1} B=β1,β2,...,βa−1, 其中 β i \beta_i βi和 β i + 1 \beta_{i+1} βi+1之间对应的高斯分布的概率值间隔等于 1 a \frac{1}{a} a1。特别地,规定 β 0 , β a \beta_0,\beta_a β0,βa分别表示 − ∞ , + ∞ -\infty,+\infty −∞,+∞。
我的理解:
- 断点序列 a − 1 a-1 a−1个值对应将标准高斯分布的随机变量值;
- 任意相邻两个断点之间对应的标准高斯分布概率值是相等的;
- 图2示例了这一过程的结果
定义2: 字符化。存在一个有序字符集合alpha,例如, a l p h a 1 = a , a l p h a 2 = b alpha_1 = a, alpha_2 = b alpha1=a,alpha2=b, 通过下式完成PAA近似序列 C ˉ \bar C Cˉ到字符序列 C ^ \hat C C^的映射:
c ^ i = a l p h a j \hat c_i = alpha_j c^i=alphaj, 当且仅当, β j − 1 ≤ c ˉ i < β j \beta_{j-1} \leq \bar c_i < \beta_j βj−1≤cˉi<βj
至此,完成了时间序列的字符表示。

2. 符号集合近似法下的序列距离定义
第1小节引入了符号集合近似法,完成了对时间序列的符号表示。下面要定义符号化后的两个序列之间的距离。
2.1 字符的最近距离(low bound distance)
SAX定义的距离是字符最近距离(low bound distance),见图4所示。

对由PAA序列到字符的映射换个函数形式的定义:
定义2-1: c ^ i = t o _ w o r d ( c ˉ i ) \hat c_i = to\_word(\bar c_i) c^i=to_word(cˉi) , 当且仅当 c ˉ i ∈ [ β j − 1 , β j ) \bar c_i\in[\beta_{j-1},\beta_j) cˉi∈[βj−1,βj), t o _ w o r d ( c ˉ i ) = a l p h a j to\_word(\bar c_i)=alpha_j to_word(cˉi)=alphaj;
定义2-2: t o _ w o r d ( ) to\_word() to_word()的反函数 t o _ w o r d − 1 ( a l p h a j ) = { β l o w a l p h a j , β h i g h a l p h a j } = { β j − 1 , β j } to\_word^{-1}(alpha_j)=\{\beta_{low}^{alpha_j},\beta_{high}^{alpha_j}\}=\{\beta_{j-1},\beta_j\} to_word−1(alphaj)={βlowalphaj,βhighalphaj}={βj−1,βj}, 当且仅当, c ˉ i ∈ [ β j − 1 , β j ) \bar c_i\in[\beta_{j-1},\beta_j) cˉi∈[βj−1,βj);
利用定义2-1, 2-2 来定义字符最近距离 M I N D I S T ( Q ^ , P ^ ) MINDIST(\hat Q, \hat P) MINDIST(Q^,P^).
定义3 :字符最近距离 M I N D I S T ( Q ^ , P ^ ) = m i n ( β h i g h Q ^ , β h i g h P ^ ) − m a x ( β l o w Q ^ , β l o w P ^ ) MINDIST(\hat Q, \hat P)=min(\beta_{high}^{\hat Q}, \beta_{high}^{\hat P}) - max(\beta_{low}^{\hat Q}, \beta_{low}^{\hat P}) MINDIST(Q^,P^)=min(βhighQ^,βhighP^)−max(βlowQ^,βlowP^)
由图4可以直觉地发现, M I N D I S T ( Q ^ , P ^ ) MINDIST(\hat Q, \hat P) MINDIST(Q^,P^)是 Q ^ , P ^ \hat Q, \hat P Q^,P^的欧式距离下界。
3. 数据压缩
对于将时间序列降维,SAX算法是很明显的。除此之外,SAX还可以进行数据压缩。
3.1 直观的理解
对于一个很长的时间序列 T T T, 使用长度为 n n n的滑动窗口去提取子序列。使用SAX方法提取时,如果第一次提取到序列 a a b b c c aabbcc aabbcc,那么就不再存储后续提取的序列 a a b b c c aabbcc aabbcc,而是将其映射到第一次出现该序列的索引位置处。这样就实现了数据压缩。
3.2 SAX必须慎重考虑的特殊情况
时间序列的标准差特别小的时候,即几乎是常数的时间序列,例如,一个长度为32的序列,31个序列值是0, 只有一个序列值为0.0001。序列均值为3.125e-06,标准差为1.739926363384382e-05。
对其进行Z-score标准化后,会将噪声0.0001放大为5.567.如图5所示。
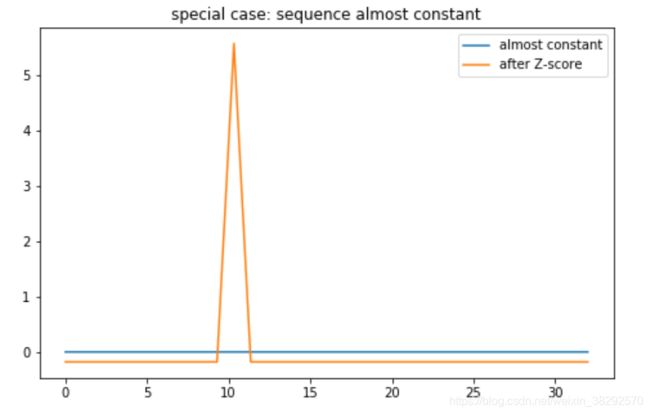
这种情况常常发生在对很长的时间序列进行滑窗提取子序列过程中。处理方式是:
当该时间序列的标准差低于 ϵ \epsilon ϵ时,将字母表的中间字母赋值给该时间序列。例如, α = 5 \alpha = 5 α=5, 即字母表为{a,b,c,d,e},映射成字符的长度 w = 6 w=6 w=6。令 ϵ = 2 e − 5 \epsilon = 2e-5 ϵ=2e−5,则图1中的时间序列赋值为 c c c c c c cccccc cccccc。