Catmull 细分曲面 (Catmull-Clark subdivision) 详解 附Python 完整代码
一、概述
图形学课程最后需要提交一个大作业,比较Catmull-Clark细分曲面与Loop细分曲面算法。先把Catmull-Clark细分曲面弄懂了,这里做个记录。昨天一直在网上找Catmull-Clark细分曲面相关的解释教程,但是并没有找到比较详细的计算过程说明,只有一些简单的示意图,并不能帮助我很好的理解,说实话,并没有看懂。知道后来,发现了Catmull–Clark subdivision surface这个网页,里面有各种语言版本的Catmull-Clark细分曲面的实现代码,其中Python版本是直接放出了完整的,我把代码拷贝运行了之后,运行的很好,想着看那么多教程也看不懂,看论文的话更慢,还不如直接看代码来的直接,我就把Python代码仔细从头到尾看了一遍,终于是弄懂了Catmull-Clark细分曲面的具体过程。在这之后,再返回来看三维网格细分算法(Catmull-Clark subdivision & Loop subdivision)附源码这篇文章,就大概知道这之间的关系是怎么一回事了。
注:未看详细算法,只记录如何做,不讨论为什么这么做。本文只是基于看了实现代码写出的,如果有错的地方请指正。
二、Catmull-Clark细分曲面过程
Catmull-Clark主要是针对四边形网格细分的算法
1. 计算面点(face_points)
计算面点比较简单,在后面计算边点(edge_points)时需要用到这一步的结果。

如上图所示,对于由四个顶点 V 0 , V 1 , V 2 , V 3 V_0,V_1,V_2,V_3 V0,V1,V2,V3 组成的面,记为 f f f,那么面 f f f的面点 f p fp fp 的计算为:
f p = 1 4 ( V 0 + V 1 + V 2 + V 3 ) fp=\frac{1}{4}(V_0+V_1+V_2+V_3) fp=41(V0+V1+V2+V3)
2. 计算边点(edge_points)

计算边点(edge_point)需要三个步骤,如上图所示
(1)首先计算边的中心点,如子图1所示,顶点 V 3 , V 2 V_3,V_2 V3,V2 形成的边 E ( V 3 , V 2 ) E_{(V_3,V_2)} E(V3,V2) 的中心点记为 e c ec ec,那么:
e c = 1 2 ( V 3 + V 2 ) ec=\frac{1}{2}(V_3+V_2) ec=21(V3+V2)
(2)计算边 E ( V 3 , V 2 ) E_{(V_3,V_2)} E(V3,V2) 相邻的两个面 f 1 , f 2 f_1,f_2 f1,f2 的面点 f p 1 , f p 2 fp_1,fp_2 fp1,fp2 的中心点 f p c fpc fpc,那么:
f p c = 1 2 ( f p 1 + f p 2 ) = 1 2 ( 1 4 ( V 0 + V 1 + V 2 + V 3 ) + 1 4 ( V 2 + V 3 + V 4 + V 5 ) ) = 1 8 ( V 0 + V 1 + V 4 + V 5 ) + 1 4 ( V 2 + V 3 ) \begin{aligned} fpc&=\frac{1}{2}(fp_1+fp_2)\\ &=\frac{1}{2}(\frac{1}{4}(V_0+V_1+V_2+V_3)+\frac{1}{4}(V_2+V_3+V_4+V_5)) \\&=\frac{1}{8}(V_0+V_1+V_4+V_5)+\frac{1}{4}(V_2+V_3) \end{aligned} fpc=21(fp1+fp2)=21(41(V0+V1+V2+V3)+41(V2+V3+V4+V5))=81(V0+V1+V4+V5)+41(V2+V3)
(3)计算边 E ( V 3 , V 2 ) E_{(V_3,V_2)} E(V3,V2) 的边点 e p ep ep:
e p = 1 2 ( e c + f p c ) = 1 2 ( 1 2 ( V 3 + V 2 ) + 1 8 ( V 0 + V 1 + V 4 + V 5 ) + 1 4 ( V 2 + V 3 ) ) = 1 16 ( V 0 + V 1 + V 4 + V 5 ) + 3 8 ( V 3 + V 2 ) \begin{aligned} ep&=\frac{1}{2}(ec+fpc)\\ &=\frac{1}{2}(\frac{1}{2}(V_3+V_2)+\frac{1}{8}(V_0+V_1+V_4+V_5)+\frac{1}{4}(V_2+V_3))\\ &=\frac{1}{16}(V_0+V_1+V_4+V_5)+\frac{3}{8}(V_3+V_2) \end{aligned} ep=21(ec+fpc)=21(21(V3+V2)+81(V0+V1+V4+V5)+41(V2+V3))=161(V0+V1+V4+V5)+83(V3+V2)
另,如果一条边只有一个相邻面 f f f,且该面面点为 f p fp fp 的话,那么第(2)步中计算 f p c fpc fpc 的公式则为:
f p c = 1 2 ( f p + f p ) fpc=\frac{1}{2}(fp+fp) fpc=21(fp+fp)
3. 计算平均面点(avg_face_points)
假设点 O O O 相邻的面有 f 1 , f 2 , f 3 , f 4 f_1,f_2,f_3,f_4 f1,f2,f3,f4 四个(实际不一定为4个相邻面),如下图所示(这四个正方形完全一样,所以最后计算出的 a v g f p avg_fp avgfp 与 O O O 重合):
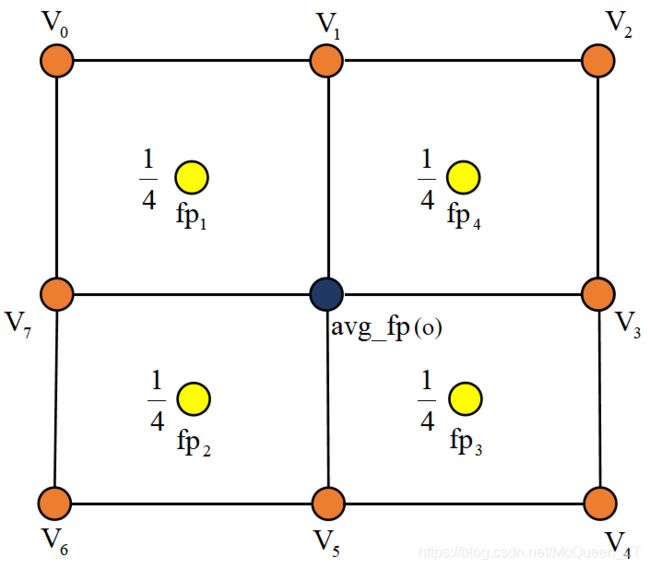
所以点 O O O 所有相邻面的平均面点 a v g _ f p avg\_fp avg_fp 的计算公式为:
a v g _ f p = 1 4 ( f p 1 + f p 2 + f p 3 + f p 4 ) avg\_fp=\frac{1}{4}(fp_1+fp_2+fp_3+fp_4) avg_fp=41(fp1+fp2+fp3+fp4)
4. 计算平均边中点(avg_mid_edges)
注意,这里计算的是平均边中点,而不是平均边点!
同样的,假设点 O ′ O' O′ 有四个相邻面,且这四个相邻面完全一致,如下图所示( a v g _ e c avg\_ec avg_ec 与 O ′ O' O′ 重合)
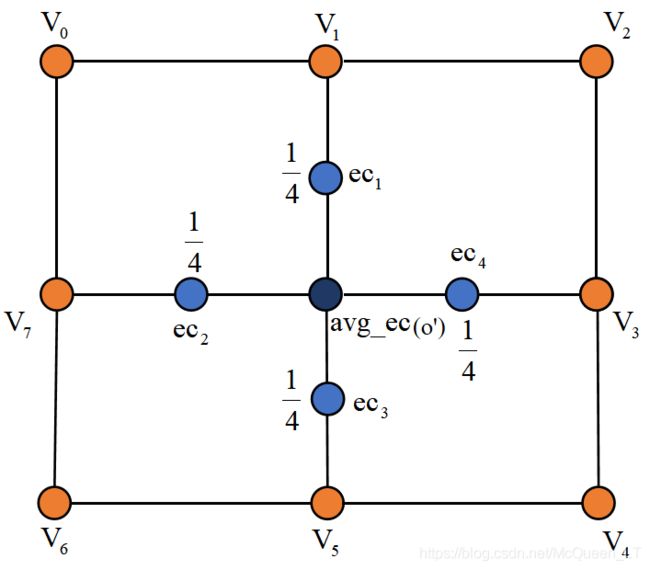
那么,计算 O ′ O' O′ 所有相邻边的平均边中点 a v g _ e c avg\_ec avg_ec 的计算公式为:
a v g _ e c = 1 4 ( e c 1 + e c 2 + e c 3 + e c 4 ) avg\_ec=\frac{1}{4}(ec_1+ec_2+ec_3+ec_4) avg_ec=41(ec1+ec2+ec3+ec4)
5. 更新原始点坐标
还是假设原始点 P P P 有四个相邻面,且更新后的点为 P ′ P' P′,则:
P ′ = 4 − α − β 4 ⋅ P + α 4 ⋅ a v g _ f p + β 4 ⋅ a v g _ e c P'= \frac{4-\alpha-\beta}{4}\cdot P+\frac{\alpha}{4}\cdot avg\_fp+\frac{\beta}{4}\cdot avg\_ec P′=44−α−β⋅P+4α⋅avg_fp+4β⋅avg_ec
本文中 α = 1 , β = 2 \alpha=1,\beta=2 α=1,β=2。
6. 插入新增点
新增的点就是之前计算得到的面点 f p fp fp 和边点 e p ep ep,
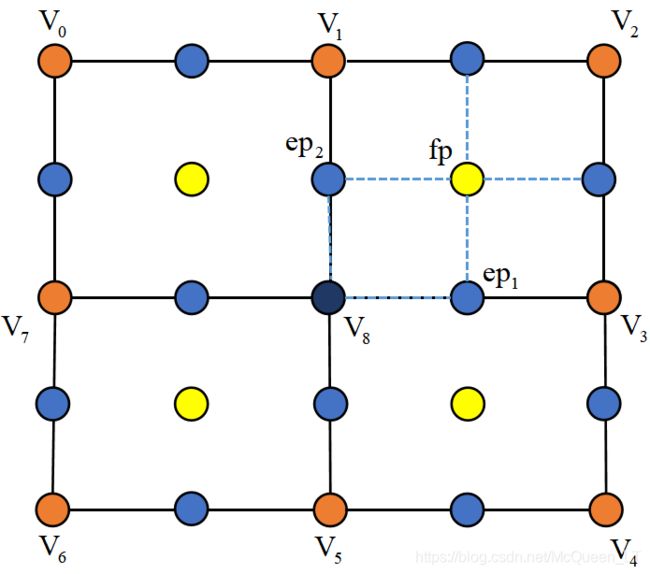
如上图所示, V 0 − V 8 V_0-V_8 V0−V8 所有的点均为更新之后的坐标,则对于面 f ( V 8 , V 3 , V 2 , V 1 ) f(V_8,V_3,V_2,V_1) f(V8,V3,V2,V1)得到新的面分别记为 f 1 , f 2 , f 4 , f 4 f_1,f_2,f_4,f_4 f1,f2,f4,f4,且 f 1 f_1 f1 构成为:
f 1 ( V 8 , e p 1 , f p , e p 2 ) f_1(V_8,ep_1,fp,ep_2) f1(V8,ep1,fp,ep2)
另外三个面同理。
三、示例效果
输入数据为一个立方体,包含八个顶点坐标,对其进行细分。
输入数据:

细分1次的结果:
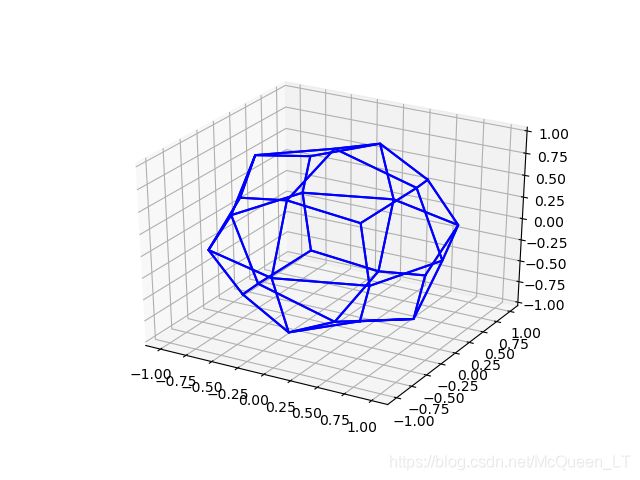
细分2次的结果:
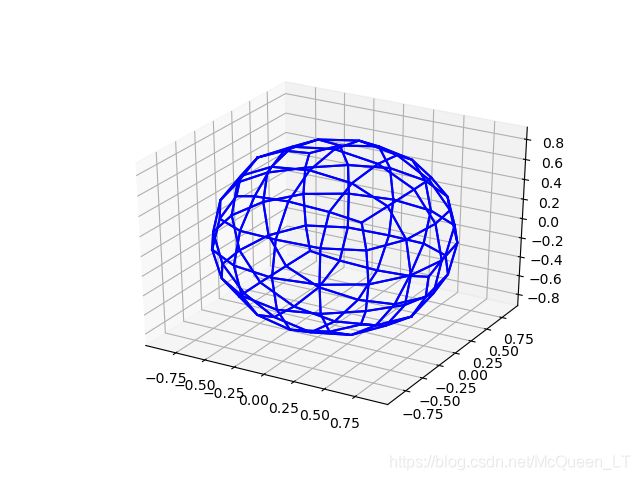
细分4次的结果:

四、完整代码
代码来源于Catmull–Clark subdivision surface,为了能够看到动态细分过程,我只修改了最后绘制部分的代码。
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
import numpy as np
import sys
import time
def center_point(p1, p2):
"""
returns a point in the center of the
segment ended by points p1 and p2
"""
cp = []
for i in range(3):
cp.append((p1[i] + p2[i]) / 2)
return cp
def sum_point(p1, p2):
"""
adds points p1 and p2
"""
sp = []
for i in range(3):
sp.append(p1[i] + p2[i])
return sp
def div_point(p, d):
"""
divide point p by d
"""
sp = []
for i in range(3):
sp.append(p[i] / d)
return sp
def mul_point(p, m):
"""
multiply point p by m
"""
sp = []
for i in range(3):
sp.append(p[i] * m)
return sp
def get_face_points(input_points, input_faces):
"""
From http://rosettacode.org/wiki/Catmull%E2%80%93Clark_subdivision_surface
1. for each face, a face point is created which is the average of all the points of the face.
"""
# 3 dimensional space
NUM_DIMENSIONS = 3
# face_points will have one point for each face
face_points = []
for curr_face in input_faces:
face_point = [0.0, 0.0, 0.0]
for curr_point_index in curr_face:
curr_point = input_points[curr_point_index]
# add curr_point to face_point
# will divide later
for i in range(NUM_DIMENSIONS):
face_point[i] += curr_point[i]
# divide by number of points for average
num_points = len(curr_face)
for i in range(NUM_DIMENSIONS):
face_point[i] /= num_points
face_points.append(face_point)
return face_points
def get_edges_faces(input_points, input_faces):
"""
Get list of edges and the one or two adjacent faces in a list.
also get center point of edge
Each edge would be [pointnum_1, pointnum_2, facenum_1, facenum_2, center]
"""
# will have [pointnum_1, pointnum_2, facenum]
edges = []
# get edges from each face
for facenum in range(len(input_faces)):
face = input_faces[facenum]
num_points = len(face)
# loop over index into face
for pointindex in range(num_points):
# if not last point then edge is curr point and next point
if pointindex < num_points - 1:
pointnum_1 = face[pointindex]
pointnum_2 = face[pointindex + 1]
else:
# for last point edge is curr point and first point
pointnum_1 = face[pointindex]
pointnum_2 = face[0]
# order points in edge by lowest point number
if pointnum_1 > pointnum_2:
temp = pointnum_1
pointnum_1 = pointnum_2
pointnum_2 = temp
edges.append([pointnum_1, pointnum_2, facenum])
# sort edges by pointnum_1, pointnum_2, facenum
edges = sorted(edges)
# merge edges with 2 adjacent faces
# [pointnum_1, pointnum_2, facenum_1, facenum_2] or
# [pointnum_1, pointnum_2, facenum_1, None]
num_edges = len(edges)
eindex = 0
merged_edges = []
while eindex < num_edges:
e1 = edges[eindex]
# check if not last edge
if eindex < num_edges - 1:
e2 = edges[eindex + 1]
if e1[0] == e2[0] and e1[1] == e2[1]:
merged_edges.append([e1[0], e1[1], e1[2], e2[2]])
eindex += 2
else:
merged_edges.append([e1[0], e1[1], e1[2], None])
eindex += 1
else:
merged_edges.append([e1[0], e1[1], e1[2], None])
eindex += 1
# add edge centers
edges_centers = []
for me in merged_edges:
p1 = input_points[me[0]]
p2 = input_points[me[1]]
cp = center_point(p1, p2)
edges_centers.append(me + [cp])
return edges_centers
def get_edge_points(input_points, edges_faces, face_points):
"""
for each edge, an edge point is created which is the average
between the center of the edge and the center of the segment made
with the face points of the two adjacent faces.
"""
edge_points = []
for edge in edges_faces:
# get center of edge
cp = edge[4]
# get center of two facepoints
fp1 = face_points[edge[2]]
# if not two faces just use one facepoint
# should not happen for solid like a cube
if edge[3] == None:
fp2 = fp1
else:
fp2 = face_points[edge[3]]
cfp = center_point(fp1, fp2)
# get average between center of edge and
# center of facepoints
edge_point = center_point(cp, cfp)
edge_points.append(edge_point)
return edge_points
def get_avg_face_points(input_points, input_faces, face_points):
"""
for each point calculate
the average of the face points of the faces the point belongs to (avg_face_points)
create a list of lists of two numbers [facepoint_sum, num_points] by going through the
points in all the faces.
then create the avg_face_points list of point by dividing point_sum (x, y, z) by num_points
"""
# initialize list with [[0.0, 0.0, 0.0], 0]
num_points = len(input_points)
temp_points = []
for pointnum in range(num_points):
temp_points.append([[0.0, 0.0, 0.0], 0])
# loop through faces updating temp_points
for facenum in range(len(input_faces)):
fp = face_points[facenum]
for pointnum in input_faces[facenum]:
tp = temp_points[pointnum][0]
temp_points[pointnum][0] = sum_point(tp, fp)
temp_points[pointnum][1] += 1
#以上统计每个点属于多少个面,并将每个面点求和,在接下来求平均
# divide to create avg_face_points
avg_face_points = []
for tp in temp_points:
afp = div_point(tp[0], tp[1])
avg_face_points.append(afp)
return avg_face_points
def get_avg_mid_edges(input_points, edges_faces):
"""
the average of the centers of edges the point belongs to (avg_mid_edges)
create list with entry for each point
each entry has two elements. one is a point that is the sum of the centers of the edges
and the other is the number of edges. after going through all edges divide by
number of edges.
"""
# initialize list with [[0.0, 0.0, 0.0], 0]
num_points = len(input_points)
temp_points = []
for pointnum in range(num_points):
temp_points.append([[0.0, 0.0, 0.0], 0])
# go through edges_faces using center updating each point
for edge in edges_faces:
cp = edge[4]
for pointnum in [edge[0], edge[1]]:
tp = temp_points[pointnum][0]
temp_points[pointnum][0] = sum_point(tp, cp)
temp_points[pointnum][1] += 1
# divide out number of points to get average
avg_mid_edges = []
for tp in temp_points:
ame = div_point(tp[0], tp[1])
avg_mid_edges.append(ame)
return avg_mid_edges
def get_points_faces(input_points, input_faces):
# initialize list with 0
num_points = len(input_points)
points_faces = []
for pointnum in range(num_points):
points_faces.append(0)
# loop through faces updating points_faces
for facenum in range(len(input_faces)):
for pointnum in input_faces[facenum]:
points_faces[pointnum] += 1
return points_faces
#统计每个点属于多少个面
def get_new_points(input_points, points_faces, avg_face_points, avg_mid_edges):
"""
m1 = (n - 3.0) / n
m2 = 1.0 / n
m3 = 2.0 / n
new_coords = (m1 * old_coords)
+ (m2 * avg_face_points)
+ (m3 * avg_mid_edges)
"""
new_points = []
for pointnum in range(len(input_points)):
n = points_faces[pointnum]
m1 = (n - 3.0) / n
m2 = 1.0 / n
m3 = 2.0 / n
old_coords = input_points[pointnum]
p1 = mul_point(old_coords, m1)
afp = avg_face_points[pointnum]
p2 = mul_point(afp, m2)
ame = avg_mid_edges[pointnum]
p3 = mul_point(ame, m3)
p4 = sum_point(p1, p2)
new_coords = sum_point(p4, p3)
new_points.append(new_coords)
return new_points
def switch_nums(point_nums):
"""
Returns tuple of point numbers
sorted least to most
"""
if point_nums[0] < point_nums[1]:
return point_nums
else:
return (point_nums[1], point_nums[0])
def cmc_subdiv(input_points, input_faces):
# 1. for each face, a face point is created which is the average of all the points of the face.
# each entry in the returned list is a point (x, y, z).
face_points = get_face_points(input_points, input_faces)
# get list of edges with 1 or 2 adjacent faces
# [pointnum_1, pointnum_2, facenum_1, facenum_2, center] or
# [pointnum_1, pointnum_2, facenum_1, None, center]
edges_faces = get_edges_faces(input_points, input_faces)
# get edge points, a list of points
edge_points = get_edge_points(input_points, edges_faces, face_points)
# the average of the face points of the faces the point belongs to (avg_face_points)
avg_face_points = get_avg_face_points(input_points, input_faces, face_points)
# the average of the centers of edges the point belongs to (avg_mid_edges)
avg_mid_edges = get_avg_mid_edges(input_points, edges_faces)
# how many faces a point belongs to
points_faces = get_points_faces(input_points, input_faces)
"""
m1 = (n - 3) / n
m2 = 1 / n
m3 = 2 / n
new_coords = (m1 * old_coords)
+ (m2 * avg_face_points)
+ (m3 * avg_mid_edges)
"""
new_points = get_new_points(input_points, points_faces, avg_face_points, avg_mid_edges)
"""
Then each face is replaced by new faces made with the new points,
for a triangle face (a,b,c):
(a, edge_point ab, face_point abc, edge_point ca)
(b, edge_point bc, face_point abc, edge_point ab)
(c, edge_point ca, face_point abc, edge_point bc)
for a quad face (a,b,c,d):
(a, edge_point ab, face_point abcd, edge_point da)
(b, edge_point bc, face_point abcd, edge_point ab)
(c, edge_point cd, face_point abcd, edge_point bc)
(d, edge_point da, face_point abcd, edge_point cd)
face_points is a list indexed by face number so that is
easy to get.
edge_points is a list indexed by the edge number
which is an index into edges_faces.
need to add face_points and edge points to
new_points and get index into each.
then create two new structures
face_point_nums - list indexes by facenum
whose value is the index into new_points
edge_point num - dictionary with key (pointnum_1, pointnum_2)
and value is index into new_points
"""
# add face points to new_points
face_point_nums = []
# point num after next append to new_points
next_pointnum = len(new_points)
for face_point in face_points:
new_points.append(face_point)
face_point_nums.append(next_pointnum)
next_pointnum += 1
# add edge points to new_points
edge_point_nums = dict()
for edgenum in range(len(edges_faces)):
pointnum_1 = edges_faces[edgenum][0]
pointnum_2 = edges_faces[edgenum][1]
edge_point = edge_points[edgenum]
new_points.append(edge_point)
edge_point_nums[(pointnum_1, pointnum_2)] = next_pointnum
next_pointnum += 1
# new_points now has the points to output. Need new
# faces
"""
just doing this case for now:
for a quad face (a,b,c,d):
(a, edge_point ab, face_point abcd, edge_point da)
(b, edge_point bc, face_point abcd, edge_point ab)
(c, edge_point cd, face_point abcd, edge_point bc)
(d, edge_point da, face_point abcd, edge_point cd)
new_faces will be a list of lists where the elements are like this:
[pointnum_1, pointnum_2, pointnum_3, pointnum_4]
"""
new_faces = []
for oldfacenum in range(len(input_faces)):
oldface = input_faces[oldfacenum]
# 4 point face
if len(oldface) == 4:
a = oldface[0]
b = oldface[1]
c = oldface[2]
d = oldface[3]
face_point_abcd = face_point_nums[oldfacenum]
edge_point_ab = edge_point_nums[switch_nums((a, b))]
edge_point_da = edge_point_nums[switch_nums((d, a))]
edge_point_bc = edge_point_nums[switch_nums((b, c))]
edge_point_cd = edge_point_nums[switch_nums((c, d))]
new_faces.append((a, edge_point_ab, face_point_abcd, edge_point_da))
new_faces.append((b, edge_point_bc, face_point_abcd, edge_point_ab))
new_faces.append((c, edge_point_cd, face_point_abcd, edge_point_bc))
new_faces.append((d, edge_point_da, face_point_abcd, edge_point_cd))
return new_points, new_faces
def graph_output(output_points, output_faces, fig):
ax = fig.add_subplot(111, projection='3d')
"""
Plot each face
"""
for facenum in range(len(output_faces)):
curr_face = output_faces[facenum]
xcurr = []
ycurr = []
zcurr = []
for pointnum in range(len(curr_face)):
xcurr.append(output_points[curr_face[pointnum]][0])
ycurr.append(output_points[curr_face[pointnum]][1])
zcurr.append(output_points[curr_face[pointnum]][2])
xcurr.append(output_points[curr_face[0]][0])
ycurr.append(output_points[curr_face[0]][1])
zcurr.append(output_points[curr_face[0]][2])
ax.plot(xcurr, ycurr, zcurr, color='b')
# cube
input_points = [
[-1.0, 1.0, 1.0],
[-1.0, -1.0, 1.0],
[1.0, -1.0, 1.0],
[1.0, 1.0, 1.0],
[1.0, -1.0, -1.0],
[1.0, 1.0, -1.0],
[-1.0, -1.0, -1.0],
[-1.0, 1.0, -1.0]
]
input_faces = [
[0, 1, 2, 3],
[3, 2, 4, 5],
[5, 4, 6, 7],
[7, 0, 3, 5],
[7, 6, 1, 0],
[6, 1, 2, 4],
]
iterations = 4
plt.ion()
output_points, output_faces = input_points, input_faces
for i in range(iterations):
output_points, output_faces = cmc_subdiv(output_points, output_faces)
fig = plt.figure(1)
plt.clf()
graph_output(output_points, output_faces, fig)
plt.pause(1)