A. Love Story
题意:找不同
思路:水
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
string st = "codeforces";
int main()
{
int t;cin >> t;
while(t--){
string str;cin >> str;
int num = 0;
for(int i = 0;i < 10;i++)
if(str[i] != st[i])
num++;
cout << num << endl;
}
}
B. Blank Space
题意:找最长连续0
思路:水
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
int main()
{
int t;cin >> t;
while(t--){
int n;cin >> n;
int num = 0,ma = 0;
for(int i = 1;i <= n;i++){
int x;cin >> x;
if(x == 0)
num++;
else
num = 0;
ma = max(ma,num);
}
cout << ma << endl;
}
}
C. Mr. Perfectly Fine
题意:需要两种特定技能,读书可以获得对于特定技能,每本书的成本不同,问最小需要多少花费才能学上这两种技能
思路:分两种情况,1.一本书有两个技能,2.两个技能分别归属于两本书,然后水
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
const int MAXN = 2e5 + 10;
int main()
{
int t;cin >> t;
while(t--){
int mil = 1e9,mir = 1e9,mi = 1e9;
int n;cin >> n;
fo(i,n){
int x;cin >> x;
string str;cin >> str;
if(str == "01")
mir = min(x,mir);
else if(str == "10")
mil = min(x,mil);
else if(str == "11")
mi = min(mi,x);
mi = min(mi,mil + mir);
}
if(mi == 1e9)
cout << -1 << endl;
else
cout << mi << endl;
}
}
D. Gold Rush
题意:一堆n个物品,一次操作可以分为大的一堆是小的一堆的两倍的两堆,问能否分出m个物品的堆
思路:小的一堆为 n / 3 n/3 n/3,大的为 2 n / 3 2n/3 2n/3,那么将n除3,如果比m小就乘2,然后2的数量不大于3的数量,直到n不能除3或相等为止,如果到最后都没找到,那么说明不能,否则可以
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 0;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
int main()
{
int t;cin >> t;
while(t--){
int n,m;cin >> n >> m;
if(m > n){
no;
continue;
}
bool f = 0;
int time = 0;
if(n == m)
f = 1;
while(n % 3 == 0){
n /= 3;
time++;
while(n < m && time){
time--;
n *= 2;
}
if(n == m)
f = 1;
}
if(n == m)
f = 1;
if(f)
yes;
else
no;
}
}
E. The Lakes
题意:找最大的相连的块
思路:dfs
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
const int MAXN = 1e3 + 10;
int a[MAXN][MAXN];
int n,m;
int now = 0;
void dfs(int i,int j){
if(!a[i][j])
return;
now += a[i][j];
a[i][j] = 0;
if(i + 1 <= n)
dfs(i + 1,j);
if(i - 1 >= 1)
dfs(i - 1,j);
if(j + 1 <= m)
dfs(i,j + 1);
if(j - 1 >= 1)
dfs(i,j - 1);
}
int main()
{
int t;cin >> t;
while(t--){
cin >> n >> m;
int ma = 0;
fo(i,n)fo(j,m) cin >> a[i][j];
fo(i,n)fo(j,m){
if(a[i][j]){
now = 0;
dfs(i,j);
ma = max(now,ma);
}
}
cout << ma << endl;
}
}
F. Forever Winter
题意:一个点连x个点,那x个点除初始点外还连着y个点,给出图,问x、y分别为多少(x,y均大于1)
对于初始点来说,有x条边与它相连,对于x个点来说,有y+1条边于其相连,一共还有xy个只有一条边的点,那么边数第二大的必定为y+1
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
const int MAXN = 1e3 + 10;
int num[MAXN];
int main()
{
int t;cin >> t;
while(t--){
int n,m;cin >> n >> m;
memset(num,0,sizeof(num));
fo(i,m){
int u,v;cin >> u >> v;
num[u]++;
num[v]++;
}
sort(num + 1,num + 1 + n);
int xy = 0;
fo(i,n) if(num[i] == 1) xy++;
cout << xy/(num[n-1]-1) << ' ' << num[n-1]-1 << endl;
}
}
G. Hits Different
题意:一个如图一样的塔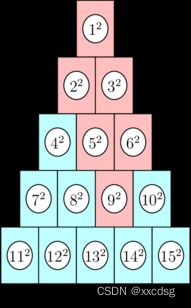
给出n,问n向上如图一样染色后所有被染色的方块的和
思路:n最大 1 0 6 10^6 106,那么找出所有的位置,然后向上一层一层加即可
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
const int MAXN = 1e6 + 10;
pair<int,int> pa[MAXN];
ll d[5000][5000];
ll f(int i,int l,int r){
ll ans = 0;
l = max(1,l),r = min(i,r);
for(int j = l;j <= r;j++)
ans += d[i][j];
if(i != 1)
ans += f(i - 1,l - 1,r);
return ans;
}
int main()
{
int t;cin >> t;
ll now = 1;
for(int i = 1;i <= 2000 && now < MAXN;i++)
for(int j = 1;j <= i && now < MAXN;j++){
d[i][j] = now*now;
pa[now] = {i,j};
now++;
}
while(t--){
ll n;cin >> n;
cout << f(pa[n].first,pa[n].second,pa[n].second) << endl;
}
}
H. Don’t Blame Me
题意:取子序列(取不同位置相同的数也不同),让其与和后有k位为1的取法
思路:容斥原理,至少k位为1的数量,减去至少k+1位为1的数量,加上…,因为范围较小,枚举所有可能的与的结果,还要乘上 C n u m k C_{num}^k Cnumk,代表加上或减去对于只有k位的情况
#include
using namespace std;
#define ll long long
#define lson(x) (1 << x)
#define rson(x) (1 << x | 1)
#define fo(i,n) for(int i = 1;i <= n;i++)
#define yes cout << "yes" << endl
#define no cout << "no" << endl
const int MAXN = 2e5 + 10,p = 1e9 + 7;
ll a[MAXN];
ll qpow(ll a,ll b){
ll ans = 1;
while(b){
if(b & 1) ans = (ans * a) % p;
a = (a * a) % p;
b >>= 1;
}
return ans;
}
ll ny[MAXN];
ll jcny[MAXN],jc[MAXN];
void pre_ny()
{
ny[1] = 1;
for(ll i = 2;i <= MAXN;i++)
ny[i] = ((p - p / i) * ny[p % i]) % p;
}
void pre_jcny()
{
jcny [0] = jcny[1] = 1;
for(ll i = 2;i <= MAXN;i++)
jcny[i] = jcny[i - 1] * ny[i] % p;
}
void pre_jc()
{
jc[0] = jc[1] = 1;
for(ll i = 2;i <= MAXN;i++)
jc[i] = jc[i - 1] * i % p;
}
ll C(ll a,ll b)
{
return (jc[a] * jcny[a - b] % p * jcny[b] % p) % p;
}
int main()
{
int t;cin >> t;
pre_ny();pre_jcny();pre_jc();
while(t--){
int n,k;cin >> n >> k;
fo(i,n) cin >> a[i];
ll ans = 0;
for(int i = 0;i <= 63;i++){
int op;
int ii = i,num = 0;
while(ii){
if(ii & 1) num++;
ii >>= 1;
}
if(num < k)
continue;
else if((num - k) % 2 == 0)
op = 1;
else
op = -1;
int nu = 0;
fo(j,n) if((i & a[j]) == i) nu++;
ans = (ans + (((qpow(2,nu) - 1)*op*(C(num,k))) % p) + p) % p;
}
cout << ans << endl;
}
}
