数字信号处理课程设计——调制与解调

文字目录

数字信号处理课程设计

摘要：

1绪论

1.1通信信号的调制与解调

1.2设计题目

2卷积定理和希尔伯特公式理论推导

2.1卷积定理

​2.2希尔伯特公式

3信号DSB调制与希尔伯特解调

3.1过程框图

3.2相关理论推导

3.2.1卷积定理在调制中的应用

3.2.2希尔伯特公式在解调中的应用

4仿真实现

4.1信号的产生

4.2信号的调制

4.3信号的解调

4.4时域图像绘制

4.5频域图像绘制

4.6解调信号绘制

5运行结果

5.1时域图像

5.2频域图像

 5.3解调信号

 5.4基带信号与解调信号的时域对比

 5.5基带信号与解调信号的频域对比

6结果分析

6.1调制结果分析

6.2解调结果分析

7总结

8参考文献

9附录

---

数字信号处理课程设计

摘要：

   在通信系统中，调制和解调是实现信号传输的关键步骤。为了将语音、音乐等信号发送到远方，发送端使用调制技术将信号的频谱转移到适合信道传输的较高频率范围。接收端通过解调将已调制的信号恢复到原来的频率范围，从而还原原始信号。调制和解调是通信系统设计中不可或缺的手段。

调制是将信号的频谱转移到较高频率范围的过程。通过调制，发送端将信号与较高频率的载波信号相乘，产生一个新的信号，其频谱位于较高频率范围。调制方式包括幅度调制和频率调制等。解调是恢复已调制信号的过程。接收端接收到已调制的信号后，使用相应的解调技术，将信号搬回原来的频率范围。解调过程与调制过程相反，通过希尔伯特变换，将信号的频谱还原到原始的频率范围，从而还原原始信号。

关键字：调制、解调、信号传输

1绪论

1.1通信信号的调制与解调

调制与解调是通信系统中的关键技术，用于在发送端将原始信号转换为适合传输的信号，以及在接收端将传输信号还原为原始信号。调制是将原始信号与高频载波信号进行相互作用，将信息转移到载波信号上的过程。解调则是从调制信号中提取出原始信息的过程。

调制技术可以分为模拟调制和数字调制两种类型。模拟调制适用于连续信号，常见的模拟调制技术有调幅（AM）、调频（FM）和调相（PM）等。数字调制则是将离散的数字信号转换为连续的调制信号，常见的数字调制技术有脉冲编码调制（PCM）、相移键控调制（PSK）、正交幅度调制（QAM）等。

解调过程则是将调制信号转换回原始信号的过程。解调技术与调制技术相对应，通常采用相应的解调器进行实现。解调器根据调制信号的特征，采用相应的算法和电路，将调制信号还原为原始信号。

调制与解调技术的发展对通信系统的性能和效率起着至关重要的作用。通过合理选择调制方式和解调算法，可以实现高速率、低误码率和抗干扰能力强的通信系统。同时，调制与解调技术在无线通信、数字电视、调制解调器等领域都有广泛的应用。

随着通信技术的不断发展，调制与解调技术也在不断演进。新的调制与解调方案不断涌现，以满足日益增长的通信需求。同时，软件无线电（SDR）等新兴技术的出现，也为调制解调技术的研究和应用带来了新的机遇和挑战。

1.2设计题目

2卷积定理和希尔伯特公式理论推导

2.1卷积定理

时域的乘积的傅里叶变换等于频域卷积乘以1/2π ，即

F[f1⋅f2]=1/2πF[f1]* F[f2]

证明：设F1(ω)=F[f1(t)],F2(ω)=F[f2(t)] ，F-1 表示傅里叶逆变换，则

2.2希尔伯特公式

函数ut 的希尔伯特变换定义为：

H(u)(t)=u*h=1/πp⋅v⋅∫-∞+∞u(τ)/t-τdτ

举个例子，计算coswt 的希尔伯特变换:

这表明希尔伯特变换让原信号所有频率分量相位推迟90度。

3信号DSB调制与希尔伯特解调

3.1过程框图

3.2相关理论推导

3.2.1卷积定理在调制中的应用

在信号处理和通信领域中，频域卷积和调制是常见的操作。让我们逐步解释相关概念，并探讨它们之间的关系。

调制是一种在信号中加入调制信号的过程。这通常涉及将待调制信号乘以调制信号，以便在频域上进行频谱的移动或变换。在调制中，调制信号通常是一个正弦函数或复指数函数。

调制可以用频域的观点来解释。假设有一个信号ct 和一个调制信号st ，我们可以将它们的傅里叶变换表示为Cw 和Sw 。如果我们将ct 乘以st ，得到信号mt=st⋅ct 。根据频域的性质，我们知道它对应的频谱为 M(ω) = 1/2π · S(ω) * C(ω)。这意味着在频域中，将信号的频谱和调制信号的频谱进行卷积，并乘以一个常数12π 。

因此，在调制中，将信号乘以调制信号可以看作是对信号频谱进行卷积运算，并乘以一个常数。这样的操作可用于频谱移动、频率调制、调幅调频等应用中，以实现信号的调制和解调。

需要注意的是，上述描述是基于频域观点的简化解释，并不考虑时域的因果性和实际实现的复杂性。在实际应用中，需要进行适当的滤波和频谱处理，以确保信号的正确调制和解调。

3.2.2希尔伯特公式在解调中的应用

希尔伯特公式在信号处理中被广泛应用于解调和分析复杂信号。该公式可以用于生成信号的解析信号，进而提取出原始信号的振幅和相位信息。

希尔伯特公式指出，对于一个实值信号 x(t)，可以通过将其与希尔伯特变换滤波器的输出相加，得到对应的解析信号。解析信号是一个复值信号，其中实部是原始信号 x(t)，而虚部是原始信号的希尔伯特变换。

解析信号可以用以下公式表示：

z(t) = x(t) + j * H[x(t)]

其中，z(t) 是解析信号，x(t) 是原始信号，j 是虚数单位，H[ ] 表示希尔伯特变换操作。

生成解析信号后，可以通过提取解析信号的幅度来进行解调。解析信号的幅度表示了原始信号的振幅信息，可以用于提取所需的调制信号或消息信号。

解析信号的幅度可以通过以下公式计算：

A(t) = |z(t)|

其中，A(t) 表示解析信号的幅度。

通过计算解析信号的幅度，可以实现解调操作，提取原始信号的振幅信息。这在调制解调、通信系统和信号分析中具有广泛的应用。

需要注意的是，希尔伯特变换和解析信号的计算可能需要使用数字信号处理技术或相关算法进行实现。在实际应用中，可以使用离散时间的希尔伯特变换（discrete-time Hilbert transform）或基于数字滤波器的方法来实现希尔伯特变换和解析信号的计算。

4仿真实现

4.1信号的产生

Fs = 2048
t = np.arange(-0.5, 0.5, 1/Fs)
s = np.sinc(50*t)**2
N = len(t)
f = 250
c = np.cos(2*np.pi*f*t)

4.2信号的调制

# 卷积定理调制（DSB调制）
m = s * c

4.3信号的解调

# 卷积定理解调
# x = m * c
# HIBERT解调
h = hilbert(m)  # 利用希尔伯特变换得到解析信号
x = np.abs(h)   # 计算解析信号的幅度值

4.4时域图像绘制

# 时域图像
plt.figure(1)
# 基带信号
plt.subplot(3, 1, 1)
plt.plot(t, s)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('基带信号')
# 载波信号
plt.subplot(3, 1, 2)
plt.plot(t, c)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('载波信号')
# 调制信号
plt.subplot(3, 1, 3)
plt.plot(t, m)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('调制信号')

4.5频域图像绘制

# 频域图像
plt.figure(2)
plt.subplot(3, 1, 1) # 基带信号
f = np.fft.fftshift(np.fft.fftfreq(N, 1/Fs))
S = np.fft.fftshift(np.abs(np.fft.fft(s)))
plt.plot(f, S)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('基带信号频域')
# 载波信号
plt.subplot(3, 1, 2)
M = np.fft.fftshift(np.abs(np.fft.fft(c)))
plt.plot(f, M)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('载波信号频域')
# 调制信号
plt.subplot(3, 1, 3)
M = np.fft.fftshift(np.abs(np.fft.fft(m)))
plt.plot(f, M)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('调制信号频域')

4.6解调信号绘制

plt.figure(3)
# 时域图像
plt.subplot(2, 1, 1)
plt.plot(t, x)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('解调信号时域图像')
# 频域图像
plt.subplot(2, 1, 2)
X = np.fft.fftshift(np.abs(np.fft.fft(x)))
plt.plot(f, X)
plt.xlabel('频率 (Hz)')
plt.ylabel('波幅')
plt.title('解调信号频域图像')

5运行结果

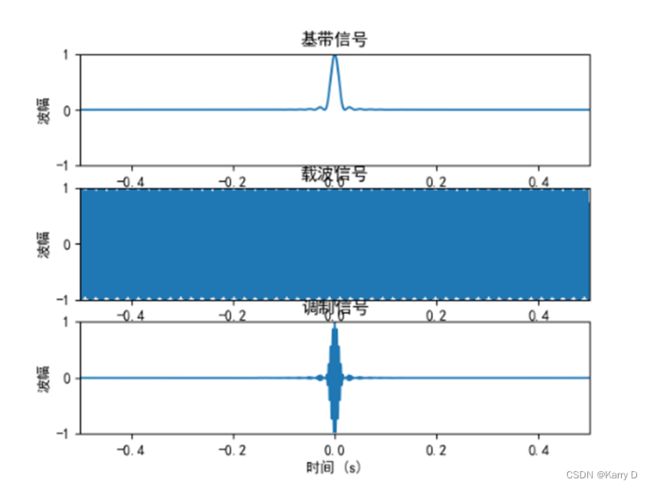
5.1时域图像

5.2频域图像

 5.3解调信号

 5.4基带信号与解调信号的时域对比

 5.5基带信号与解调信号的频域对比

6结果分析

6.1调制结果分析

DSB调制是一种常见的调制技术，其原理是将待调制信号与载波信号相乘，得到双边带调制信号。

从频域图像中可以看出，DSB调制的频谱是原始信号频谱的两个副本，分别位于正频率和负频率。频谱的幅度表示了信号的强度或能量。当进行DSB调制后，频域图像中的幅度会变为原来的一半。这是因为在DSB调制中，将原始信号与载波信号相乘会导致频谱的幅度减半。

6.2解调结果分析

希尔伯特解调是一种通过希尔伯特变换将调制信号转换为复数信号，并计算其幅度以还原基带信号的方法。它在信号处理和通信系统中起着重要的作用，可以用于恢复原始信号以及分析信号的频谱特性。

通过希尔伯特变换成功地解调出了基带信号，并通过对比图像以及编程实现验证了整个过程的成功。这表明希尔伯特解调和相关的编程实现是有效的，可在信号处理和通信系统中应用。

7总结

本次课程设计主要涉及通信信号卷积定理、调制和希尔伯特公式在信号处理中的应用。通过对这些概念的学习和实践，我对信号处理和通信系统的原理有了更深入的理解。

在报告中，我首先介绍了通信信号卷积定理，它说明了在频域中进行卷积运算等效于在时域中进行乘积运算。这个定理对于分析和设计滤波器、调制和解调等任务非常有用。

接下来，我详细讨论了调制的概念和应用。调制是一种在信号中引入调制信号的过程，可以实现频谱的移动和信号的编码。我解释了调制的原理以及调制解调过程。

最后，我探讨了希尔伯特公式在解调中的应用。希尔伯特公式可以用于生成信号的解析信号，从中提取振幅和相位信息。通过解析信号的幅度，可以实现解调操作，提取原始信号的相关信息。

通过这个课程设计，我对信号处理和通信系统的关键概念有了更深入的了解。我学会了如何利用卷积定理进行频域分析和设计滤波器。我也理解了调制的原理和应用，以及希尔伯特公式在解调中的重要性。

这个课程设计还帮助我提高了实践能力。我使用编程工具和相关算法实现了卷积、调制和希尔伯特变换，并进行了信号处理和解调的实验。这些实验不仅加深了我对理论知识的理解，还提供了实际问题解决的经验。

总的来说，这个课程设计为我提供了一个全面的学习和实践平台，使我能够深入了解通信信号卷积定理、调制和希尔伯特公式在信号处理中的应用。通过这个过程，我获得了宝贵的知识和技能，为未来的学习和职业发展奠定了坚实的基础。

8参考文献

【1】张建功, 朱虹, 张维明. (2019). 信号处理基础与应用. 清华大学出版社.

【2】王华, 郭令宾, 胡迅. (2017). 数字通信系统原理与应用. 电子工业出版社.

【3】张晨光, 张维明, 王梦婷. (2018). 调制解调原理与应用. 电子工业出版社.

【4】李华, 金良志, 殷方红. (2015). 数字信号处理教程（第四版）. 电子工业出版社.

【5】刘伟明, 谢世茂. (2014). 通信原理与系统仿真. 高等教育出版社.

【6】熊秉明, 梁青, 马少平. (2016). 数字信号处理与系统设计. 机械工业出版社.

【7】陈大松, 郭丽燕, 李峰. (2017). 基于希尔伯特变换的分析方法及其应用. 电子技术与软件工程, 16(6), 33-34.

【8】郑云龙, 王瑞娟. (2017). 希尔伯特变换在故障诊断中的应用研究. 传感器与微系统, 36(2), 111-115.

【9】孙璟, 陈秋荣, 郭晓宇. (2020). 基于希尔伯特变换的混凝土缺陷声发射检测方法研究. 声学技术, 39(3), 259-263.

【10】李冬梅, 王东. (2021). 基于希尔伯特变换的心电信号分析方法研究. 生物医学工程与临床, 25(1), 9-13.

9附录

完整代码：
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import hilbert
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
plt.rcParams['font.sans-serif'] = ['SimHei']
Fs = 2048
t = np.arange(-0.5, 0.5, 1/Fs)
s = np.sinc(50*t)**2
N = len(t)
f = 250
c = np.cos(2*np.pi*f*t)
# 卷积定理调制（DSB调制）
m = s * c
# 时域图像
plt.figure(1)
# 基带信号
plt.subplot(3, 1, 1)
plt.plot(t, s)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('基带信号')
# 载波信号
plt.subplot(3, 1, 2)
plt.plot(t, c)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('载波信号')
# 调制信号
plt.subplot(3, 1, 3)
plt.plot(t, m)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('调制信号')
# 频域图像
plt.figure(2)
# 基带信号
plt.subplot(3, 1, 1)
f = np.fft.fftshift(np.fft.fftfreq(N, 1/Fs))
S = np.fft.fftshift(np.abs(np.fft.fft(s)))
plt.plot(f, S)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('基带信号频域')
# 载波信号
plt.subplot(3, 1, 2)
M = np.fft.fftshift(np.abs(np.fft.fft(c)))
plt.plot(f, M)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('载波信号频域')
# 调制信号
plt.subplot(3, 1, 3)
M = np.fft.fftshift(np.abs(np.fft.fft(m)))
plt.plot(f, M)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('调制信号频域')
plt.show()
# 卷积定理解调
# x = m * c
# HIBERT解调
h = hilbert(m)  # 利用希尔伯特变换得到解析信号
x = np.abs(h)   # 计算解析信号的幅度值
plt.figure(3)
# 时域图像
plt.subplot(2, 1, 1)
plt.plot(t, x)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('解调信号时域图像')
# 频域图像
plt.subplot(2, 1, 2)
X = np.fft.fftshift(np.abs(np.fft.fft(x)))
plt.plot(f, X)
plt.xlabel('频率 (Hz)')
plt.ylabel('波幅')
plt.title('解调信号频域图像')
plt.figure(4)
# 基带信号
plt.subplot(2, 1, 1)
plt.plot(t, s)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('基带信号')
# 时域图像
plt.subplot(2, 1, 2)
plt.plot(t, x)
plt.axis([-0.5, 0.5, -1.0, 1.0])
plt.xlabel('时间 (s)')
plt.ylabel('波幅')
plt.title('解调信号时域图像')
plt.figure(5)
# 基带信号
plt.subplot(2, 1, 1)
plt.plot(f, S)
plt.xlabel('频率(Hz)')
plt.ylabel('波幅')
plt.title('基带信号频域')
# 频域图像
plt.subplot(2, 1, 2)
X = np.fft.fftshift(np.abs(np.fft.fft(x)))
plt.plot(f, X)
plt.xlabel('频率 (Hz)')
plt.ylabel('波幅')
plt.title('解调信号频域图像')
plt.show()