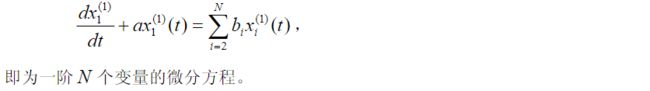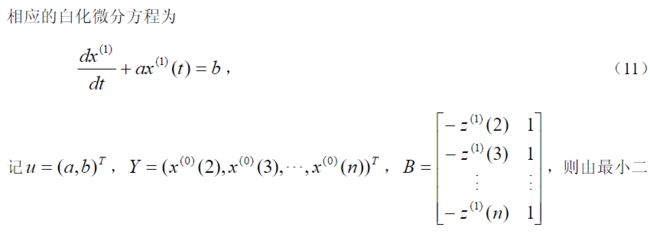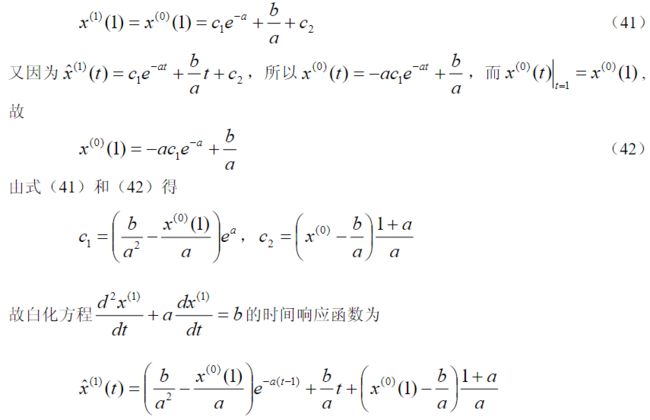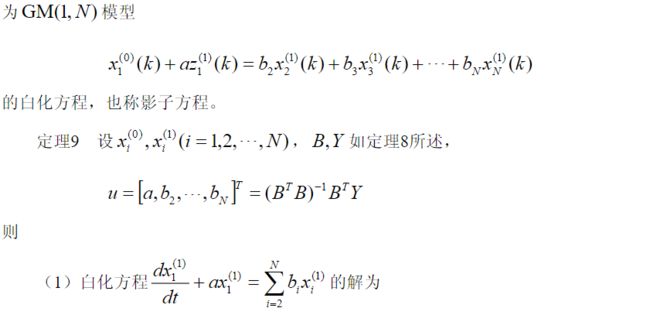灰色系统理论及其应用

灰色系统理论及其应用

客观世界的很多实际问题，其内部的结构、参数以及特征并未全部被人们了解，人们不可能象研究白箱问题那样将其内部机理研究清楚，只能依据某种思维逻辑与推断来构造模型。对这类部分信息已知而部分信息未知的系统，我们称之为灰色系统。本章介绍的方法是从灰色系统的本征灰色出发，研究在信息大量缺乏或紊乱的情况下，如何对实际问题进行分析和解决。

1. 灰色系统概论

客观世界在不断发展变化的同时，往往通过事物之间及因素之间相互制约、相互联系而构成一个整体，我们称之为系统。按事物内涵的不同，人们已建立了工程技术、社会系统、经济系统等。人们试图对各种系统所外露出的一些特征进行分析，从而弄清楚系统内部的运行机理。从信息的完备性与模型的构建上看，工程技术等系统具有较充足的信息量，其发展变化规律明显，定量描述较方便，结构与参数较具体，人们称之为白色系统；对另一类系统诸如社会系统、农业系统、生态系统等，人们无法建立客观的物理原型，其作用原理亦不明确，内部因素难以辨识或之间关系隐蔽，人们很难准确了解这类系统的行为特征，因此对其定量描述难度较大，带来建立模型的困难。这类系统内部特性部分已知的系统称之为灰色系统。一个系统的内部特性全部未知，则称之为黑色系统。

区别白色系统与灰色系统的重要标志是系统内各因素之间是否具有确定的关系。运动学中物体运动的速度、加速度与其所受到的外力有关，其关系可用牛顿定律以明确的定量来阐明，因此，物体的运动便是一个白色系统。

当然，白、灰、黑是相对于一定的认识层次而言的，因而具有相对性。某人有一天去他朋友家做客，发现当外面的汽车开过来时，他朋友家的狗就躲到屋角里瑟瑟发抖。他对此莫名其妙。但对他朋友来讲，狗的这种行为是可以理解的，因为他知道，狗在前不久曾被汽车撞伤过。显然，同样对于“狗的惧怕行为”，客人因不知内情而面临一个黑箱，而主人则面临一个灰箱。

作为实际问题，灰色系统在大千世界中是大量存在的，绝对的白色或黑色系统是很少的。随着人类认识的进步及对掌握现实世界的要求的升级，人们对社会、经济等问题的研究往往已不满足于定性分析。尽管当代科技日新月异，发展迅速，但人们对自然界的认识仍然是肤浅的。粮食作物的生产是一个实际的关系到人们吃饭的大问题，但同时，它又是一个抽象的灰色系统。肥料、种子、农药、气象、土壤、劳力、水利、耕作及政策等皆是影响生产的因素，但又难以确定影响生产的确定因素，更难确定这些因素与粮食产量的定量关系。人们只能在一定的假设条件（往往是一些经验及常识）下按照某种逻辑推理演绎而得到模型。这种模型并非是粮食作物生产问题在理论认识上的“翻版”，而只能看作是人们在认识上对实际问题的一种==“反映”或“逼近”==。

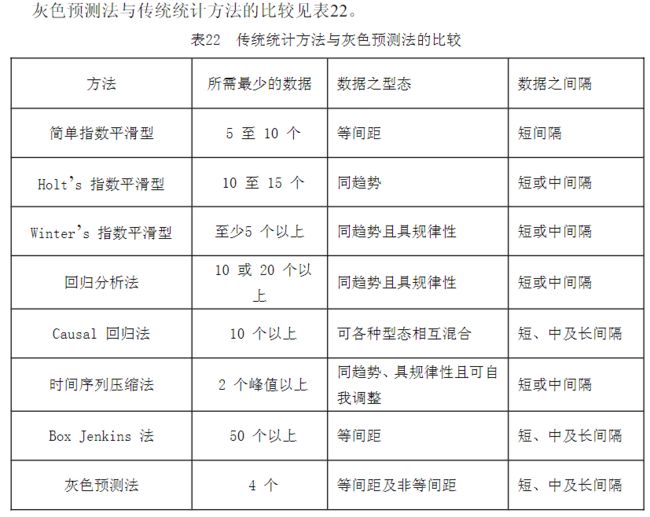
社会、经济、农业以及生态系统一般都会有不可忽略的“噪声”（即随即干扰）。现有的研究经常被“噪声”污染。受随机干扰侵蚀的系统理论主要立足于概率统计。通过统计规律、概率分布对事物的发展进行预测，对事物的处置进行决策。现有的系统分析的量化方法，大都是数理统计法如回归分析、方差分析、主成分分析等，回归分析是应用最广泛的一种办法。但回归分析要求大样本，只有通过大量的数据才能得到量化的规律，这对很多无法得到或一时缺乏数据的实际问题的解决带来困难。回归分析还要求样本有较好的分布规律，而很多实际情形并非如此。例如，我国建国以来经济方面有几次大起大落，难以满足样本有较规律的分布要求。因此，有了大量的数据也不一定能得到统计规律，甚至即使得到了统计规律，也并非任何情况都可以分析。另外，回归分析不能分析因素间动态的关联程度，即使是静态，其精度也不高，且常常出现反常现象。

灰色系统理论提出了一种新的分析方法—关联度分析方法，即根据因素之间发展态势的相似或相异程度来衡量因素间关联的程度，它揭示了事物动态关联的特征与程度。由于以发展态势为立足点，因此对样本量的多少没有过分的要求，也不需要典型的分布规律，计算量少到甚至可用手算，且不致出现关联度的量化结果与定性分析不一致的情况。这种方法已应用到农业经济、水利、宏观经济等各方面，都取得了较好的效果。灰色系统理论建模的主要任务是根据具体灰色系统的行为特征数据，充分开发并利用不多的数据中的显信息和隐信息，寻找因素间或因素本身的数学关系。通常的办法是采用离散模型，建立一个按时间作逐段分析的模型。但是，离散模型只能对客观系统的发展做短期分析，适应不了从现在起做较长远的分析、规划、决策的要求。尽管连续系统的离散近似模型对许多工程应用来讲是有用的，但在某些研究领域中，人们却常常希望使用微分方程模型。事实上，微分方程的系统描述了我们所希望辨识的系统内部的物理或化学过程的本质。

灰色系统理论首先基于对客观系统的新的认识。尽管某些系统的信息不够充分，但作为系统必然是有特定功能和有序的，只是其内在规律并未充分外露。有些随机量、无规则的干扰成分以及杂乱无章的数据列，从灰色系统的观点看，并不认为是不可捉摸的。相反地，灰色系统理论将随机量看作是在一定范围内变化的灰色量，按适当的办法将原始数据进行处理，将灰色数变换为生成数，从生成数进而得到规律性较强的生成函数。例如，某些系统的数据经处理后呈现出指数规律，这是由于大多数系统都是广义的能量系统，而指数规律是能量变化的一种规律。灰色系统理论的量化基础是生成数，从而突破了概率统计的局限性，使其结果不再是过去依据大量数据得到的经验性的统计规律，而是现实性的生成律。这种使灰色系统变得尽量清晰明了的过程被称为白化。

目前，灰色系统理论已成功地应用于工程控制、经济管理、未来学研究、生态系统及复杂多变的农业系统中，并取得了可喜的成就。灰色系统理论有可能对社会、经济等抽象系统进行分析、建模、预测、决策和控制，它有可能成为人们认识客观系统改造客观系统的一个新型的理论工具。

2. 关联分析

大千世界里的客观事物往往现象复杂，因素繁多。我们往往需要对系统进行因素分析，这些因素中哪些对系统来讲是主要的，哪些是次要的哪些需要发展，哪些需要抑制，哪些是潜在的，哪些是明显的。一般来讲，这些都是我们极为关心的问题。事实上，因素间关联性如何、关联程度如何量化等问题是系统分析的关键和起点。

因素分析的基本方法过去主要采取回归分析等办法。正如前一节指出的，回归分析的办法有很多欠缺，如要求大量数据、计算量大及可能出现反常情况等。为克服以上弊病，本节采用关联度分析的办法来做系统分析。

作为一个发展变化的系统，关联分析实际上是动态过程发展态势的量化比较分析。所谓发展态势比较，也就是系统各时期有关统计数据的几何关系的比较。
例如，某地区 1977～1983 年总收入与养猪、养兔收入资料见表 1。
表 1 收入数据

根据表 1，做曲线图 1。

图 1 收入数据图

由上图易看出，曲线 A 与曲线 B 发展趋势比较接近，而与曲线 C 相差较大，因此可以判断，该地区对总收入影响较直接的是养猪业，而不是养兔业。很显然，几何形状越接近，关联程度也就越大。当然，直观分析对于稍微复杂些的问题则显得难于进行。因此，需要给出一种计算方法来衡量因素间关联程度的大小。

2.1 数据变换技术
为保证建模的质量与系统分析的正确结果，对收集来的原始数据必须进行数据变换和处理，使其消除量纲和具有可比性。
定义 1 设有序列则称映射

为序列 x 到序列 y 的数据变换。
1）当

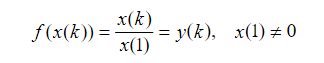
称 f 是初值化变换。
2）当

称 f 是均值化变换。
3）当

称 f 是百分比变换。

4）当

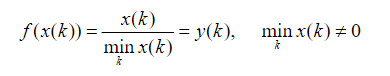
称 f 是倍数变换。
5）当

其中x0 为大于零的某个值，称 f 是归一化变换。
6)当

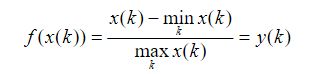
称f 是极差最大值化变换。
7）当

称 f 是区间值化变换。
2.2 关联分析
定义 2 选取参考数列

其中 k 表示时刻。假设有 m 个比较数列

则称

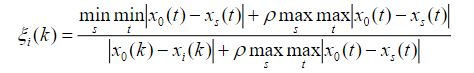
为比较数列xi 对参考数列 x0 在 k 时刻的关联系数，其中ρ∈[0,1]
为分辨系数。称式中
分别为两级最小差及两级最大差。
一般来讲，分辨系数ρ 越大，分辨率越大；ρ 越小，分辨率越小。
（1）式定义的关联系数是描述比较数列与参考数列在某时刻关联程度的一种指标，由于各个时刻都有一个关联数，因此信息显得过于分散，不便于比较，为此我们给出
定义 3 称

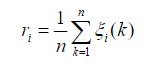
为数列 xi 对参考数列 x0 的关联度。
由（2）易看出，关联度是把各个时刻的关联系数集中为一个平均值，亦即把过于分散的信息集中处理。利用关联度这个概念，我们可以对各种问题进行因素分析。考虑下面的问题。
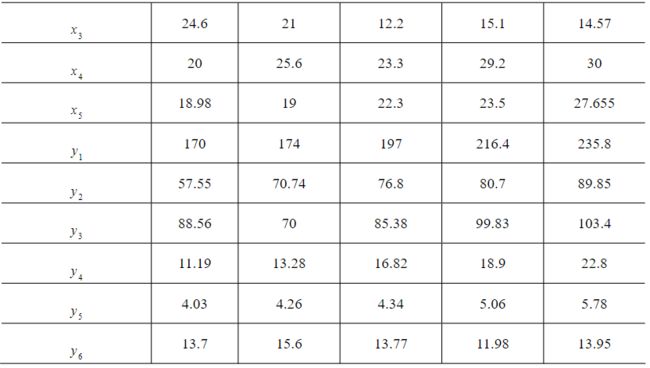
例 1 通过对某健将级女子铅球运动员的跟踪调查，获得其 1982 年至 1986 年每年最好成绩及 16 项专项素质和身体素质的时间序列资料，见表 2，试对此铅球运动员的专项成绩进行因素分析。
表 2 各项成绩数据

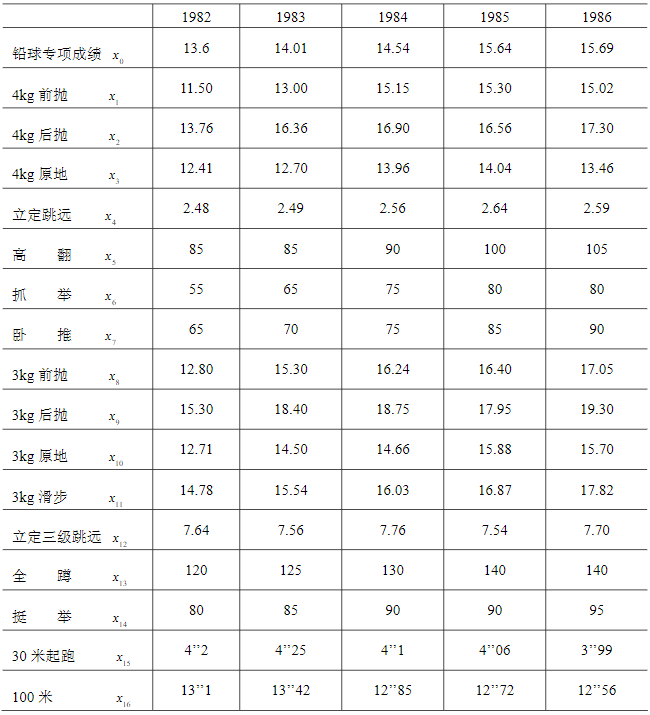
在利用（1）式及（2）式计算关联度之前，我们需对表 2 的各个数列做初始化处理。一般来讲，实际问题中的不同数列往往具有不同的量纲，而我们在计算关联系数时，要求量纲要相同。因此，需首先对各种数据进行无量纲化。另外，为了易于比较，要求所有数列有公共的交点。为了解决上述两个问题，我们对给定数列进行变换。
定义 4 给定数列x=(x(1),x(2),…,下（n))，称

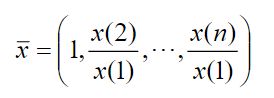
为原始数列 X 的初始化数列。
这样，我们可对表 2 中的 17 个数列进行初始化处理。注意，对于前 15 个数列，随着时间的增加，数值的增加意味着运动水平的进步，而对后 2 个数列来讲，随着时间的增加，数值（秒数）的减少却意味着运动水平的进步。因此，在对数列 15x 及 16x 进行初始化处理时，采取以下公式

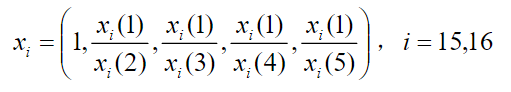
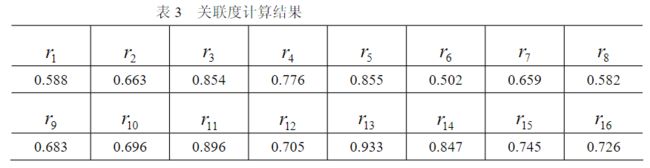
依照问题的要求，我们自然选取铅球运动员专项成绩作为参考数列，将表 2 中的各个数列的初始化数列代入（1）及（2）式，易算出各数列的关联度如下表（这里ρ=5.0 ）。

clc,clear
load x.txt %把原始数据存放在纯文本文件 x.txt 中
for i=1:15
x(i,:)=x(i,:)/x(i,1); %标准化数据
end
for i=16:17
x(i,:)=x(i,1)./x(i,:); %标准化数据
end
data=x;
n=size(data,1);
ck=data(1,:);m1=size(ck,1);
bj=data(2:n,:);m2=size(bj,1);
for i=1:m1
for j=1:m2
t(j,:)=bj(j,:)-ck(i,:);
end
jc1=min(min(abs(t')));jc2=max(max(abs(t')));
rho=0.5;
ksi=(jc1+rho*jc2)./(abs(t)+rho*jc2);
rt=sum(ksi')/size(ksi,2);
r(i,:)=rt;
end
r
[rs,rind]=sort(r,'descend') %对关联度进行排序

由表 3 易看出，影响铅球专项成绩的前八项主要因素依次为全蹲、3kg 滑步、高翻、4kg 原地、挺举、立定跳远、30 米起跳、100 米成绩。因此，在训练中应着重考虑安排这八项指标的练习。这样可减少训练的盲目性，提高训练效果。
应该指出的是，公式（1）中的 |)()(| 0 kxkx i− 不能区别因素关联是正关联还是负关联，可采取下述办法解决这个问题。记

3.优势分析

根据表 4 的数据，利用如下的 MATLAB 程序

clc,clear
load data.txt %把原始数据存放在纯文本文件 data.txt 中
n=size(data,1);
for i=1:n
data(i,:)=data(i,:)/data(i,1); %标准化数据
end
ck=data(6:n,:);m1=size(ck,1);
bj=data(1:5,:);m2=size(bj,1);
for i=1:m1
for j=1:m2
t(j,:)=bj(j,:)-ck(i,:);
end
jc1=min(min(abs(t')));jc2=max(max(abs(t')));
rho=0.5;
ksi=(jc1+rho*jc2)./(abs(t)+rho*jc2);
rt=sum(ksi')/size(ksi,2);
r(i,:)=rt;
end
r

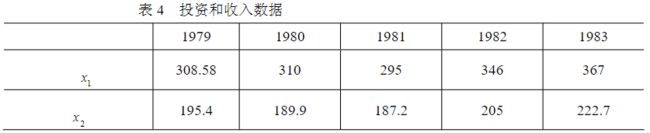
计算出各个子因素对母因素的关联度（这里取 ρ=0.5 ），从而得到关联矩阵为

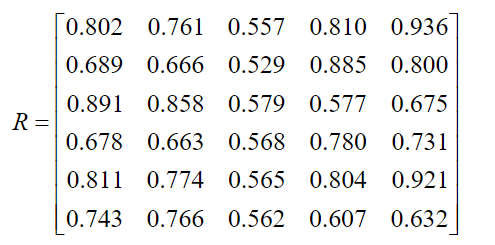
4.生成树

5.灰色模型GM

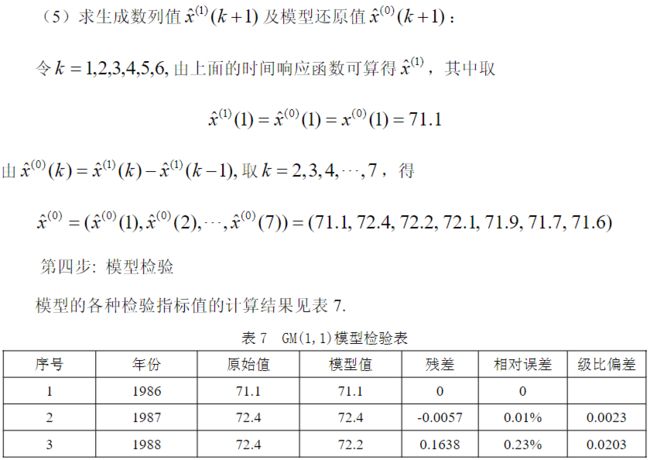
6.灰色预测

clc,clear
a=[390.6,412,320,559.2,
380.8,542.4,553,310,561,300,632,540,406.2,313.8,576,587.6,318.5]'
;
t0=find(a<=320);
t1=cumsum(t0);n=length(t1);
B=[-0.5*(t1(1:end-1)+t1(2:end)),ones(n-1,1)];Y=t0(2:end);
r=B\Y
y=dsolve('Dy+a*y=b','y(0)=y0');
y=subs(y,{'a','b','y0'},{r(1),r(2),t1(1)});
yuce1=subs(y,'t',[0:n+1])
digits(6),y=vpa(y) %为提高预测精度，先计算预测值，再显示微分方程的解
yuce=diff(yuce1);
yuce=[t0(1),yuce]

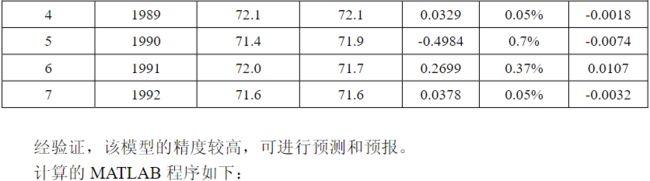
clc,clear
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n=length(x0);
lamda=x0(1:n-1)./x0(2:n)
range=minmax(lamda)
x1=cumsum(x0)
for i=2:n
z(i)=0.5*(x1(i)+x1(i-1));
end
B=[-z(2:n)',ones(n-1,1)];
Y=x0(2:n)';
u=B\Y
x=dsolve('Dx+a*x=b','x(0)=x0');
x=subs(x,{'a','b','x0'},{u(1),u(2),x1(1)});
yuce1=subs(x,'t',[0:n-1]);
digits(6),y=vpa(x) %为提高预测精度，先计算预测值，再显示微分方程的解
yuce=[x0(1),diff(yuce1)]
epsilon=x0-yuce %计算残差
delta=abs(epsilon./x0) %计算相对误差
rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda %计算级比偏差值

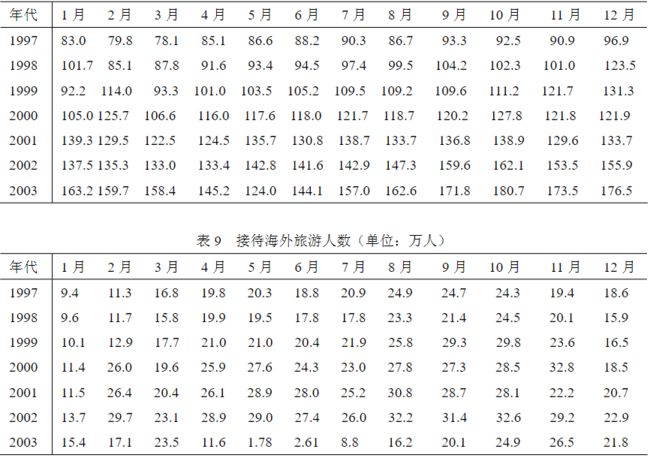
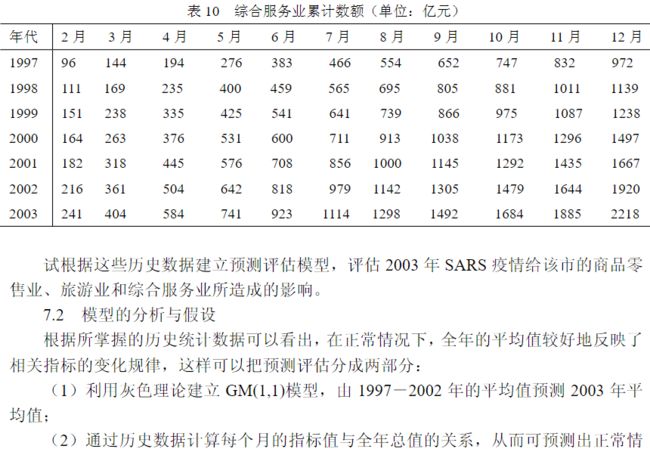
7.SARA疫情对某些经济指标影响问题

clc,clear
load han1.txt %把原始数据保存在纯文本文件han1.txt中
han1(end,:)=[];m=size(han1,2);
x0=mean(han1,2);
x1=cumsum(x0)
alpha=0.4;n=length(x0);
z1=alpha*x1(2:n)+(1-alpha)*x1(1:n-1)
Y=x0(2:n);B=[-z1,ones(n-1,1)];
ab=B\Y
k=6;
x7hat=(x0(1)-ab(2)/ab(1))*(exp(-ab(1)*k)-exp(-ab(1)*(k-1)))
z=m*x7hat
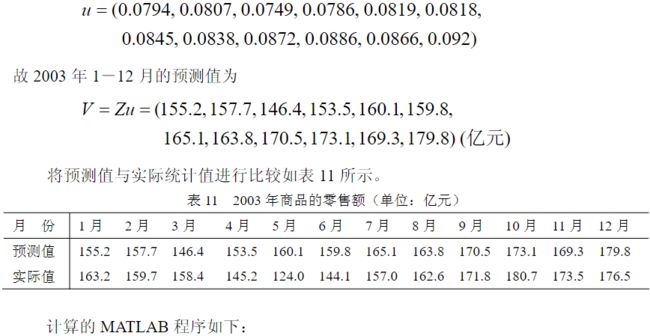
u=sum(han1)/sum(sum(han1))
v=z*u

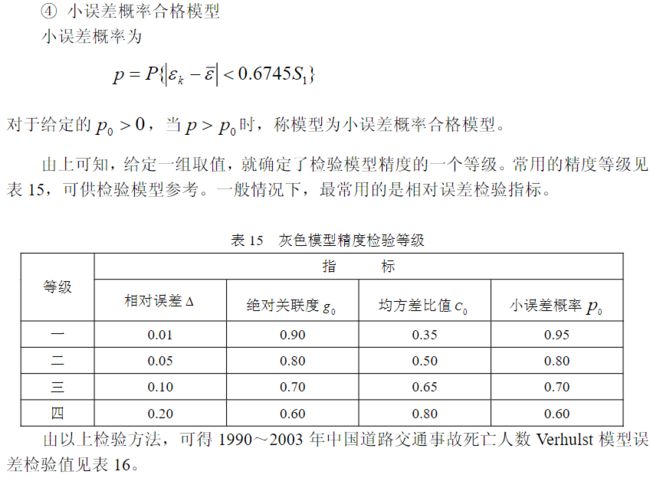
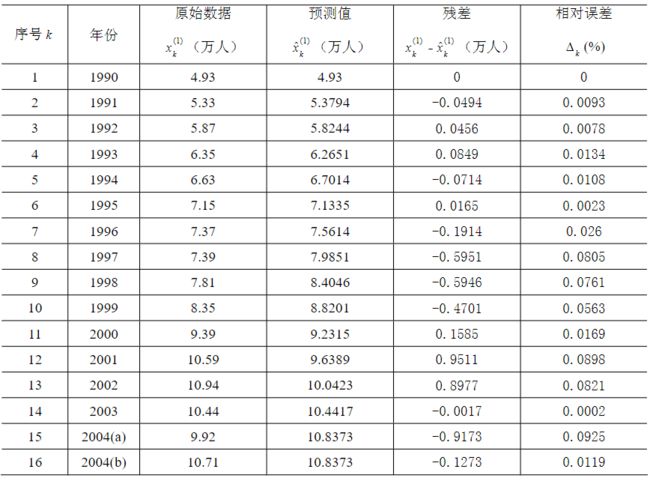
8.道路交通事故灰色Verhulst预测模型

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35
9.39 10.59 10.94 10.44];
n=length(x1);
nian=1990:2003;
plot(nian,x1,'o-');
x0=diff(x1);
x0=[x1(1),x0]
for i=2:n
z1(i)=0.5*(x1(i)+x1(i-1));
end
z1
B=[-z1(2:end)',z1(2:end)'.^2]
Y=x0(2:end)'
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b*x^2','x(0)=x0'); %求解常微分方程
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)}); %代入参数值
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测值
之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

clc,clear
x1=[4.93 5.33 5.87 6.35 6.63 7.15 7.37 7.39 7.81 8.35
9.39 10.59 10.94 10.44];
n=length(x1);
x0=diff(x1);
x0=[x1(1),x0]
for i=2:n
z1(i)=0.5*(x1(i)+x1(i-1));
end
B=[-z1(2:end)',ones(n-1,1)];
Y=x0(2:end)';
abhat=B\Y %估计参数 a,b 的值
x=dsolve('Dx+a*x=b','x(0)=x0');
x=subs(x,{'a','b','x0'},{abhat(1),abhat(2),x1(1)});
yuce=subs(x,'t',0:14) %计算预测值
digits(6); x=vpa(x) %显示微分方程的解，为了提高计算精度，把该语句放在计算预测
值之后，或者不使用该语句
yuce(16)=yuce(15);
x1_all=[x1,9.92,10.71];
epsilon=x1_all-yuce %计算残差
delta=abs(epsilon./x1_all) %计算相对误差
delta_mean=mean(delta) %计算平均相对误差
x1_all_0=x1_all-x1_all(1); %数据列的始点零化像
yuce_0=yuce-yuce(1); %数据列的始点零化像
s0=abs(sum(x1_all_0(1:end-1))+0.5*x1_all_0(end));
s1=abs(sum(yuce_0(1:end-1))+0.5*yuce_0(end));
tt=yuce_0-x1_all_0;
s1_s0=abs(sum(tt(1:end-1))+0.5*tt(end));
absdegree=(1+s0+s1)/(1+s0+s1+s1_s0) %计算灰色绝对关联度
c=std(epsilon,1)/std(x1_all,1) %计算标准差比值

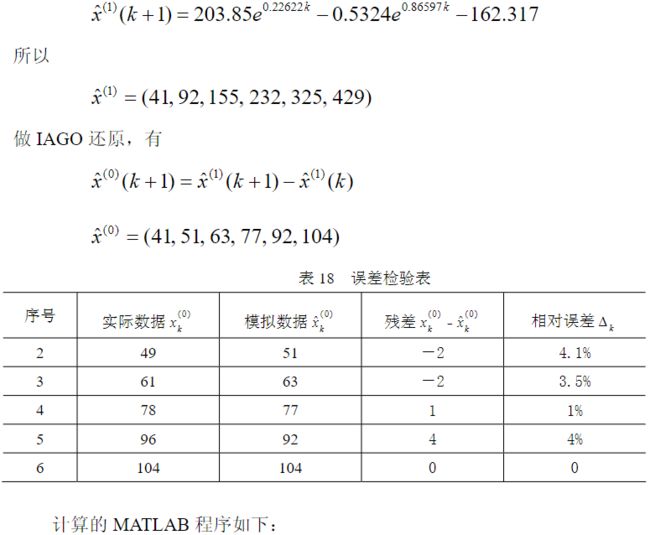
9.GM(2,1)和DGM模型

clc,clear
x0=[41,49,61,78,96,104];
n=length(x0);
x1=cumsum(x0)
a_x0=diff(x0);
a_x0=[0,a_x0]
for i=2:n
z(i)=0.5*(x1(i)+x1(i-1));
end
B=[-x0(2:end)',-z(2:end)',ones(n-1,1)];
Y=a_x0(2:end)';
u=B\Y
x=dsolve('D2x+a1*Dx+a2*x=b','x(0)=c1,x(5)=c2');
x=subs(x,{'a1','a2','b','c1','c2'},{u(1),u(2),u(3),x1(1),x1(6)});
yuce=subs(x,'t',0:n-1);
digits(6),x=vpa(x)
x0_hat=[yuce(1),diff(yuce)]
epsilon=x0-x0_hat
delta=abs(epsilon./x0)

clc,clear
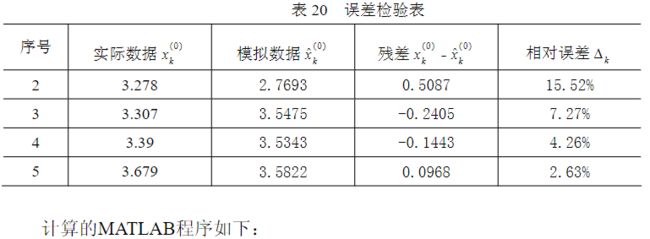
x0=[2.874,3.278,3.39,3.679,3.77,3.8];
n=length(x0);
a_x0=diff(x0);
a_x0=[0,a_x0]
B=[-x0(2:end)',ones(n-1,1)];
Y=a_x0(2:end)';
u=B\Y
x=dsolve('D2x+a*Dx=b','x(0)=c1,Dx(0)=c2');
x=subs(x,{'a','b','c1','c2'},{u(1),u(2),x0(1),x0(1)});
yuce=subs(x,'t',0:n-1);
digits(6),x=vpa(x)
x0_hat=[yuce(1),diff(yuce)]
epsilon=x0-x0_hat
delta=abs(epsilon./x0)

10.GM(1,N)和GM(0,N)模型

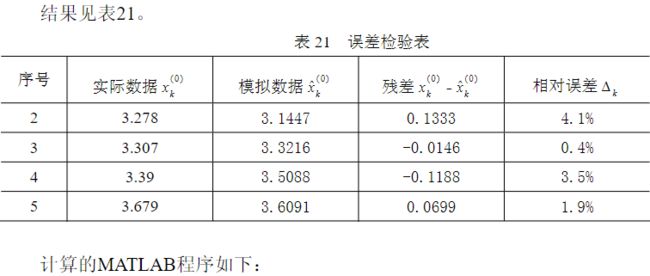
clc,clear
x10=[2.874,3.278,3.307,3.39,3.679];
x20=[7.04,7.645,8.075,8.53,8.774];
n=length(x10);
x11=cumsum(x10)
x21=cumsum(x20)
for i=2:n
z11(i)=0.5*(x11(i)+x11(i-1));
end
B=[-z11(2:n)',x21(2:n)'];
Y=x10(2:n)';
u=B\Y
x=dsolve('Dx+a*x=b*x2','x(0)=x0');
x=subs(x,{'a','b','x0','x2'},{u(1),u(2),x10(1),'x21'});
digits(6),x=vpa(x);x=simple(x)
x=subs(x,{'t','x21'},{[0:n-1],x21(1:n)})
xhat=[x(1),diff(x)]
epsilon=x10-xhat
delta=abs(epsilon./x10)

clc,clear
x10=[2.874,3.278,3.307,3.39,3.679];
x20=[7.04,7.645,8.075,8.53,8.774];
n=length(x10);
x11=cumsum(x10)
x21=cumsum(x20)
B=[ones(n,1),x21(1:n)'];
Y=x11(1:n)';
u=B\Y
x11hat=B*u
x10hat=[x11hat(1),diff(x11hat)']
epsilon=x10-x10hat
delta=abs(epsilon./x10)

11.总结