学习潘海东博士的《潮汐调和分析原理和应用》

        潘海东博士在B站（用户名：ocean_tide）分享了他的电子书《潮汐调和分析原理和应用》，以及他开发的潮汐调和分析工具包S_Tide，非常厉害。

       在学习《潮汐调和分析原理和应用》之前，我们需要安装matlab软件。

       1 、潮汐调和分析的本质：最小二乘拟合

       潮汐调和分析求解分潮振幅和迟角的过程本质就是最小二乘拟合。

       测绘专业的学生一般会学习自由网平差，解算误差方程就是用到最小二乘法，误差的平方和最小，求取观测值的最优估值。具体解算的过程是先输入观测值的初始值，求得误差值，计算误差的平方和，然后在用新的观测值（初始值+误差值）重新计算，求得新的误差值，然后计算误差的平方和，二次平方和相减，如果差值不满足要求，继续迭代，直至满足要求。

       测绘专业的学生要求用C语言实现这个过程。有了matlab，我们只需要会用就行。

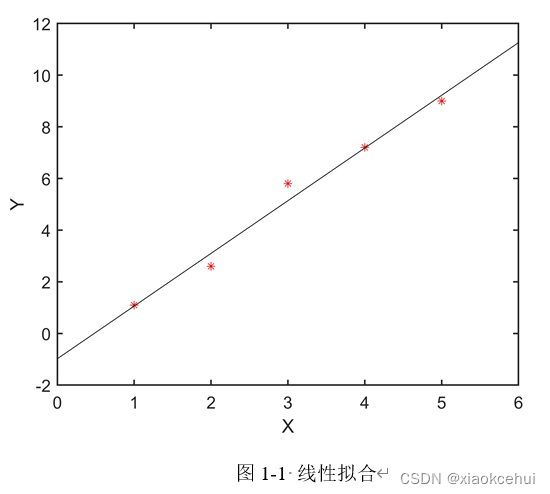
       图1-1展示了五个散点，通过最小二乘拟合，我们能基于这五个散点找到最优的直线（误差最小），即确定y=ax+b中的a和b。

绘制图1-1所用的MATLAB程序如下:

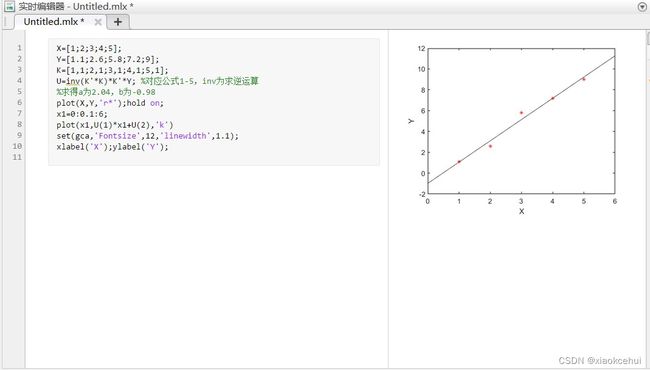
X=[1;2;3;4;5];

Y=[1.1;2.6;5.8;7.2;9];

K=[1,1;2,1;3,1;4,1;5,1];

U=inv(K'*K)*K'*Y; %对应公式1-5，inv为求逆运算

%求得a为2.04，b为-0.98

plot(X,Y,'r*');hold on;

x1=0:0.1:6;

plot(x1,U(1)*x1+U(2),'k')

set(gca,'Fontsize',12,'linewidth',1.1);

xlabel('X');ylabel('Y');

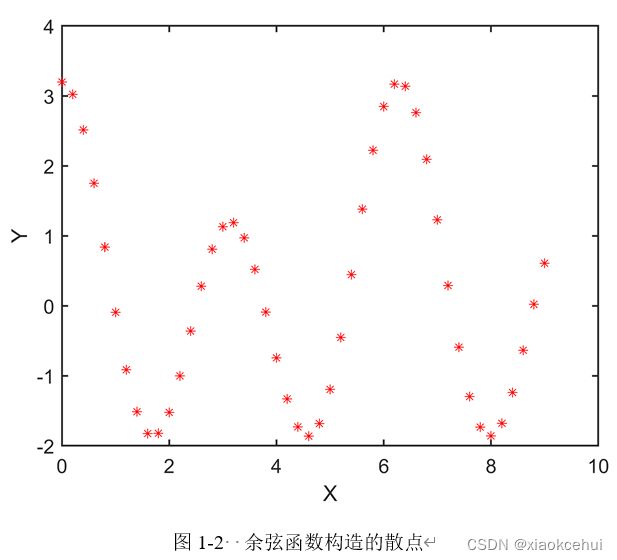
 曲线拟合，更加接近潮汐拟合。图1-2展示了一系列散点，这些散点由公式1-6构建，其中t=0:0.2:9, S=0.2, H1=1; H2=2。

                (1-6)

如何利用这些散点基于最小二乘法反推出平均水位S和振幅H1, H2。

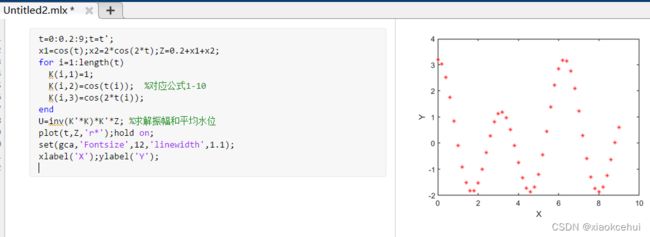
t=0:0.2:9;t=t';

x1=cos(t);x2=2*cos(2*t);Z=0.2+x1+x2;

for i=1:length(t)

  K(i,1)=1;

  K(i,2)=cos(t(i));  %对应公式1-10

  K(i,3)=cos(2*t(i));

end

U=inv(K'*K)*K'*Z; %求解振幅和平均水位

plot(t,Z,'r*');hold on;

set(gca,'Fontsize',12,'linewidth',1.1);

xlabel('X');ylabel('Y');

 

 在经典潮汐调和分析模型中（如公式1-11所示），水位被认为是一系列余弦函数线性叠加的结果，每一个余弦函数都代表了一个分潮：

 （详见下一节）。频率接近的分潮的集合称为潮族，主要潮族有半日潮族（即周期为0.5天左右），全日潮族（周期为1天左右）以及四分之一日潮族（周期为0.25天左右）。全日潮族代表性分潮为K1, 周期为23.93小时，半日潮族代表性分潮为M2，周期为12.42小时，四分之一日潮族代表性分潮为M4，周期为6.21小时。

使用矩阵运算编写潮汐调和分析程序不仅简单，而且还可以有效应对观测存在缺测或者采样不均匀等特殊情况。 如果观测水位里某个时刻存在缺测，只需要将公式1-15和1-16中该时刻对应的行删除即可。

mytide函数是笔者基于本节的矩阵算法编写的潮汐调和分析程序，短小精悍，不到30行即完成了调和分析。

 海水受到的引潮力是日地距离，日月距离，太阴赤纬，太阳赤纬等多个变量的非线性函数。

实际上，除了天文因素，河流径流、海冰、海洋层结等都会影响潮汐，而这些要素都存在显著的年循环，这导致M2分潮振幅存在显著的年循环，由积化和差可知会诞生两个新的分潮，标记为H1和H2分潮，因为这两个分潮不是天文要素产生的，所以不是天文分潮，一般称为气象分潮。

为什么太阴日是24.8412小时（24小时50分钟）？地球自转一圈需要24小时（转速15°/小时），月亮绕地球转一圈需要27.32天。太阴日是以月球为参考点所度量地球自转周期。月球公转方向和地球自转方向相同，地球自转一圈后，月亮公转了360°/27.32=13.2°，地球需要再转13.2/15小时（大约50分钟）。这也解释了为什么过了一天后，高潮会延后50分钟。

本节的模型没有考虑升交点的黄经的18.61年变化（即交点因子和交点订正角），所以无法做潮汐预报。

2、matlab使用问题

精度问题，尽量多使用矩阵运算，向量化编程，最大数组的维数，超大矩阵处理策略

T-Tide串联的矩阵的维度不一致的问题

3、潮汐调和分析和预报

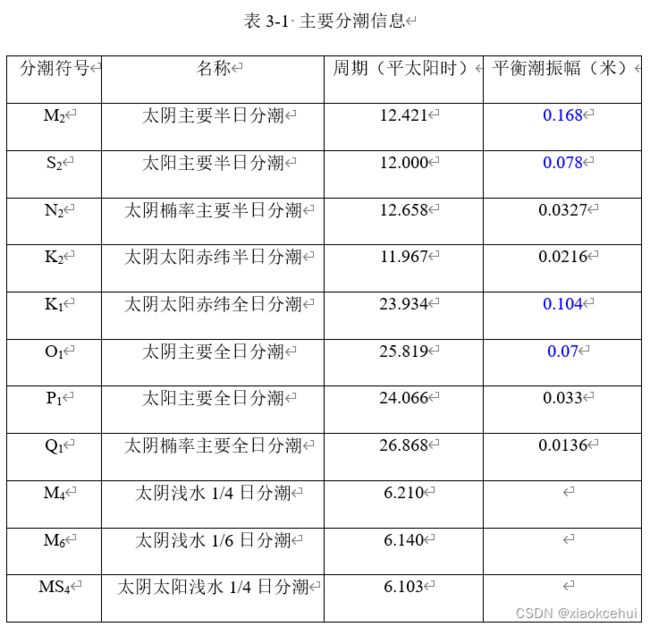
表3-1展示了8个平衡潮振幅最大的分潮（M2, S2, N2, K2, K1, O1, P1,Q1）和3个主要浅水分潮(M4, M6, MS4)。八大主要分潮中又以M2, K1, S2和O1这四个分潮平衡潮振幅最大，称为四大主要分潮。

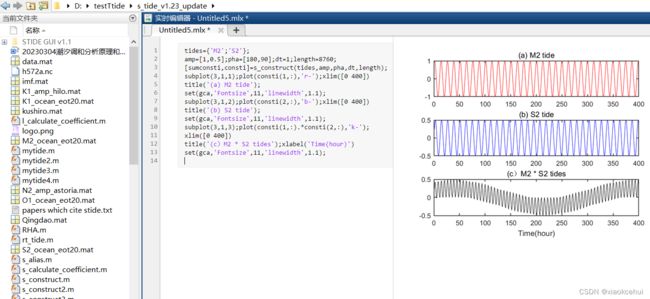
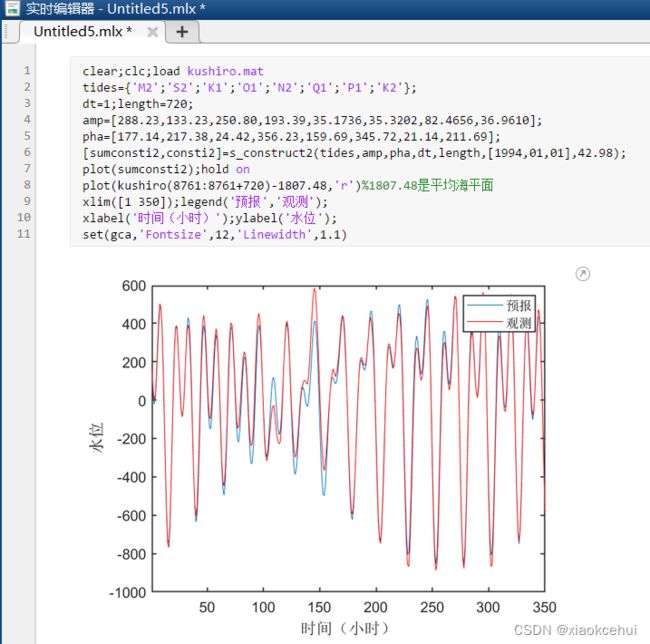
M2和S2分潮的非线性相互作用。构造潮位时使用了S_TIDE工具包里的s_construct函数。

 

 

 

在做潮汐调和分析时，已知水位观测的数据长度N，采样间隔t（单位一般是小时），可以分辨的分潮的频率差必须大于等于1/(Nt)。如果频率差小于1/(Nt)，则按照平衡潮振幅的大小来决定，振幅大的分潮保留，振幅小的舍弃。

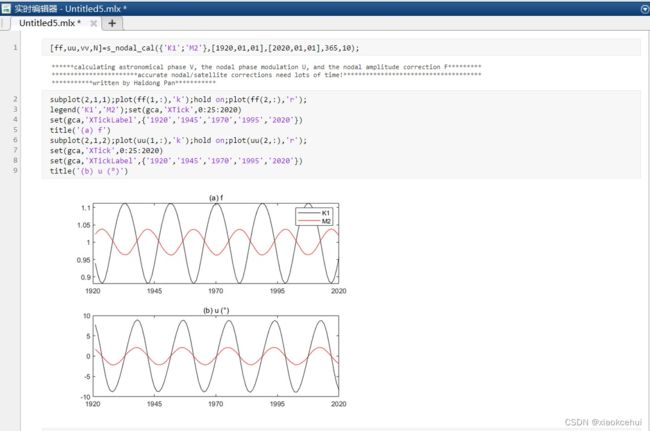
月球升交点的黄经N存在的18.61年循环（图3-3）会调制太阴分潮的振幅和迟角，通过积化和差产生一些小分潮，而将主要分潮和这些小分潮分开需要最少18.61年的数据，显然，很多验潮站的水位观测无法满足这个条件，故引入交点因子f和交点订正角u来消除18.61年的影响。

M2和K1分潮的交点因子f和交点订正角u随着时间的变化

 

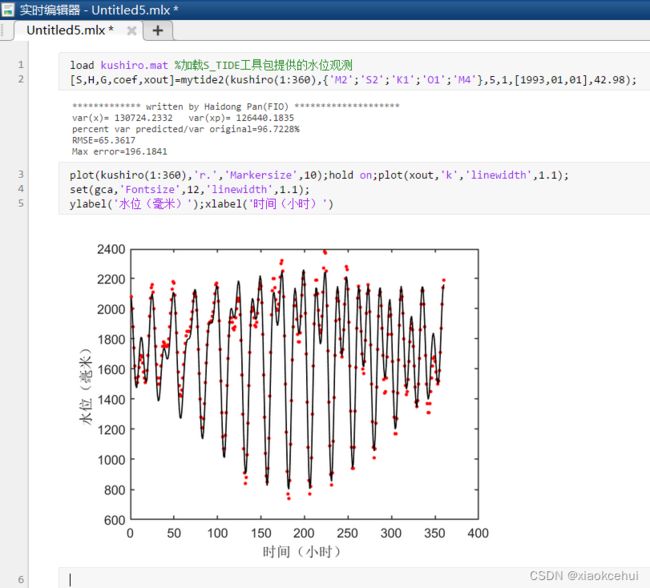
由于实际调和分析的潮位数据往往比较短（一年以内），而这么短的时间内交点因子和交点订正角的变化非常小，可以近似认为不变。故无须计算每时每刻的交点因子和交点订正角（这样很费时间），实际调和分析中往往只计算中间时刻的交点因子和订正角，然后作为分析时段的交点因子和订正角。T_TIDE工具包就采用了这个策略，因此其不适合分析长时间的潮位序列（显著大于1年）。下面的mytide2是在mytide函数基础上考虑中间时刻的交点因子、订正角和初相角修改而来的，其中stime代表待分析水位的起始时间，lat代表站点的纬度。该函数也添加到了S_TIDE工具包里。

考虑了交点因子和订正角后的回报结果（Kushiro)。红色点为实测，黑线为回报。

 通过潮汐调和分析得到了各个分潮的振幅和迟角后，再利用公式3-14，即可进行潮汐预报。如果预报的时间段在一年左右（或者更短），那么可以近似认为这段时间内交点因子和订正角都不变，进而加快计算，S_TIDE里的s_construct2函数即采用了这样的思路，显然这意味着该函数无法预报长期的潮位。S_TIDE里的s_consrtuct3函数弥补了这个不足，该函数计算每个时刻的交点因子和订正角，虽然准确，但是计算速度不快。

s_construct2的预报和Kushiro的观测对比

有了s_consturct2函数后，海洋工程和航海里常用的理论深度基准面的计算可以得到极大的简化。理论深度基准面即理论上可能最低潮面，目前通用算法是从八大主要分潮以及3个浅水分潮（M4, MS4和M6）的组合中找到最低水位。这个问题本质上就是求非线性函数极小值，这里的非线性函数指的是一系列正（余）弦函数的叠加，每个正（余）弦函数还存在18.61年循环。教材上对于理论深度基准面的求解过程非常复杂，编程实现也很麻烦。这里我们使用s_construct2函数基于11个主要分潮的调和常数重构长期的潮位，然后找到重构潮位的最小值，即理论深度基准面。S_TIDE工具包里的s_tdd函数就使用了这个方法，这个方法简单直接易懂，但是实现的前提是电脑计算能力的大幅度提高，在上个世纪60年代和70年代显然不具备这样的条件。s_estimate_max_tidalcurrent函数可以估算潮流的最大可能流速，原理与s_tdd函数类似。

 潮位和潮流的采样周期一般为1小时或者更高频。 但是卫星高度计观测的采样一般远远大于主要分潮周期。比如常用的T/P卫星，采样周期是9.9156天，这样会导致频率混淆，即半日和全日分潮的能量被混淆到了非常长的周期上。图3-9为频率混淆的示意图。读者可以使用S_TIDE里的s_alias函数计算指定分潮在指定采样频率下的混淆周期。M2分潮在9.9156天的采样周期下的混淆周期是62.11天，在35天的采样周期下的混淆周期是94.49天。依据公式3-3，在9.9156天采样周期下分辨八大主要分潮最少需要9.18年的数据。考虑到卫星高度计资料比较长，所以做调和分析时需要计算每个时刻的交点因子和订正角。

 

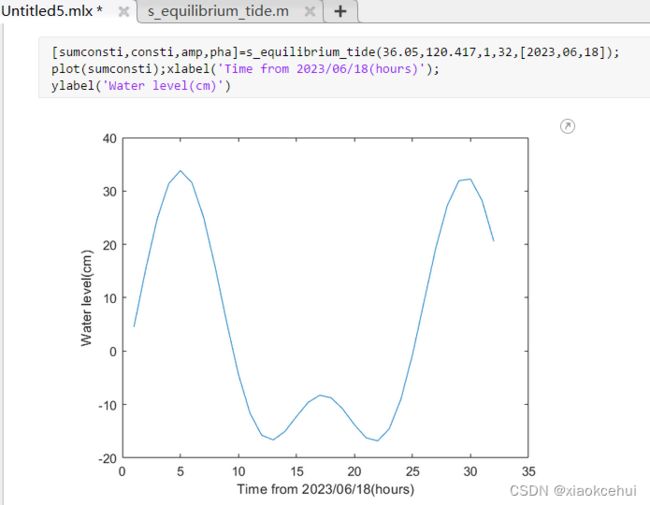
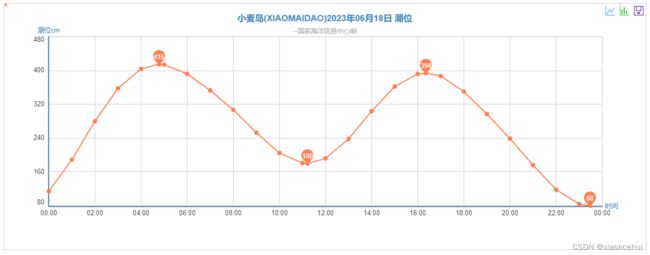
 s_equilibrium_tide函数计算的北纬36.05°，东经120.417°（小麦岛），自2023年6月18日零时起的逐时水位

上面是UTC时间，下面是北京时间，北京时间的0时是UTC+8，但是看两个曲线好像相关性不咋地啊。

平衡潮是个啥？

平衡潮理论假定：整个地球表面被等深海水所包围；海水没有惯性，也没有粘滞性，在重力与引潮力作用下，海水时时处于平衡状态。对于月球引潮力来说，月球垂直引潮力的方向与重力加速度方向相反；反之对于在通过地心、并与地月中心连线垂直的平面上的那些点，垂直引潮力与重力加速度方向一致。
因此，前者海面将稍稍升高，而后者海面将稍稍降低。通过这样的调整，海面重新形成一个等势面。这个新的等势面形状为一个椭球面，称为太阴“潮汐椭球”，如图1所示。由于地球的自转，在地壳上的一个固定点的海面便将发生周期性的涨落，从而形成潮汐。这就是平衡潮理论的基本思想。

参考文献 

潮汐调和分析原理与应用——20220310南京大学_哔哩哔哩_bilibili

S_TIDE相比T_TIDE优势 - 哔哩哔哩

致所有的S_TIDE使用者：你们的贡献不会被忽视 - 哔哩哔哩

chttps://www.cnblogs.com/jmliao/p/5575202.html

64位系统vs2010平台下实现C++与matlab R2014混合编程方法示例_add exported functions_Jerry-1990的博客-CSDN博客

C++ MATLAB 混合编程——VS项目调用MATLAB函数_c++调用matlab引擎_大作家佚名的博客-CSDN博客

Rich Pawlowicz's Matlab Stuff

MAT 文件版本- MATLAB & Simulink- MathWorks 中国

VS2017 MFC调用MATLAB2018b实现C++的混合编程_vs2017 调用matlab2018b_山川大海的博客-CSDN博客

MATLAB_R2018b安装教程_matlab2018b安装教程及激活_乘栩缘:VisualS的博客-CSDN博客

matlab2020a编译环境 MCR 安装步骤（非常实用）_matlab mcr_一米九零小胖子的博客-CSDN博客

C++调用matlab函数（未安装 matlab 也可以使用）_一米九零小胖子的博客-CSDN博客

mwArray和Mat之间的转化_mwarray转mat_一米九零小胖子的博客-CSDN博客