机器学习之k-means聚类二、啤酒聚类实现
文章目录
- 一、环境开发说明
- 二、基于前篇理论实现
-
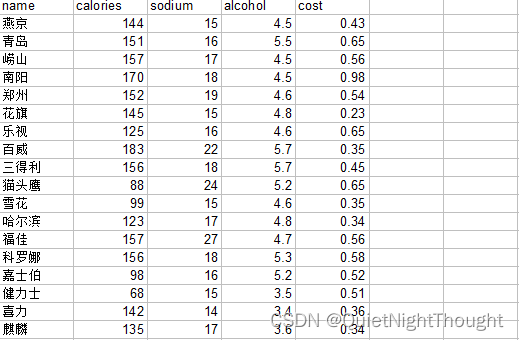
- 1. 数据说明
- 2. 具体实现流程
-
- a. 对数据进行标准化处理
- b. 使用手肘法进行K值得选择
- c. 算法实现,
- d.将聚类结果进行可视化
- e. 计算轮廓系数
- f. 轮廓系数可视化
- 三、 文中的完整代码
- 四、不调包实现
- 五、参考文献
一、环境开发说明
window环境
python 3.6.5
具体依赖包在项目文件中
二、基于前篇理论实现
聚类理论说明
代码敲起来,才能明白其中妙处
1. 数据说明
数据比较简单,没有过多的数据量,不过具备参考价值
2. 具体实现流程
我这里使用的是sklearn实现的流程,后面在手敲k-means聚类算法
这里的实现步骤,完全按照聚类算法原理中的算法实现步骤。
a. 对数据进行标准化处理
对数据的标准化处理比较简单,直接使用api来进行处理,只做演示,实际项目中会比这复杂的多:

b. 使用手肘法进行K值得选择
具体实现流程如下:计算原理看这里
def SSE():
#TODO 计算SSE进行k值得选择
clusters = 15
K = range(1,clusters+1)
TSSE = []
std = StandardScaler()
for k in K:
SSE = [] #用于存储各个簇内差平方法和
# 提取特征值 提取除了名字以外所有列信息
X = data.loc[:, ['calories', 'sodium', 'alcohol', 'cost']]
# print(X)
#todo 增加数据标准化
x = std.fit_transform(X)
#使用聚类 默认使用的是 init='k-means++' 进行初始化
#todo 首先,创建了一个KMeans对象kmean,并设置聚类中心的数量为3个。
kmean = KMeans(n_clusters=k, init='k-means++')
kmean.fit(x)
#todo 返回簇类标签
labels = kmean.labels_
print("labels:",labels)
#todo 返回簇类中心
centers = kmean.cluster_centers_
print("centers:", centers)
#todo 计算各个簇的差平方和,存入列表中
for label in set(labels):
res = np.sum((x[labels == label,]-centers[label,:])**2)
SSE.append(res)
TSSE.append(sum(SSE))
print(TSSE)
print(len(TSSE))
#todo 中文和负号的正常显示
plt.figure(figsize=(8, 6))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置绘图风格
plt.style.use('ggplot')
# 绘制K的个数与GSSE的关系
plt.plot(K, TSSE, 'b*-')
plt.xlabel('簇的个数')
plt.ylabel('簇内离差平方和之和')
# 显示图形
plt.show()
来看下展示的结果
 看到这里我们可以看到,并没有特别明显的拐点,但在簇为2的地方,相对来说还是比较明显的。
看到这里我们可以看到,并没有特别明显的拐点,但在簇为2的地方,相对来说还是比较明显的。
c. 算法实现,
def kemans():
# print(data)
# 提取特征值 提取除了名字以外所有列信息
X = data.loc[:, ['calories', 'sodium', 'alcohol', 'cost']]
# print(X)
#使用聚类 默认使用的是 init='k-means++' 进行初始化
#todo 首先,创建了一个KMeans对象kmean,并设置聚类中心的数量为3个。
kmean = KMeans(n_clusters=2, init='k-means++')
#todo 增加数据标准化
std = StandardScaler()
x = std.fit_transform(X)
#todo 然后,使用数据X对KMeans模型进行拟合(fit)操作,得到已经训练好的模型km。
km = kmean.fit(x)
#todo 将每个样本点所属的簇(cluster)标签(即聚类结果)添加到原始数据集data中,
# 并存储在一个名为"cluster"的新列中。这一步操作涉及到km.labels_属性,可以得到每个数据点分配给哪个簇。
data['cluster'] = km.labels_
# print(data)
'''
可以看到data中已经出现了簇的分类
km.labels_:是 KMeans 算法对每个样本点进行聚类后得到的簇标签。在 KMeans 模型中,每个簇都有一个编号(从0开始)
name calories sodium alcohol cost cluster
0 燕京 144 15 4.5 0.43 1
1 青岛 151 16 5.5 0.65 2
2 崂山 157 17 4.5 0.56 2
3 南阳 170 18 4.5 0.98 2
4 郑州 152 19 4.6 0.54 2
5 花旗 145 15 4.8 0.23 1
6 乐视 125 16 4.6 0.65 0
'''
#todo 最后:使用groupby方法按照"cluster"列进行分组,并计算每个簇的均值,从而得到聚类中心。
# 这些聚类中心被存储在centers变量中。
# centers = data.groupby('cluster').mean().rest_index()
centers = data.groupby('cluster').mean()
# print(centers)
'''
来看下结果的打印情况
calories sodium alcohol cost
cluster
0 88.250000 17.500000 4.625000 0.507500
1 160.250000 19.375000 5.062500 0.583750
2 135.666667 15.666667 4.283333 0.391667
一般来说,X应该是一个二维数组,其中每行表示一个数据样本,每列表示一个特征。
K-means算法会针对这些特征对所有数据点进行聚类,最终返回每个数据点所属的簇(cluster)标签,
并生成相应的聚类中心。
'''
return centers
d.将聚类结果进行可视化
e. 计算轮廓系数
使用api进行直接计算
#todo 然后,使用数据X对KMeans模型进行拟合(fit)操作,得到已经训练好的模型km。
km = kmean.fit(x)
#todo 将每个样本点所属的簇(cluster)标签(即聚类结果)添加到原始数据集data中,
# 并存储在一个名为"cluster"的新列中。这一步操作涉及到km.labels_属性,可以得到每个数据点分配给哪个簇。
data['cluster'] = km.labels_
# print(data)
'''
km.labels_:是 KMeans 算法对每个样本点进行聚类后得到的簇标签。在 KMeans 模型中,每个簇都有一个编号(从0开始)
name calories sodium alcohol cost cluster
0 燕京 144 15 4.5 0.43 1
1 青岛 151 16 5.5 0.65 2
2 崂山 157 17 4.5 0.56 2
3 南阳 170 18 4.5 0.98 2
4 郑州 152 19 4.6 0.54 2
5 花旗 145 15 4.8 0.23 1
6 乐视 125 16 4.6 0.65 0
'''
#todo 进行轮廓系数进行评估
sil = silhouette_score(x,data.cluster)
来看下计算结果:
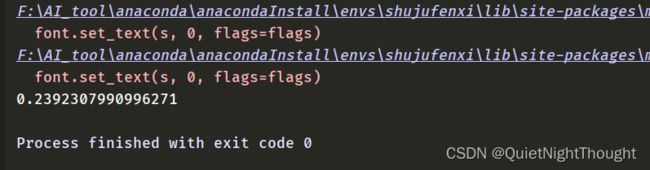 可以看到0.23这个数字还是很小的因此,这个聚类效果不是很理想。
可以看到0.23这个数字还是很小的因此,这个聚类效果不是很理想。
f. 轮廓系数可视化
我们看下,在不同簇的情况下,轮廓系数的变化:
结果如下:
_score = []
for i in range(2,16):
labels = KMeans(n_clusters=i, init='k-means++').fit(x).labels_
scores = silhouette_score(x,labels)
_score.append(scores)
plt.plot(list(range(2,16)),_score)
plt.xlabel("簇类中心数目")
plt.ylabel("轮廓系数")
plt.show()
结果展示:

可以看到,随着簇的数量增加,轮廓系数处于下降趋势
三、 文中的完整代码
调包实现完整代码
四、不调包实现
不调包实现源码
五、参考文献
[1]https://www.jianshu.com/p/b268d7f3fbb9
[2]https://zhuanlan.zhihu.com/p/432230028