基于BG/NBD概率模型的用户CLV预测

基于BG/NBD概率模型的用户CLV预测

小P：小H，我们最近想预测下用户的生命周期价值，有没有什么好的方法啊？

小H：简单啊，$CLV=用户每月平均花费\ast 用户平均寿命$。用户每月平均花费根据历史数据就能算出来；用户平均寿命可以根据流失率简单计算下$用户平均寿命=1/平均每月用户流失率$，或者也可以用生存分析预测下用户平均寿命。

小P：额，你懂的模型那么多，就不能直接利用算法预测每个用户的CLV吗？

小H：这…，那好吧，有个BG/NBD概率模型可以依据用户的RFM进行预测

如果你想知道用户是不是流失了呢？还有多少付费潜力呢？在未来某段时间是否会再次购买呢？BG/NBD概率模型都可以解决。但是该模型不能预测周期性消费的客户，因为它只关注T时段内的交易。

该模型的假设前提比较强，但在日常消费中一般都符合，所以可以放心使用

• 交易假设1：用户在活跃状态下，一个用户在时间段t内完成的交易数量服从均值为λt的泊松分布
• 交易假设2：用户的交易率λ服从形状参数为r，逆尺度参数为α的gamma分布
• 流失假设1：每个用户在交易j完成后流失的概率服从参数为p(流失率)的几何分布
• 流失假设2：用户的流失率p服从形状参数为a，b的beta分布
• 联合假设：每个用户的交易率λ和流失率p互相独立
• 混合分布理解：指数分布与Gamma分布的混合分布为Pareto分布；而泊松分布与Gamma分布的混合分布为负二项分布

数据探索

# pip install lifetimes

import pandas as pd
import numpy as np
import warnings
import matplotlib.pyplot as plt
import seaborn as sns
import lifetimes
import toad 
from lifetimes.utils import *
from lifetimes import BetaGeoFitter
from lifetimes import GammaGammaFitter
from lifetimes.plotting import *

# 初始化设置
%matplotlib inline
pd.set_option('display.max_columns', None) # 显示所有列
sns.set(style="ticks")

以下数据如果有需要的同学可关注公众号HsuHeinrich，回复【数据挖掘-CLV预测】自动获取～

# 读取数据
raw_data = pd.read_excel('Online Retail.xlsx')
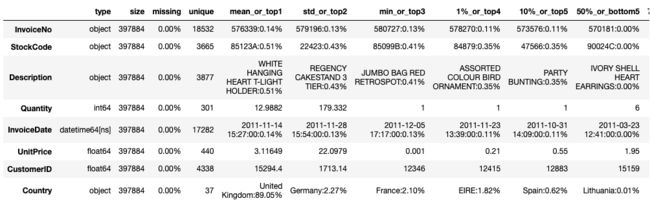
raw_data.head()

主要字段含义：InvoiceNo:订单ID、StockCode:产品ID、Quantity:数量、UnitPrice:单价、CustomerID:客户ID

# 查看数据信息
toad.detector.detect(raw_data)

# 数据处理
df=raw_data.copy()
# 剔除缺失的CustomerID
df.dropna(subset=['CustomerID'],inplace=True)
# 剔除Quantity<=0 or UnitPrice<=0的数据
df.query('Quantity > 0 & UnitPrice >0', inplace=True)
# 生成结果数据
raw_result = df.copy()
# 再次查看数据信息
toad.detector.detect(raw_result)

特征工程

模型的主要输入参数为RF:T，因此需要构建出该输入数据

• R：recency=客户最后一次购买商品和第一次购买商品的时间差
• F：frequency=客户重复购买商品的期间数（模型中会减去1表示复购，即0表示1次购买，0次复购）
• T=数据集中的最后一天与客户第一次购买商品的时间差

# 函数方式-通过lifetimes的summary_data_from_transaction_data
df_model=raw_result.copy()
# 生成价格数据
df_model['Sales']=df_model['Quantity']*df_model['UnitPrice']
# 生成观察日期
last_date=df_model.InvoiceDate.max()
df_temp = summary_data_from_transaction_data(df_model, 'CustomerID', 'InvoiceDate',
                         monetary_value_col='Sales',
                         observation_period_end=last_date)
df_temp.sort_values('monetary_value', ascending=True).head()

	frequency	recency	T	monetary_value
CustomerID
12346.0	0.0	0.0	325.0	0.0
15130.0	0.0	0.0	169.0	0.0
15127.0	0.0	0.0	65.0	0.0
17852.0	0.0	0.0	11.0	0.0
15120.0	0.0	0.0	133.0	0.0

# 构造模型数据
df_model_finall=df_temp.copy()

当然也可以自己手动计算RF:T

# 构造模型输入数据RF:T
df_model=raw_result.copy()
# 生成价格数据
df_model['Sales']=df_model['Quantity']*df_model['UnitPrice']
# 生成观察日期
last_date=df_model.InvoiceDate.max()
# 手动计算
df_model.set_index('CustomerID',inplace=True)
df_temp2=df_model.groupby('CustomerID').agg(
 # 计算RF：T
 max_date=('InvoiceDate','max'),
 min_date=('InvoiceDate','min'),
 frequency=('InvoiceDate',lambda x: pd.Series(x.dt.to_period('D')).nunique()), # 按日计算频次
 recency=('InvoiceDate',lambda x: (max(x.dt.to_period('D')) - 
                                   min(x.dt.to_period('D')))/np.timedelta64(1, 'D')), # 按日计算最近时间差
 T=('InvoiceDate',lambda x: (pd.Timestamp(last_date).to_period('D')-
                             min(pd.Series(x.dt.to_period('D'))))/np.timedelta64(1,'D')), # 按日计算观察时间差
 Invoice_count=('InvoiceNo','nunique'), # 计算订单数
 Stock_count=('StockCode','count'), # 计算产品数
 Sales_sum=('Sales','sum'), # 计算销售额总额
)
df_temp2['Sales_mean']=df_temp2['Sales_sum']/df_temp2['frequency']
df_temp2.sort_values('Sales_mean', ascending=True).head()

对比与life包的函数计算的结果，我们发线存在一些差异，这是因为函数只计算复购的情况。具体如下（其中复购日期为不包含首次购买日期）

	frequency	recency	Sales_mean	T
人工计算	购买日期按日去重	末次与首次购买日期差（D）	销售总额/frequency	观察日与首次购买日期差（D）
函数计算	复购日期按日去重	末次与首次购买日期差（D）	复购总额/frequency	观察日与首次购买日期差（D）

lifetimes的summary_data_from_transaction_data函数也可以通过参数设置是否包含首次购买，还可以自定义计算周期

# summary_data_from_transaction_data可以通过参数设置日期差的方式，是否包含首次购买
df_model=df.copy()
# 生成价格数据
df_model['Sales']=df_model['Quantity']*df_model['UnitPrice']
# 生成观察日期
last_date=df_model.InvoiceDate.max()
df_temp3 = summary_data_from_transaction_data(df_model, 'CustomerID', 'InvoiceDate',
                      monetary_value_col='Sales',
                      observation_period_end=last_date,
                      freq='W',
                      include_first_transaction='True'
                      )
df_temp3.sort_values('frequency', ascending=True).head()

	frequency	recency	T	monetary_value
CustomerID
12346.0	1.0	0.0	46.0	77183.60
15243.0	1.0	0.0	10.0	316.68
16400.0	1.0	0.0	13.0	303.93
13927.0	1.0	0.0	10.0	348.99
13926.0	1.0	0.0	3.0	223.85

模型拟合

# 模型拟合
bgf = BetaGeoFitter(penalizer_coef=0)
bgf.fit(df_model_finall['frequency'], df_model_finall['recency'], df_model_finall['T'])

结果展示

用户预期交易热力图

# 用户预期交易热力图
fig = plt.figure(figsize=(12,8))
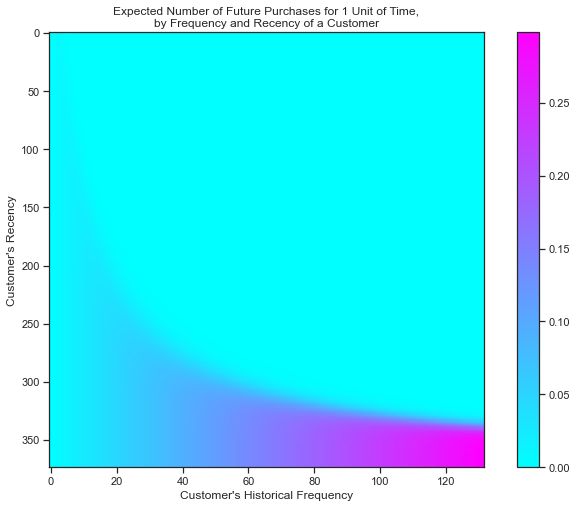
plot_frequency_recency_matrix(bgf, T=1, cmap='cool')
plt.show()

• 潜在客户：右下角红色区域用户，这部分用户购买频次高，且距离上购买较久。因此在未来T=1（默认）期间预期购买数最多
• 冷客户：右上角冷色区域用户，这部分用户在最近快速购买，因此在未来T=1（默认）期间预期购买数最少
• 不确定客户（长尾客户）：暖蓝色区域（20，250）附近，这部分客户不经常来，最近也没见过，因此不确定是否还会购买

用户留存概率热力图

# 用户留存概率热力图
fig = plt.figure(figsize=(12,8))
plot_probability_alive_matrix(bgf, cmap='cool')
plt.show()

• 暖红色为大概率存活的用户
• 冷蓝色为大概率流失的用户

预测下个时期的购买量

# 预测用户下个时期（t）的预期购买量
t = 30
df_model_finall['predicted_purchases'] = bgf.conditional_expected_number_of_purchases_up_to_time(t, 
                                  df_model_finall['frequency'], df_model_finall['recency'], df_model_finall['T'])
df_model_finall.sort_values(by='predicted_purchases', ascending=False).head()

	frequency	recency	T	monetary_value	predicted_purchases
CustomerID
14911.0	131.0	372.0	373.0	1093.661679	8.948135
12748.0	112.0	373.0	373.0	301.024821	7.658492
17841.0	111.0	372.0	373.0	364.452162	7.590548
15311.0	89.0	373.0	373.0	677.729438	6.097251
14606.0	88.0	372.0	373.0	135.890114	6.029322

例如客户14911历史购买了131次，且最近一次购买在372天。在未来30天预期有8.9天的购买。

gamma-gamma模型估算客户终生价值

# 我们仅估算至少有一次重复购买的客户
df_gg_model=df_model_finall[df_model_finall['frequency']>0]
df_gg_model.shape

(2790, 5)

# 前提假设：购买频次和购买金额无相关性
df_gg_model[['monetary_value', 'frequency']].corr()

	monetary_value	frequency
monetary_value	1.000000	0.015906
frequency	0.015906	1.000000

# 模型拟合
ggf = GammaGammaFitter(penalizer_coef = 0)
ggf.fit(df_gg_model['frequency'],
        df_gg_model['monetary_value'])

# 预测每笔交易的预期收益
ggf.conditional_expected_average_profit(
        df_gg_model['frequency'],
        df_gg_model['monetary_value'])

CustomerID
12347.0    569.978836
12348.0    333.784235
12352.0    376.175359
12356.0    324.039419
12358.0    539.907126
              ...    
18272.0    474.368524
18273.0    201.838133
18282.0    260.340479
18283.0    174.532812
18287.0    492.169257
Length: 2790, dtype: float64

# 预测用户未来的CLV
bgf.fit(df_gg_model['frequency'], df_gg_model['recency'], df_gg_model['T'])
ggf.customer_lifetime_value(
    bgf, # bgf预测用户未来的预期购买量
    df_gg_model['frequency'],
    df_gg_model['recency'],
    df_gg_model['T'],
    df_gg_model['monetary_value'],
    time=12, # 用户的预期寿命，以月为单位
    freq='D', # T的单位,默认为'D'
    discount_rate=0.01 # monthly discount rate ~ 12.7% annually
)

CustomerID
12347.0    3194.349694
12348.0    1175.905597
12352.0    2472.058198
12356.0     979.177238
12358.0    1940.851493
              ...     
18272.0    3111.075131
18273.0     723.867524
18282.0    1026.433547
18283.0    1966.557687
18287.0    2070.391699
Name: clv, Length: 2790, dtype: float64

模型评估

# 预期购买次数校验
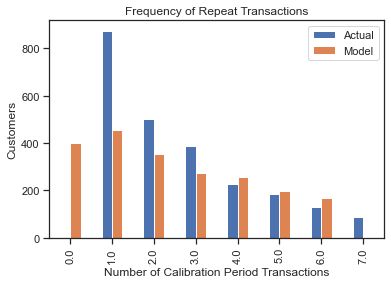
plot_period_transactions(bgf)
plt.show()

预测与实际值接近，模型似乎不错

# 分数据集校准

# 设置校准结束时间，观察结束时间，对数据集划分
summary_cal_holdout = calibration_and_holdout_data(raw_result, 'CustomerID', 'InvoiceDate',
                                        calibration_period_end='2011-05-01',
                                        observation_period_end='2011-12-9' )  
# 拟合查看校准结果
bgf = BetaGeoFitter(penalizer_coef=0.1)
bgf.fit(summary_cal_holdout['frequency_cal'], summary_cal_holdout['recency_cal'], 
        summary_cal_holdout['T_cal'])
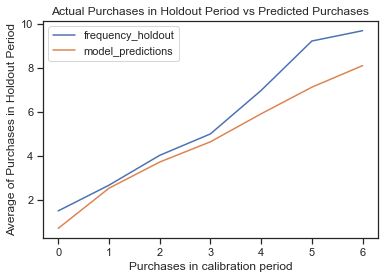
plot_calibration_purchases_vs_holdout_purchases(bgf, summary_cal_holdout)
plt.show()

/Users/heinrich/opt/anaconda3/lib/python3.8/site-packages/pandas/core/series.py:726: RuntimeWarning: invalid value encountered in sqrt
  result = getattr(ufunc, method)(*inputs, **kwargs)
/Users/heinrich/opt/anaconda3/lib/python3.8/site-packages/pandas/core/series.py:726: RuntimeWarning: invalid value encountered in log
  result = getattr(ufunc, method)(*inputs, **kwargs)

• penalizer_coef=0时不收敛，更改为0.1。
• 模型预测的效果在0-4次较为接近，在5、6购买预测存在低估情况

总结

这个模型实际只依赖RFT进行训练和预测，虽然大多数消费数据的概率分布服从假设，但是在使用时应该结合业务数据进行预测效果验证，毕竟和钱相关的任务都是很重要的，不可含糊～

共勉～

参考

• 用户增长 - BG/NBD概率模型预测用户生命周期LTV
• 如何计算用户生命周期价值（CLV）
• 使用lifetimes进行客户终身价值（CLV）探索
• 官方案例演示
• lifetimes官方文档