用零知识证明桥接多链宇宙

1. 引言

bridge为双向通讯协议，用于向目标链C2上某应用 证明 在源链C1上发生了某事件，或 用于向目标链C1上某应用 证明 在源链C2上发生了某事件。链之间传输信息可为：

• messages
• funds
• 或 其它数据

源链C1上的state change可在目标链C2上进行链上验证，通常是以合约形式实现对方链的light client：C2上的合约持续跟踪C1链的区块头，以Merkle proof来验证源链提交的root。
通常C1、C2采用不同的field和曲线，验证操作需要out of field arithmetic。此外，随着区块头的持续增加，client需要存储并验证新的区块头，这将导致大量的计算和存储开销，且通常效率低下。为了绕过该问题，很多bridge采用了更集中的方式来构建：

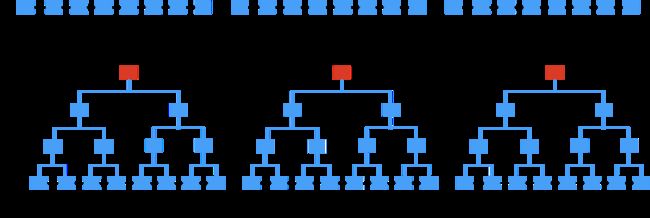
上图这样的light client protocol构建存在致命的缺陷：一小组trusted validators来对state changes进行签名。其信任假设为信任中心化的bridging entity，通常为一小撮trusted parties，这与区块链的基础原则相违背，会带来censorship和security问题。

尽管桥很有用，但搭建风险也很大。区块链历史上一些最昂贵的Hack仅针对桥。根据Vulnerabilities in Cross-chain Bridge Protocols Emerge as Top Security Risk，过去一年来，69%的资金丢失源于对bridge的攻击，损失达数十亿美金：

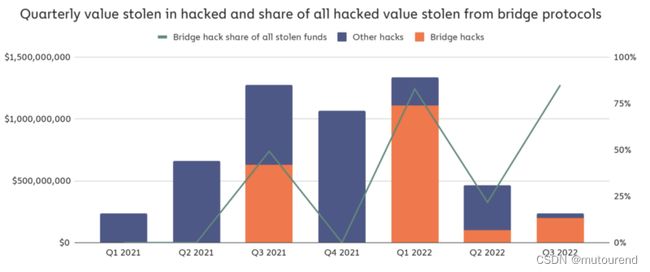
根据 BlueHat IL 2022 - Niv Yehezkel - A primer on cross-chain bridges and how to break one 可知，这样的安全弱点的根本原因在于bridge充当了中心化的存储单元。大多数现有bridge（for liquidity）采用Lock-Mint-Burn-Release机制。经典的逻辑为：用户发送资金到C1链上的bridge合约以“lock”资金，即这些资金在C1中不再可用；然后bridge允许用户在C2链上mint出等量的资金；用户使用了部分资金之后，想要将剩余资金退回到C1链，可“burn” C2链上资金，一旦bridging entity验证通过后，可在C1链上“release”剩余的资金。这样的链间bridge，会有大量的资金待着bridge中，而其安全性仅依赖于少量的trusted parties，使其成为主动攻击的目标。

构建bridge的主要技术难点在于：

• 1）低计算开销（高效处理跨链数据、高效处理out of field arithmetic）
• 2）低存储开销（Succinctness）
• 3）安全性/trustless（Soundness）

本文重点关注基于零知识证明（Zero Knowledge Proofs，ZKP）所构建实现的桥，主要对比了：

• Succinct Labs的Bridge方案：Succinct Verification of Proof of Consensus
• Electron Labs的Bridge方案：Bringing IBC to Ethereum
• Berkley RDI的Bridge方案：zkbridge
  

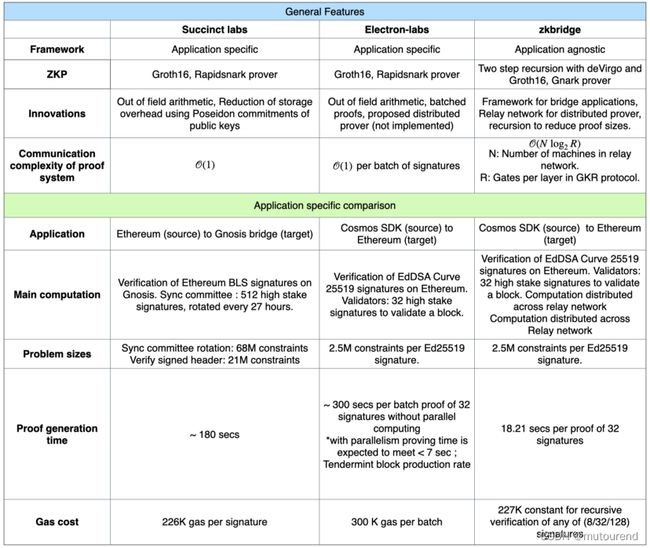
总之，使用ZKP设计的bridge解决了去中心化和安全性问题，但由于large circuit size，其引入了计算瓶颈问题。计算开销问题可通过以下手段改进：

• 硬件加速
• 使用特定的SNARKs
• 一些技巧，如对public data进行commit，以减少存储开销。

由于bridge work的大部分工作是proving data-parallel circuit，使用类似deVirgo这样的可并行化ZKP方案是一个值得研究的方案。

此外，多链宇宙中的链采用了不同的field和curve，从最底层来说，对field arithmetic进行优化是关键基石。通过MPC来实现proof generation的并行化，将引入MPC本身存在的communication complexity瓶颈问题，这也是一个未决问题。

2. Bridge & ZKP

近年来，ZKP在rollups中的应用有了长足进展，ZKP的soundness属性支持安全、去中心化应用。这也意味着，ZKP可探索用于构建bridge，目前在该领域主要有3大有趣的开发方向：

• 1）Succinct Labs 2022年9月发表 Towards the endgame of blockchain interoperability with proof of consensus：其方案为Succinct verification of consensus with zkSNARKs，其使用a single zk-SNARK实现了以太坊PoS（Proof of Stake）light client。详细可见Zero Knowledge Summit Berlin 2022 (Full Live Stream)中分享。
• 2）Electron Labs https://github.com/Electron-Labs：其方案为bringing IBC（Inter Blockchain Communication）to Ethereum with zkSNARKs，目前已有一个工作原型，借助a single zk-SNARK将Cosmos SDK（Tendermint）bridge 到以太坊light client。
• 3）Berkley RDI zkBridge: Trustless Cross-chain Bridges Made Practical：基于Tiancheng Xie等人2022年论文zkBridge: Trustless Cross-chain Bridges Made Practical。使用a 2 step recursive zk-SNARK，实现了将Cosmos SDK bridge到以太坊轻节点，以及将以太坊轻节点 bridge到 EVM兼容链（本文不覆盖该内容）。

以上项目借助zk-SNARKs的属性，重新定义了bridge的设计思想。以上所有方案，都假定了，存在某轻节点协议，使得节点可同步固化的区块链状态对应的区块头。

借鉴ZKP rollup技术 到 ZKP bridge，主要存在2大挑战：

• 1）bridge中涉及的circuit size要比rollup大数个数量级；
• 2）如何降低链上的存储和计算开销。

3. Succinct Labs的Bridge方案：Succinct Verification of Proof of Consensus

Succinct Labs的Bridge方案为：Succinct Verification of Proof of Consensus，利用了zk-SNARK的succinct属性（而不是Zero Knowledge属性），来在链上验证consensus validity proofs。目前已在Gnosis链与以太坊链之间构建了a trust minimized bridge，具体见：

• ZK Beacon Chain Light Client Spec (Gnosis Chain version)：Gnosis Chain是eth2的canary链。Gnosis希望为beacon链共识（在Gnosis链上）实现一个基于ZK的轻节点客户端，它可以由链外用户或（bridge中的）EVM合约验证。由于信标链使用BLS12-381，目前没有Eth预编译程序，使用ZK有助于克服高昂的gas开销。实现基于ZK的轻节点，需要为sync committee生成SNARK证明。这包含了512个validators，约每27小时（256个epoch）轮换一次，因此，对延迟的需求是最低的。（尽管若轻节点更新越频繁，意味着在该27小时期间需要处理更多的区块头和签名。）

以太坊每27小时需随机选出512个validators组成sync committee。这些被选中的validators需在该27小时期间为每个区块头签名，若某区块头获得超过2/3 validators的签名，则认为其状态为有效状态。验证过程包含了：

• 1）验证区块头的Merkle proof；
• 2）验证在sync committee的validators的Merkle proof；
• 3）验证BLS signatures for correct rotation of the sync committee。

以上验证要求每27小时在链上存储512个BLS公钥，验证每个区块头时需验证其签名，从而在链上会有基于BLS12-381曲线的512次Elliptic curve additions 和 1次pairing check，相应的开销是高昂难以承受的。Succinct Labs Bridge方案的核心思想为：

• 使用zk-SNARK（Groth16）来生成（constant size的）validity proof，该证明可在Gnosis链上高效验证。

以太坊轻节点使用Gnosis链上的某solidity合约，而链下计算包含：

• 1）构建验证validators及其BLS签名的circom circuits
• 2）计算zk-SNARK proof

然后，区块头和相应的proof会提交到该智能合约，该合约会在Gnosis链上验证相应的区块头及其proof。
SNARK部分的circuit size和proving time总结为：

优化点包括：

• 使用ZK friendly Poseidon hash 对512个validator的公钥进行commit。为此，使用Poseidon哈希可解决存储开销的问题，并降低circuit size。降低circuit size的原因在于：
  • 每27小时会更新trusted committee，且之前的committee使用SSZ（Simple Serialization）的SHA256序列对new committee进行数字签名。不同于直接将其用于SNARK中——将创建large circuits（每个bitwise操作对应一个gate，而SHA运算中有大量bitwise操作），而是对当前公钥使用Poseidon hash进行commit——对应为a SNARK friendly representation of the corresponding circuit。

Succinct Labs的Bridge方案的特点在于：

• 所使用的桥接方案与特定应用强相关（依赖于共识协议），并从zk-SNARKs的soundness属性中派生其安全性。
• 此外，借助优化，可实现低存储开销、降低circuit复杂度，实现succinct verification并可generalizable。但是使用zk-SNARK会降低所追求的信任假设。

4. Electron Labs的Bridge方案：Bringing IBC to Ethereum

Electron Labs致力于使用IBC（Inter-Blockchain Communication）构建从Cosmos SDK生态 到 所有自治链的 bridge。
不过，不同于Succinct Labs的Bridge方案，Electron Labs的Bridge方案需在以太坊合约内验证某（Cosmos SDK）轻节点。实际上，在以太坊上运行其它链的轻节点看起来是充满挑战的。
在Cosmos SDK中，其Tendermint轻节点是运行在twisted Edwards curve（Ed25519）之上的，而以太坊链上并不原生支持Ed25519曲线。因此，在以太坊（BN254）链上验证Ed25519签名的效率不高且开销巨大。

Cosmos SDK的每个区块头都包含了约128个EdDSAq签名（基于Ed25519曲线），这些签名由一组validators签署（验证一个区块需要有32个high stake签名）。验证这些签名将生成large circuits——这将是相当大的计算组件。基本问题就在于，如何在以太坊链上高效验证来自其它链的ed25519签名。解决方案为，在链下生成signature validity proof，然后在以太坊链上仅验证该proof本身。
circom库支持BN128/BLS12-381/Ed448-Goldilocks曲线，而ed25519的base field为$p=2^{255}-19$，为支持ed25519曲线的模运算，需将ed25519的单个field element以3个85 bit整数来表示，详细见：

• 使用Circom，来定义Ed25519 maths in R1CS model

circom生成的为Ed25519 signature verification circuit的R1CS表示，包含了上面定义的Elliptic curve point additions/doublings模运算。具体见：

• https://github.com/Electron-Labs/ed25519-circom

借助circom构建的Ed25519 signature verification circuit对应为 每个验签约200万个约束。

witness computation之后，借助https://github.com/iden3/rapidsnark Rapidsnark库来为ed25519 signature verification生成Groth16 proof。由于ed25519 curve signatures不支持aggregation，因此，无法像BLS签名那样为aggregated signatures生成a single SNARK proof。不过，ed25519签名支持verified in batches，其proof-time与batch内的签名数量呈线性关系。

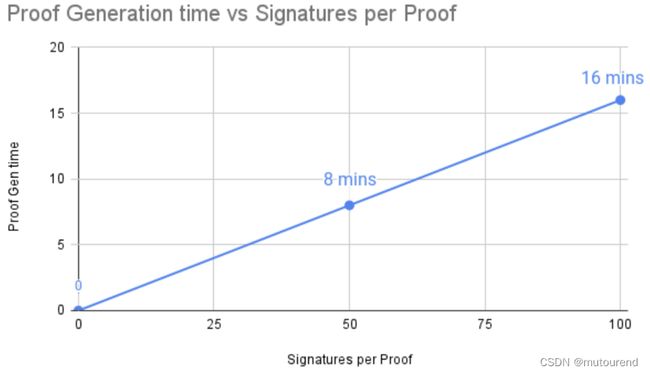
因此，若减少batch内的签名数量，可降低proof time（降低延迟），但由于会增加为每个batch生成的proof数量，会增加开销（gas费）。

Electron Labs Bridge方案的特点在于：

• 所使用的桥接方案与特定应用强相关（依赖于共识协议），并从zk-SNARKs的soundness属性中派生其安全性。
• 需在以太坊上验证Tendermint轻节点的ed25519签名，无需引入任何新的信任假设。
• 使用Circom，来定义Ed25519 maths in R1CS model 这种out of field modular arithmetic方案，是链上计算验证的一种很有价值的优化。
• Cosmos SDK的产块间隔约为7秒，为了跟上产块速率，prover time应大大降低。Electron Labs提出了使用多台机器并行计算来生成proof，以保证生成证明的速度与产块速度一致，且借助recursion 来生成a single zk-SNARK proof，详细见：
  • Bringing IBC to Ethereum using ZK-Snarks

5. Berkley RDI的Bridge方案：zkbridge

不同于以上2种industry-led ZKP bridge方案，zkbridge可基于多个应用来构建。其思想与前2种方案类似，在2条链上需要一个轻节点和合约来跟踪对应对方链的最新状态的digest。bridge的核心组件为：

• 1）block header relay network
• 2）updater contract
• 3）应用相关的合约（sender：SC1，receiver：SC2）

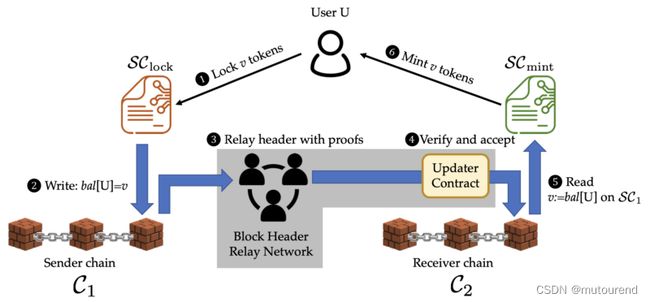
block header relay network由一组relay nodes组成，这些relay nodes会监听所桥接链的状态改变，并从全节点中获取相应的block headers。

bridge中relay node的主要功能为：

• 生成ZKP proof，以证明源链上区块头的正确性，同时，将该区块头及相应的证明 relay到目标链的updater contract。updater contract会验证该证明，若验证通过则接受该区块头，否则拒绝。与上面industry-led方案最大的不同点在于，zkbridge的信任假设减少为了：只要relay network中存在一个诚实的节点，则zk-SNARK是sound的。

Berkley RDI Bridge方案zkbridge的关键创新在于：

• 并行使用Virgo prover zkSNARK算法，具有succinct verification/proof size且不需要trusted setup，详细见论文：

  • Virgo prover是指论文 Virgo: Zero Knowledge Proofs System without Trusted Setup
  • deVirgo是指论文 zkBridge: Trustless Cross-chain Bridges Made Practical

  动机在于：验证N个签名的circuit 本质上是包含了 N份完全相同的sub-circuits，名为data-parallel circuit，每个sub-circuit是相互排斥的。适于上面的ed25519验签场景。

Virgo prover是基于GKR protocol的zero knowledge扩展，其为layered circuit中的每个sub-circuit运行sum check arguments 和 a polynomial commitment scheme。deVirgo在一组relay nodes上运行a Virgo prover，避免the linear growth of the proof size by aggregating the proofs and polynomial commitments into a master node。以ed25519签名为例，相应的circuit size为：

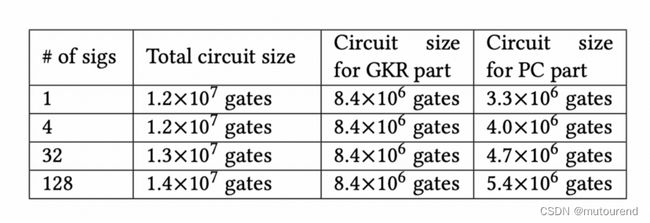
对于验证100个签名的circuit，其有约1千万个gates，proof size为210KB（与Virgo prover相同）。zkbridge采用2-step recursion：

• 1）第一步，生成a deVirgo proof。
• 2）使用Groth16 prover对deVirgo proof进行压缩。Groth16 verifier会生成 a proof of integrity of the execution of the deVirgo circuit。

采用recursion的各奔目的是为了实现：

• 1）succinctness（proof size）
• 2）减少验证gas开销

relay network会将Groth16 proof提交到updater contract进行链上验证。

deVirgo proof system为抗量子攻击的，因其仅依赖抗碰撞哈希函数，主要的计算瓶颈在于大size的circuit中的Number Theoretic Transforms（NTT）。
同时，zkbridge的relay network计算将存在与MPC一样的communication complexity问题，这同样会影响prover time。
GKR multilayered sum-check protocol的communication complexity为O(N log_2(gates per layer))，其中N为relay network中的机器数。以32个签名，32台机器为例，relay network中的communication轮数将相对较大，从而可能抵消分布式计算所带来的性能提升。

zkbridge包含一个relay network，负责fetch Cosmos区块头，并为分布式proof generation生成一个deVirgo proof。
然后，https://github.com/ConsenSys/gnark 的改编版（使用Electron-labs的https://github.com/Electron-Labs/ed25519-circom 中的优化signature verification circuit），用于以上第二步的recursion Groth16 proof生成。

以太坊端的updater contract以Solidity实现，持续跟踪Cosmos区块头以及relay network的Groth16 proof。由于Groth16 proof为constant size，相应的链上验证开销为<230K gas的常量值。未来，可能可批量验证B各连续的区块头，并为这B个区块头生成一个proof。但是，随着batch size的增加，prover time也将增加，不过由于减少了链上的验证压力，gas开销将随之减少。硬件加速可进一步改进Gnark prover。

zkBridge的特点在于：

• 其是在bridge纸上构建应用的框架；
• 使用一个relay network来生成zkp，从而在本文所有方案中，具有最小的信任假设。
• 只要可克服relay network中类似MPC的communication complexity，可使用任意可并行化的ZK prover。
• 除deVirgo relay network的MPC complexity之外，relay node的单个Virgo prover组件的瓶颈在于NTT。

6. 为何说多链宇宙是碎片化的？

根据An overview of the layer 1 blockchain ecosystem 可知，目前有多于100个Layer 1区块链协议，这些链具有其自身的共识机制、设计、应用、用户场景。

根据V神2021年博客 Why sharding is great: demystifying the technical properties 可知：

区块链协议存在不可能三角问题：

• 1）去中心化
• 2）安全性
• 3）可扩展性

多链宇宙中的跨链通信，通常称为互操作层，作为不同链之间的bridge基础设施。bridge会是碎片化的多链宇宙 去碎片化，目前有很多跨链bridge项目，详细可参看：

• Cross-chain solutions public
  
  

参考资料

[1] Ingonyama团队2022年10月博客 Bridging the Multichain Universe with Zero Knowledge Proofs