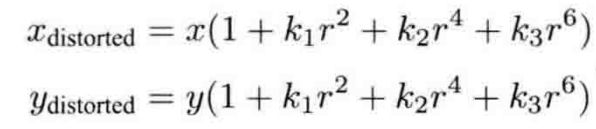相机坐标系

• 物距：被拍摄物体到凸透镜的距离
• 像距：成像平面到凸透镜的距离
• 焦距：凸透镜中心到焦点的距离

四个坐标系分别为：世界坐标系，相机坐标系，图像坐标系，像素坐标系

• 世界坐标系（world coordinate），也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置
• 相机坐标系{camera}：坐标原点为相机的光心位置，X 轴和Y 轴分别平行于图像坐标系的X轴和 Y 轴，Z轴为相机的光轴
• 图像坐标系：像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样
• 像素坐标系：就是看到相机拍出来保存下来的图像。一般情况下相机坐标系光轴都在相机中心，所以成像的图像坐标系原点也在中心，然后人为转换到左上角原点的像素坐标系上

像素坐标系到图像坐标系

u-v坐标系表示看到相机保存下来的照片，x-y坐标系是成像的位置坐标系，可以认为是传感器实际成像区域，从图中位置可以看出x-y坐标系原点在u-v坐标系（u0,v0）上，因此可得变换关系：


$dx，dy$为相机的固有参数，针对某一个型号传感器来说是固定的，分别表示在x，y方向上每个像素位置占多少毫米（mm/pixel），即$1pixel=dxmm$，$u_0，v_0$一般指图像上的中心位置，可能有一点点偏差。转换成齐次坐标形式就是

图像坐标系到相机坐标系

根据针孔相机原理，相机坐标系上物体在图像坐标系上成立倒像，依据三角形相似可以得出

转换为矩阵形式：

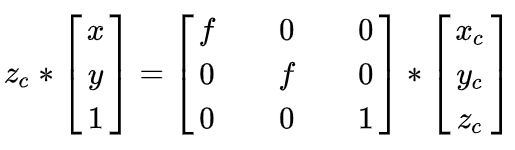
其中Zc是相机坐标系某点所在的深度值。

其中$f$为焦距，$f=|o-o_c|，f_x=f/dx，f_y=f/dy$，中间矩阵称为相机的内参，一般认为是相机的固定参数。

世界坐标系和相机坐标系的转换

外部世界是一个大坐标系，相机在这个坐标系上一个点，相机前面有另外一个点，这个点假设在相机坐标系上的坐标是$（x_c,y_c,z_c）$，在世界坐标系上的坐标是$（x_w,y_w,z_w）$，想想一下上下左右前后的移动相机，就可以移动到这个点在两个坐标系中坐标一样，称为刚性变换。

公式右侧矩阵分别记为旋转矩阵$R$，平移矩阵$T$，成为相机的外参。用于多个传感器之间的标定。

添加畸变

径向畸变：

切向畸变：

对于相机坐标系中的一点P，可以通过5个畸变系数找到这个点在像素平面上的正确位置：

python代码，从雷达到像素

# lidar -- camera -- pixel
param['rotate_vec'] = np.mat([1.5131235448660183, -1.504080508615343, 1.0724538041051752])
param['trans_vec'] = np.mat([-219.992648, 164.662458, 222.462379])
param['in_param'] = np.mat([[1152.85, 0, 957.033], [0, 1147.63, 529.578], [0, 0, 1.0]])
param['dist_vec'] = np.mat([-0.3272, 0.0985, 0.000015, 0.00049, 0])

camera_res = (np.dot(rot_mat, (np.array(p) * 10).reshape(-1, 1)) + np.array(param["trans_vec"]).T).squeeze()
# add distort
camera_res = camera_res / camera_res[2]
r = math.sqrt(camera_res[0] ** 2 + camera_res[1] ** 2)
tem_cam_x = camera_res[0] * (1 + k1 * math.pow(r, 2) + k2 * math.pow(r, 4) + k3 * math.pow(r, 6))
tem_cam_y = camera_res[1] * (1 + k1 * math.pow(r, 2) + k2 * math.pow(r, 4) + k3 * math.pow(r, 6))
tem_cam_x = tem_cam_x + 2 * p1 * camera_res[0] * camera_res[1] + p2 * (r ** 2 + 2 * camera_res[0] ** 2)
tem_cam_y = tem_cam_y + p1 * (r ** 2 + 2 * camera_res[1] ** 2) + 2 * p2 * camera_res[0] * camera_res[1]
camera_res[0] = tem_cam_x
camera_res[1] = tem_cam_y
img_x, img_y, _ = np.dot(np.array(param['in_param']), camera_res)

参考资料：
3x4 Projection Matrix