《斯坦福数据挖掘教程·第三版》读书笔记（英文版）Chapter 8 Advertising on the Web

来源：《斯坦福数据挖掘教程·第三版》对应的公开英文书和PPT

Chapter 8 Advertising on the Web

There are several factors that must be considered in evaluating ads:

1. The position of the ad in a list has great influence on whether or not it is clicked. The first on the list has by far the highest probability, and the probability drops off exponentially as the position increases.
2. The ad may have attractiveness that depends on the query terms. For example, an ad for a used convertible would be more attractive if the search query includes the term “convertible,” even though it might be a valid response to queries that look for that make of car, without specifying whether or not a convertible is wanted.
3. All ads deserve the opportunity to be shown until their click probability can be approximated closely. If we start all ads out with a click probability of 0, we shall never show them and thus never learn whether or not they are attractive ads.

There will be some constant c less than 1, such that on any input, the result of a particular on-line algorithm is at least c times the result of the optimum off-line algorithm. The constant c, if it exists, is called the competitive ratio for the on-line algorithm.

A matching is a subset of the edges such that no node is an end of two or more edges. A matching is said to be perfect if every node appears in the matching. Note that a matching can only be perfect if the left and right sets are of the same size. A matching that is as large as any other matching for the graph in question is said to be maximal.

Suppose $M_o$ is a maximal matching, and $M_g$ is the matching that the greedy algorithm produces. Let L be the set of left nodes that are matched in $M_o$ but not in $M_g$. Let R be the set of right nodes that are connected by edges to any node in L. We claim that every node in R is matched in $M_g$. Suppose not; in particular, suppose node r in R is not matched in $M_g$. Then the greedy algorithm will eventually consider some edge $(\ell ,r)$, where $\ell$ is in L. At that time, neither end of this edge is matched, because we have supposed that neither $\ell$ nor r is ever matched by the greedy algorithm. That observation contradicts the definition of how the greedy algorithm works; that is, the greedy algorithm would indeed match $(\ell ,r)$. We conclude that every node in R is matched in $M_g$.
Now, we know several things about the sizes of sets and matchings.

1. $|M_o|\le |M_g|+|L|$, since among the nodes on the left, only nodes in L can be matched in $M_o$ but not $M_g$.
2. $|L|\le |R|$, because in $M_o$, all the nodes in L were matched.
3. $|R|\le |M_g|$, because every node in R is matched in $M_g$.

Definition of the Adwords Problem

Given:

1. A set of bids by advertisers for search queries.
2. A click-through rate for each advertiser-query pair.
3. A budget for each advertiser. We shall assume budgets are for a month, although any unit of time could be used.
4. A limit on the number of ads to be displayed with each search query.

Respond to each search query with a set of advertisers such that:

1. The size of the set is no larger than the limit on the number of ads per query.
2. Each advertiser has bid on the search query.
3. Each advertiser has enough budget left to pay for the ad if it is clicked upon.

The revenue of a selection of ads is the total value of the ads selected, where the value of an ad is the product of the bid and the click-through rate for the ad and query. The merit of an on-line algorithm is the total revenue obtained over a month (the time unit over which budgets are assumed to apply). We shall try to measure the competitive ratio for algorithms, that is, the minimum total revenue for that algorithm, on any sequence of search queries, divided by the revenue of the optimum off-line algorithm for the same sequence of search queries.

There is a simple improvement to the greedy algorithm that gives a competitive ratio of 3/4 for the simple case of Section 8.4.3. This algorithm, called the Balance Algorithm, assigns a query to the advertiser who bids on the query and has the largest remaining budget. Ties may be broken arbitrarily.

When there are many advertisers, the competitive ratio for the Balance Algorithm can be under 3/4, but not too far below that fraction. The worst case for Balance is as follows.

1. There are N advertisers, $A_1,A_2,...,A_N$ .
2. Each advertiser has a budget $B=N!$.
3. There are N queries $q_1,q_2,...,q_N$ .
4. Advertiser $A_i$ bids on queries $q_1,q_2,...,q_i$ and no other queries.
5. The query sequence consists of N rounds. The ith round consists of B occurrences of query $q_i$ and nothing else.

The competitive ratio is $1-\frac{1}{e}$ , or approximately 0.63.

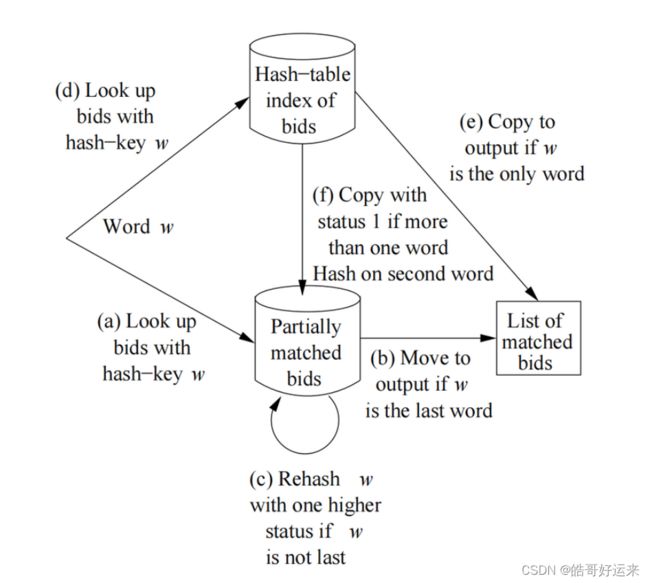
There are two new elements in the representation.

First, we shall include a status with each list of words. The status is an integer indicating how many of the first words on the list have been matched by the current document. When a bid is stored in the index, its status is always 0.

Second, while the order of words could be lexicographic, we can lower the amount of work by ordering words rarest-first. However, since the number of different words that can appear in emails is essentially unlimited, it is not feasible to order all words in this manner. As a compromise, we might identify the n most common words on the Web or in a sample of the stream of documents we are processing. Here, n might be a hundred thousand or a million. These n words are sorted by frequency, and they occupy the end of the list, with the most frequent words at the very end. All words not among the n most frequent can be assumed equally infrequent and ordered lexicographically. Then, the words of any document can be ordered. If a word does not appear on the list of n frequent words, place it at the front of the order, lexicographically. Those words in the document that do appear on the list of most frequent words appear after the infrequent words, in the reverse order of frequency (i.e., with the most frequent words of the documents ordered last).

The bids are stored in a hash-table, whose hash key is the first word of the bid, in the order explained above. The record for the bid will also include information about what to do when the bid is matched. The status is 0 and need not be stored explicitly. There is another hash table, whose job is to contain copies of those bids that have been partially matched. These bids have a status that is at least 1, but less than the number of words in the set. If the status is i, then the hash-key for this hash table is the **(i + 1)**st word. The arrangement of hash tables is suggested by Fig. 8.5. To process a document, do the following.

1. Sort the words of the document in the order discussed above. Eliminate duplicate words.

2. For each word w, in the sorted order:
   (i) Using w as the hash-key for the table of partially matched bids, find those bids having w as key.
   (ii) For each such bid b, if w is the last word of b, move b to the table of matched bids.
   (iii) If w is not the last word of b, add 1 to b’s status, and rehash b using the word whose position is one more than the new status, as the hash-key.
   (iv) Using w as the hash key for the table of all bids, find those bids for which w is their first word in the sorted order.
   (v) For each such bid b, if there is only one word on its list, copy it to the table of matched bids.

   (vi) If b consists of more than one word, add it, with status 1, to the table of partially matched bids, using the second word of b as the hash-key.

3. Produce the list of matched bids as the output.

The benefit of the rarest-first order should now be visible. A bid is only copied to the second hash table if its rarest word appears in the document. In comparison, if lexicographic order was used, more bids would be copied to the second hash table. By minimizing the size of that table, we not only reduce the amount of work in steps 2(i)–2(iii), but we make it more likely that this entire table can be kept in main memory.

Summary of Chapter 8

• Targeted Advertising: The big advantage that Web-based advertising has over advertising in conventional media such as newspapers is that Web advertising can be selected according to the interests of each individual user. This advantage has enabled many Web services to be supported entirely by advertising revenue.
• On- and Off-Line Algorithms: Conventional algorithms that are allowed to see all their data before producing an answer are called off-line. An on-line algorithm is required to make a response to each element in a stream immediately, with knowledge of only the past, not the future elements in the stream.
• Greedy Algorithms: Many on-line algorithms are greedy, in the sense that they select their action at every step by minimizing some objective function.
• Competitive Ratio: We can measure the quality of an on-line algorithm by minimizing, over all possible inputs, the value of the result of the online algorithm compared with the value of the result of the best possible off-line algorithm.
• Bipartite Matching: This problem involves two sets of nodes and a set of edges between members of the two sets. The goal is to find a maximal matching – as large a set of edges as possible that includes no node more than once.
• On-Line Solution to the Matching Problem: One greedy algorithm for finding a match in a bipartite graph (or any graph, for that matter) is to order the edges in some way, and for each edge in turn, add it to the match if neither of its ends are yet part of an edge previously selected for the match. This algorithm can be proved to have a competitive ratio of 1/2; that is, it never fails to match at least half as many nodes as the best off-line algorithm matches.
• Search Ad Management: A search engine receives bids from advertisers on certain search queries. Some ads are displayed with each search query, and the search engine is paid the amount of the bid only if the queryer clicks on the ad. Each advertiser can give a budget, the total amount they are willing to pay for clicks in a month.
• The Adwords Problem: The data for the adwords problem is a set of bids by advertisers on certain search queries, together with a total budget for each advertiser and information about the historical click-through rate for each ad for each query. Another part of the data is the stream of search queries received by the search engine. The objective is to select on-line a fixed-size set of ads in response to each query that will maximize the revenue to the search engine.
• Simplified Adwords Problem: To see some of the nuances of ad selection, we considered a simplified version in which all bids are either 0 or 1, only one ad is shown with each query, and all advertisers have the same budget. Under this model the obvious greedy algorithm of giving the ad placement to anyone who has bid on the query and has budget remaining can be shown to have a competitive ratio of 1/2.
• The Balance Algorithm: This algorithm improves on the simple greedy algorithm. A query’s ad is given to the advertiser who has bid on the query and has the largest remaining budget. Ties can be broken arbitrarily.
• Competitive Ratio of the Balance Algorithm: For the simplified adwords model, the competitive ratio of the Balance Algorithm is 3/4 for the case of two advertisers and $1-\frac{1}{e}$, or about 63% for any number of advertisers.
• The Balance Algorithm for the Generalized Adwords Problem: When bidders can make differing bids, have different budgets, and have different click-through rates for different queries, the Balance Algorithm awards an ad to the advertiser with the highest value of the function $\Psi =x(1-e^{-f}).$ Here, x is the product of the bid and the click-through rate for that advertiser and query, and f is the fraction of the advertiser’s budget that remains unspent.
• Implementing an Adwords Algorithm: The simplest version of the implementation serves in situations where the bids are on exactly the set of words in the search query. We can represent a query by the list of its words, in sorted order. Bids are stored in a hash table or similar structure, with a hash key equal to the sorted list of words. A search query can then be matched against bids by a straightforward lookup in the table.
• Matching Word Sets Against Documents: A harder version of the adwords-implementation problem allows bids, which are still small sets of words as in a search query, to be matched against larger documents, such as emails or tweets. A bid set matches the document if all the words appear in the document, in any order and not necessarily adjacent.
• Hash Storage of Word Sets: A useful data structure stores the words of each bid set in the order rarest-first. Documents have their words sorted in the same order. Word sets are stored in a hash table with the first word, in the rarest-first order, as the key.
• Processing Documents for Bid Matches: We process the words of the document rarest-first. Word sets whose first word is the current word are copied to a temporary hash table, with the second word as the key. Sets already in the temporary hash table are examined to see if the word that is their key matches the current word, and, if so, they are rehashed using their next word. Sets whose last word is matched are copied to the output.

END