【知识点随笔分享 | 第一篇】避不开的浮点误差

  引入：

各位在大一初入C语言的时候，老师肯定说过浮点数之间的比较要用做差法，当二者的差值特别小甚至于接近0的时候，这两个数就相等，不知道各位是否会有疑惑？为什么浮点数不可以直接进行比较呢？

#include
int main()
{
	double a = 0.1;
	double b = 0.2;
	

	if ((a + b) == 0.3)
	{
		printf("true");
	}
	else
	{
		printf("false");
	}
}

这段代码非常简单，就是判断用浮点数存储的0.1+0.2是否等于0.3。

运行结果竟然是不等于。但是实际知识告诉我们0.1+0.2确实等于0.3，那么为什么比较不相等呢？
我们单独查看一下 浮点数0.1+0.2的值：
我们发现：原来浮点数0.1+0.2并不完全等于0.3，怎么尾部还有这么多数字？
其实这就是我们今天要介绍的内容：浮点误差

浮点误差：

想要探寻误差的起源，我们就要介绍一下IEEE-754是什么东西，它详细的规定了浮点数字在计算机中的二进制存储规则。
 

IEEE-754是一种国际通用的二进制浮点数标准，它规定了浮点数在计算机系统内部的表达方式和相应的计算规则，目的是为了提高不同计算机系统之间浮点数的互操作性和可移植性。

IEEE-754标准定义了两种浮点数格式，分别是单精度浮点数和双精度浮点数。其中，单精度浮点数包含32位，双精度浮点数包含64位。这两种格式都被广泛使用，尤其是在科学计算和工程领域中。

IEEE-754标准还规定了浮点数的符号位、指数位和尾数位的分布，以及浮点数的四种运算方式（加、减、乘、除）和异常处理方式。其中，浮点数的指数采用移码表示，可以表示正数、负数和零，浮点数的精度和有效数字也会随着指数的变化而变化。

在实际应用中，IEEE-754标准的浮点数格式和计算规则被广泛应用于各种编程语言和计算机系统中，如C语言、Java、Python等，也为高性能计算和大规模科学计算提供了重要的技术支持。

EEE-754标准规定了两种浮点数格式，分别是单精度浮点数和双精度浮点数，具体如下：

1. 单精度浮点数：32位二进制，有1位符号位、8位指数位和23位尾数位。最高位为符号位，0表示正数，1表示负数。接下来的8位指数位采用移码表示，可以表示正数、负数和零。23位尾数位包括整数部分和小数部分，用于保存有效数字和精度。

2. 双精度浮点数：64位二进制，有1位符号位、11位指数位和52位尾数位。最高位为符号位，0表示正数，1表示负数。接下来的11位指数位采用移码表示，可以表示正数、负数和零。52位尾数位、包括整数部分和小数部分，用于保存有效数字和精度。

这两种浮点数格式使用指数和尾数的组合方式，可以表达一定范围内的实数。浮点数格式的设计中，采用了阶码和尾数的分离表示方法，从而可以根据指数高低位的变化来动态调整浮点数的精度和范围，提高了浮点数计算的灵活性和准确性。

误差的起源：

我们可以用这张图简单表示一下二进制的存储

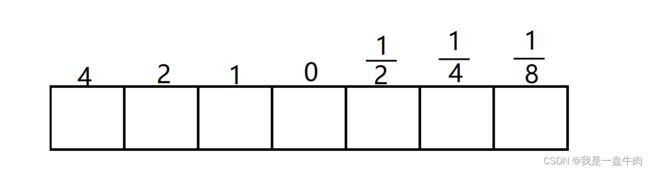
我们可看到：由于是二进制的原因，小数存储0.5，0.25非常方便，但是没有办法存储像0.1这样的数字，我们只能是无限逼近0.1，对应的二进制就是一个不断循环的无限数字：0.00011001100110011001100110011........ 

但是通过刚才对IEEE-754的介绍，大家应该已经清楚：我们能够存储的位数是有限的，如果是单精度浮点型，就只有23位存储空间，如果是双精度，就只有52位存储空间，因此像这种无限循环下去的二进制数字，在实际存储的时候就会被截断。而这也就是误差的来源。

虽然这种误差很小，但是在某些方面也会有很大的损失，例如银行的存储，如果银行每一份钱都要多出这么一点的话，那么对于银行来讲将会是巨大的损失。

因此我们也一直都在探寻如何避免浮点误差

如何避免浮点误差：

手动实现：

1. 不要直接比较浮点数
直接比较浮点数时，可能会因为浮点误差而得到错误的结果。而应该通过一个很小的误差范围来比较浮点数，例如相差小于某个很小数值 eps，则认为两个浮点数相等。

2. 尽可能使用整数运算
在一些情况下，可以预先将浮点数转换为整数，进行乘以若干倍数的运算，然后再除以对应的倍数，这样可以避免浮点误差。

3. 使用高精度算法
如果精度要求很高，可以使用高精度算法，例如可以使用自带高精度计算功能的编程语言，或者第三方高精度计算库等。

4. 设置适当的浮点数精度
有时可以使用四舍五入、向零取整等方式设置适当的精度来避免浮点误差。例如round函数，可以向最近的整数取整，也可以设置精度取小数点后几位

5. 避免迭代计算
迭代计算往往会引入严重的误差，因此应该尽可能避免使用。可以使用单次计算得到精确结果的方法来避免迭代计算。

最后需要说明的是，避免浮点误差的方法是应该根据具体问题来决定的，不同的问题可能需要不同的方法。在实际问题中，需要对精度和效率进行综合考虑，并选择适当的方法来避免浮点误差。

此外，Python还为我们提供了一个特殊的数据类型：deciaml，用来存储特定精度的小数。

ecimal是一个Python库，用于高精度浮点数计算。它允许开发者在不丧失精度的前提下进行浮点数运算。

ecimal库的主要特点如下：

1. 高精度
ecimal使用了基数为10的定点算术来执行浮点数运算，这使得它能够提供高达28位有效数字的计算。这就意味着，在进行涉及到小数点后多位数字的计算时，能够保持非常高的精度。

2. 可重现
与IEEE-754标准中指定的浮点数计算不同，ecimal的计算结果具有可重现性。这意味着无论使用何种计算机架构或CPU，则在每个机器上都将获得相同的结果。

3. 容易上手
由于模块的设计，使用ecimal库进行编码非常便捷。它可以很好地与Python的内置数据类型和运算符配合使用。而且，经过一些特殊的带符号的算术功能使得开发者可以控制精度。

        实际上，ecimal已经成为Python编程中十分重要的一个库，特别是在与商业、财务相关的计算中，例如货币兑换、税收计算等。在这些场景中，有必要保持高精度和可重现的浮点数计算，而ecimal正是提供这些功能的最佳解决方案之一。

 

回到刚开头的那个错误：既然不能直接比较，那么我们怎么办呢？

第一种方法是直接做差，当两个数的差很小的时候，我们就认为这两个浮点数相等。

自动实现：

第二种方法是直接调用各大语言里面的库函数，各语言在设计的时候就已经注意到了这个问题，因此已经设计好了库函数来供我们使用。

各编程语言提供的判断浮点数是否相等的函数如下：

1. Python：math.isclose()
在Python中，math.isclose()函数用来比较两个浮点数是否接近。该函数有五个参数，分别为a、b（需要进行比较的两个数）、rel_tol（相对误差阈值，默认为1e-9）、abs_tol（绝对误差阈值，默认为0）、两个布尔型参数，分别表示是否应考虑符号和两个值是否为NaN。当a和b之间的差异小于所提供的误差阈值时，该函数返回True，反之返回False。

2. C++：std::abs()
在C++中，可以使用std::abs()函数来判断两个浮点数是否相等。根据该函数返回的差值是否小于给定的epsilon，从而判断两个浮点数之间的差异是否小于阈值。例如：

   bool isEqual(double x, double y) {
       const double epsilon = 1e-9;
       if (std::abs(x - y) <= epsilon * std::abs(x)) {
           return true;
       }
       return false;
   }

3. Java：Math.abs()
在Java中，可以使用Math.abs()函数来判断两个浮点数是否相等。使用该函数返回的差值是否小于所给的epsilon值，从而判断两个浮点数之间的差异是否小于阈值。例如：

   public static boolean isEqual(double x, double y) {
       final double epsilon = 1e-9;
       return Math.abs(x - y) <= epsilon * Math.abs(x);
   }

4. MATLAB：eps()
在MATLAB中，可以使用eps()函数来判断两个浮点数是否相等。该函数返回与指定浮点数具有相同精度的浮点数。一般情况下，可以将浮点数进行相减并通过eps()函数计算差异，然后将结果与所给的epsilon值比较。例如：

   function bool = isEqual(x, y)
       epsilon = 1e-9;
       bool = abs(x - y) <= epsilon * abs(x);
   end

总之，使用这些函数可以有效地避免由于浮点舍入误差而导致不正确的计算结果。

 

 总结：

虽然浮点数会存在浮点误差的状态，但是我们不要害怕使用浮点数，只要在逻辑上牢记浮点数会出现浮点误差，就难出现错误。

如果我的内容对你有帮助，请点赞，评论，收藏。创作不易，大家的支持就是我坚持下去的动力！