Python之curve_fit多元函数拟合

入门

scipy.optimize中，curve_fit函数可调用非线性最小二乘法进行函数拟合，例如，现在有一个高斯函数想要被拟合

$$y=a\exp -(\frac{x-b}{c}{)}^2$$

则调用方法如下

import numpy as np
from scipy.optimize import curve_fit
def gauss(x, a, b, c):
    return a*np.exp(-(x-b)**2/c**2)

x = np.arange(100)/10
y = gauss(x, 2, 5, 3) + np.random.rand(100)/10

# 非线性拟合 abc为参数；para为拟合评价
abc, para = curve_fit(gauss, x, y)
print(abc)
# [2.03042233 5.01182397 3.10994351]

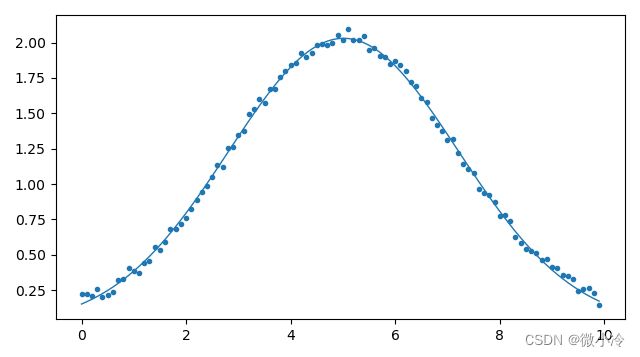
其中，curve_fit在调用时输入了三个参数，分别是拟合函数、自变量、因变量。返回值abc和para分别为拟合参数和拟合的协方差，最终得到abc的值与预设的2,0.5, 3是比较接近的，其拟合效果可以画图查看一下

import matplotlib.pyplot as plt
plt.scatter(x, y, marker='.')

Y = gauss(x, *abc)
plt.plot(x, Y, lw=1)
plt.show()

效果如下

参数

curve_fit的装形式如下

curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, **kwargs)

除了f, xdata, ydata已经用过之外，其他参数的含义为

• p0 拟合参数初始值
• sigma 相对精度要求
• absolute_sigma 绝对精度要求
• check_finite 有限性检测开关
• bounds 拟合范围
• method 拟合方法，可选‘lm’, ‘trf’, ‘dogbox’，与least_squares函数中定义相同
• jac 雅可比矩阵，与least_squares中定义相同

最小二乘函数：least_squares

多元拟合

尽管curve_fit的参数列表中，只给出了xdata, ydata作为拟合参数，而xdata只有一组，但curve_fit是具备多元拟合潜力的。

唯一需要注意的是，当多元拟合函数的返回值必须为一维数组，示例如下

# 创建一个函数模型用来生成数据
def func1(x, a, b, c, d):
    r = a * np.exp(-((x[0] - b) ** 2 + (x[1] - d) ** 2) / (2 * c ** 2))
    return r.ravel()
 
# 生成原始数据
xx = np.indices([10, 10])
z = func1(xx, 10, 5, 2, 5) + np.random.normal(size=100)/100
abcd, para = curve_fit(func1, xx, z)
print(abcd)
# [10.00258587  5.00146314  1.99952885  5.00138184]

可以发现拟合结果与预设的abcd还是比较接近的，下面绘制三维图像来更加直观地查看一下

z = z.reshape(10, 10)
Z = func1(xx, *abcd).reshape(10,10)

ax = plt.subplot(projection='3d')
ax.scatter3D(xx[0], xx[1], z, color='red')
ax.plot_surface(xx[0], xx[1], Z, cmap='rainbow')
plt.show()

结果如下