【python自定义函数多元拟合】拟合圆柱体方程

做这个原由

本人工作需要，要对厂房扫出来的三维点阵模型进行一些数值计算，比如说两个圆柱结构之间的同心度。
原本的计算方法是在圆柱上选择3个点，由三个点确定一个圆，进而确定圆心在哪里，然后对比两个圆心位置的差当作同心度的误差。
但是这种方法容易出错，因为选择的三个点不一定会在同一个垂直于圆柱的平面内，因此确定的圆心不一定就在圆柱的轴线上；此外，这种方法也不能确定圆柱轴线的方向。
因此，现在需要改进计算方式，选择圆柱表面上的点，收集其坐标，对这些点进行拟合，将其拟合在一个柱子的柱面上。拟合的结果确定的轴线位置和方向就能极大地提高同心度的计算

直角坐标确定轴线的拟合

拟合方程：样本点到直线的距离减去圆柱半径
所以带入每个样本就是（xi,yi,zi,0)，也就是点到圆柱轴线距离减圆柱半径=0，以此方法进行拟合。
点到直线距离使用公式：

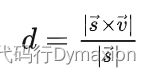
s为直线方向向量，v为点到直线上一点的矢量。

然后部分拟合数据如下：

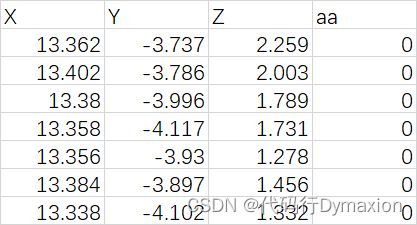
代码如下（没学过numpy，所以这个向量积的模是自己手搓的）：

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit

# 启动3d画图区域
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 定义拟合函数：样本点坐标lc，到圆柱轴线（点(x0,y0,z0)斜(a,b,c)式方程）的距离与圆柱半径的差
def di2line(lc,a,b,c,x0,y0,z0,r):
  return (((lc[1]-y0)*c-(lc[2]-z0)*b)**2
         +((lc[2]-z0)*a-(lc[0]-x0)*c)**2
         +((lc[0]-x0)*b-(lc[1]-y0)*a)**2
         )**0.5/(a**2+b**2+c**2)**0.5-r

# 读取数据
path='C:/Users/mllzq/Desktop/zhuzidedian.csv'
lss=np.array(np.loadtxt(path,dtype=float,delimiter=',',skiprows=1,usecols=(0,1,2),encoding='utf-8'))
arrx=np.array(np.loadtxt(path,dtype=float,delimiter=',',skiprows=1,usecols=0,encoding='utf-8'))
arry=np.array(np.loadtxt(path,dtype=float,delimiter=',',skiprows=1,usecols=1,encoding='utf-8'))
arrz=np.array(np.loadtxt(path,dtype=float,delimiter=',',skiprows=1,usecols=2,encoding='utf-8'))
arr4=np.array(np.loadtxt(path,dtype=float,delimiter=',',skiprows=1,usecols=3,encoding='utf-8'))
arrs=np.array([arrx, arry, arrz])

# 拟合
# p0是初始值，一定要给出，不然会拟合到圆柱外面
# bounds是拟合值的边界，最好也给出
popt, pcov = curve_fit(di2line, arrs, arr4, 
                      p0=     [0.81, 3.827, 0   , 10.493, -5.708, 1.677, 2.5],
                      bounds=[(0.3, 0.555, -0.5, 10.000, -6.000, 1.000, 0), (0.99, 4.555, 0.5 , 11.555, -4.000, 2.000, 10)]
                      )
print(popt)


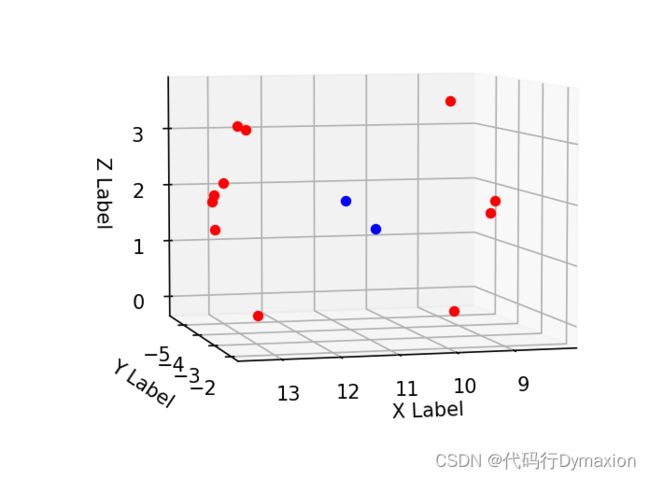
# 绘制样本点（部分）和轴线上两点
for i in range(11):
  loc=lss[20*i]
  ax.scatter(loc[0], loc[1], loc[2], c='r', marker='o')
ax.scatter(popt[3], popt[4], popt[5], c='b')
ax.scatter(popt[3]+popt[0], popt[4]+popt[1], popt[5]+popt[2], c='b')

ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()

结果：

[ 8.13055531e-01  3.81320083e+00  8.60751696e-04  1.04974355e+01
 -5.69881713e+00  1.67535619e+00  2.46670373e+00]
[Finished in 51.6s]

或极坐标确定轴线进行拟合（减少方程自由度的思路，未完成）

以上的方法，用三个值确定方向向量、三个值确定轴线上一点，加上圆柱半径总共7个自由度，以此确定了直线方程。但是这种方法多了两个自由度，这种情况可能影响准确性，我尝试使用极坐标让整体自由度降至5：

θ和φ确定轴线的方向；
α确定轴线移动方向，这个移动方向是在垂直于轴线方向的平面内确定的，因此只需要一个自由角度；
di是轴线移动距离。

因此，空间任意直线都与这四个值是一一对应的：即任意直线都能看作经过原点的直线向垂直于直线方向平移后得到的。
再加上圆柱半径，也就5个自由度就够了。
代码如下：

# 极坐标转直角坐标
def sephere(th, ph, di):
  a=di*np.sin(th)*np.cos(ph)
  b=di*np.sin(th)*np.sin(ph)
  c=di*np.cos(th)
  return [a,b,c]

# 极坐标直线转化为直角坐标直线（增加了两个自由度）
# th in [-0.5pi, 0.5pi], ph in [0, pi], al in [-0.5pi, 0.5pi], di in R
def LineBySephere(th, ph, al, di):
  on=sephere(th, ph, 1)
  oa=sephere(
             -np.arccos(np.sin(th)*np.cos(al)), 
              np.arctan(np.tan(al)/np.cos(th))+ph, 
              di
            )
  return [on, oa]

# 直角坐标直线转化为极坐标直线（减少了两个自由度）
def antilbs(xn,yn,zn,xa,ya,za):
  rn=(xn**2+yn**2+zn**2)**0.5
  if zn<0:
    rn=-rn
  xn=xn/rn
  yn=yn/rn
  zn=zn/rn
  th=np.arccos(zn)
  if yn<0:
    th=-th
  if xn==0:
    ph=0.5*np.pi
  else:
    ph=np.arctan(yn/xn)
  if ph<0:
    ph+=np.pi
  k=-xn*xa-yn*ya-zn*za
  xa=xa+k*xn
  ya=ya+k*yn
  za=za+k*zn
  ax.scatter(xa, ya, za, c='b')
  di=(xa**2+ya**2+za**2)**0.5
  if xa+ya*np.tan(ph)==0:
    al=0.5*np.pi
  else:
    al=np.arctan(np.cos(th)*(ya-xa*np.tan(ph))/(xa+ya*np.tan(ph)))
  if xa==0:
    php=0.5*np.pi
  else:
    php=np.arctan(ya/xa)
  if xa<0:
    php+=np.pi
  if np.cos(php-ph)>0:
    di=-di
  xa=xa/di
  ya=ya/di
  za=za/di
  ax.scatter(xa*di, ya*di, za*di, c='b')
  return [th, ph, al, di]

如果不需要拟合初始值p0，可以不需要直角坐标系直线转化为极坐标系直线，但这却是必要的，不然会拟合在样本点群的外面；而且，我写的这个方程在一些边界值的情况下有些问题，有待进一步优化。