动态规划之解码方法
1. 题目分析
题目链接选自力扣 : 解码方法

根据题目要求, 实现了一个编码的映射关系, 也就是 A ~ Z 的 26 个大写字母分别对应着 1 ~ 26 的数字. 依据例子 “11106” 来进行分析 :
- 整个字符串单独划分每个位置的字符
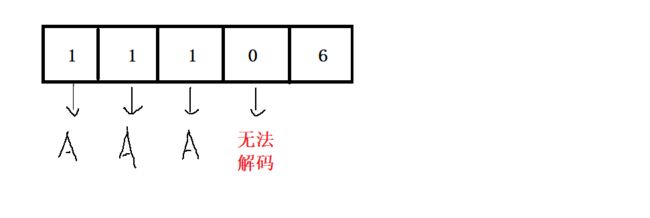
单独划分的情况下, 出现了 0 导致整个字符串无法解码成功. 因此有 0 时是无法单独划分一个字符解码的.
- 整个字符串中某个位置和这个位置前后的字符合并两个字符解码

这种情况下, 前后两个位置互相组合, 并且组合成的字符数字大小范围在 1 ~ 26 以内, 则可以解码.

而这种划分情况下, 出现了 "06’ 的组合, 而它在映射关系中是没有对应的字母可以对应的. 因此是无法正确解码的.
总结一下什么时候无法解码呢 ?
- 当两个位置的字符出现前置 0 时无法解码, 例如 “06”
- 当两个位置的字符大小超过 26 时无法解码, 例如 “27”
- 当某个位置出现 0 时, 整个字符串不能单独划分解码.
2. 状态表示
以 i 位置为结尾时, 表示从第一个位置解码到 i 位置时一共对应多少种解码方法.
因此 dp[i] 即表示从字符串起始位置解码到 i 位置时对应的解码方法数.
3. 状态转移方程
对于这种一维的线性表, 一般使用最近的一步来解决. 什么是最近一步呢 ?
在这个问题里, 当求解 dp[i] 时, 分两种情况.
- 当 i 位置可以单独解码时.
- i 位置单独解码成功时, 也就是 i 位置对应的字符大小范围在 1 ~ 9 之间, 那么这时候的解码总数为多少呢 ?
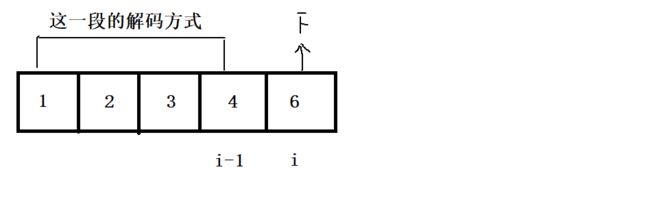
可以看到, 起始位置到 i - 1 位置无论他是解析成 " 1 "2 " “3” “4” 还是 “12” “3” “4”, 当 i 位置解码成功时最后的结果都需要加上这个位置的 “F”, 也就是 " 1 "2 " “3” “4” + “6 " 解码为 “ABCDF”. 而"12” “3” “4” + “6” 解码为 “LCDF”.
最终的解码数也是从起始位置到 i - 1 位置的解码总数. 正好对应着我们转态表示所描述的, 结果为 dp[i-1]
- i 位置单独解码不成功时, 也就是 i 位置对应的字符大小范围不在 1 ~ 9 之间 ( 基本确定为字符 0 )
当 i 位置无法单独解码时, 此时前面从起始位置到 i - 1 无论有多少种方法, 最后面 i 位置无法解码都会让整个字符串无法解码. 因此其解码总数结果为 0.
例如 " 12 " “3” “4” “0”. 最后这个 0 时无法解码的. 前面的"1234" 无论你如何组合最终都无法解码.
- 当 i 位置和 i - 1 位置合并解码时
- 当 i 位置和 i - 1 位置合并后可以成功解码, 也就是两个位置组成的字符大小为 i-1 对应的字符 a * 10 + i 位置对应的字符 b 的大小范围在 10 ~ 26 以内.
这时候的解码总数又为多少呢 ?

这时候, i - 1 位置和 i 合并后, 组成了 “12” 对应解码后为 “L”. 前面的字符串"123" 无论怎么组合, 例如"1" “23” 还是"12" “3”, 最终的解码都为"1" “23” “12” 对应解码后为 “AWL”. “12” “3” “12” 对应解码后为 “LCL”. 因此解码的总数取决于从起始位置到达 i - 2 位置的解码总数. 正好对应我们的状态表示, 因此最终这种情况下的解码总数为 dp[i-2]
- i 位置和 i - 1 位置合并后的字符大小不在 10- ~ 26 范围内, 无法解码
同样的, 当 i - 1 和 i 位置无法解码时, 无论前面如何组合出几种解码方式, 最终都是无法解码的. 因此解码总数为 0
最终我们的状态转移方程为 : dp[i] = dp[i - 1] + dp[i - 2]
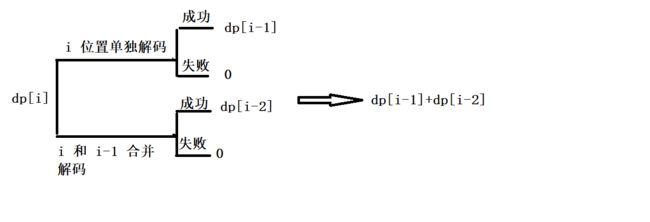
4. 初始化
初始化防止我们在填写 dp 表示出现越界情况, 从上面的状态转移方程不难看出, 我们需要单独处理 dp[0] 和 dp[1] 位置的解码数
dp[0]时, 意味着只有一个字符.
- 如果它对应的字符大小不为 ‘0’, 那么它就一定对应 A ~ J 中的某个字母. 因此总数为 1. dp[0] = 1
- 当它大小为 ‘0’ 时, 无法解码, 总数为 0. dp[0] 在 dp 表中默认为 0, 无需初始化
dp[1]时, 自个字符串一共有两个字符.
- 0 位置和 1 位置无法单独解码, 合并后字符大小不在 10 ~ 26之间, 例如 “05”, “27”. 解码数为 0. 此时 dp[0] 在 dp 表中默认为 0, 无需初始化
- 0 位置和 1 位置都可以单独解码. 但合并后无法解码. 例如 “27” 解码数为 1.
条件为 : s[0] != ‘0’ & s[1] != ‘0’ , 此时 dp[1] = 1
- 0 位置和 1 位置可以单独解码, 并且合并后也可以解码. 例如字符串"12", 解码成"1" “2” 或者 “12”. 解码数为 2
条件为 : sum = s[0] * 10 - ‘0’ + s[1] - ‘0’ 计算出两个合并后的字符大小, 10<= sum <=26, 此时 dp[1] = 2
5. 调表顺序
从上面的状态转移方程不难看出, 当想要求解 dp[i] 时, 必须要先知道 dp[i - 1] 和 dp[i - 2], 也就是前两个位置的解码总数. 因此填表顺序是从左往右
6. 确认返回值
题目要求解码到字符串的最后一个位置. 而字符串的最后一个位置则是 n-1, 对应到我们的转态表示中则是 dp[n-1]
7. 代码演示
class Solution {
public int numDecodings(String ss) {
char[] s = ss.toCharArray(); // 转为字符数组方便取字符
// 1. 创建 dp 表
int n = ss.length();
int[] dp = new int[n];
// 2. 初始化
// 一个字符如果不为'0'时一定有一种解法
if(s[0] != '0') dp[0] = 1;
// 特殊情况处理, 注意到 1 <= n < 100, 当 n 为 1 时是无法初始化 dp[1] 的
// 只有一个字符, 返回 dp[0] 代表 0 位置的字符解码总数
if(n == 1) return dp[0];
// 两个字符可以单独解码时
if(s[0] !='0' && s[1] != '0') dp[1] += 1;
// 两个字符还可以合并后解码
int sum = (s[0] - '0') * 10 + s[1] - '0';
if(sum >= 10 && sum <= 26) dp[1] += 1;
// 3. 填写 dp 表, dp[i] 为两种情况的解码数之和
for(int i = 2; i < n; i++) {
// i 位置单独解码成功时
if(s[i] != '0') dp[i] += dp[i -1];
// i 和 i-1 位置合并解码成功时
int sum2 = (s[i - 1] - '0') * 10 + s[i] - '0';
if(sum2 >= 10 && sum2 <= 26) dp[i] += dp[i - 2];
}
// 4. 确认返回值
return dp[n - 1];
}
}
8. 解法二
8.1 对初始化代码的优化
上面初始化过程中, 对于 dp[1] 进行初始化时, 特别的麻烦. 因此我们考虑有没有别的方式来简化这个初始化. 从而我们引出了下面这种方式. 建立一个新的 dp 表, 大小为 n + 1, 将旧 dp 表中 0 下标的值放到新 dp 表中 1 下标处. 旧 dp 表中 1 下标的值放到新 dp 表中 2 下标处.
这样在填表的时候, 从 i = 2 开始就不用去初始化 dp[1] 了. 因为 旧 dp[1] 已经到新 dp[2] 位置去了. 填写新 dp 表时, 就不再需要初始化 dp[1] 这么麻烦了.
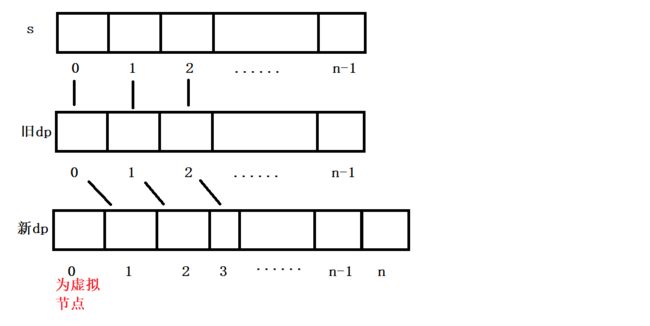
引入这个新的 dp 表后, 会发现多了 0 下标的值, 那么这个位置的值该是多少呢 ?
根据状态转移方程 计算 dp[2] 时, 需要计算 dp[0] 和 dp[1]. 而 dp[1] 对应旧的 dp 表中的 dp[0], 这个是很容易初始化的. 那么 dp[0] 就是影响 dp[2] 结果的最大因素.
从状态转移方程 dp[i] = dp[i-2] + dp[i-1] 知道, 当 dp[2] 需要使用到 dp[0] 时, 一定是 0 位置和 1 位置合并后有一种解码方式.

当 dp[0] = 0 时, 说明合并后解码失败. 本身 dp[0] 不初始化默认也是 0. 当使用到dp[0]时一定是 0 下标和 1 下标合并后可以解码. 因此 dp[0] 最终的初始化一定是 1.
8.1 返回值
原本的字符串长度为 n - 1 . 也就是只需要返回从起始位置到 n -1 位置结束时的解码总数. 对应到状态方程中也就是我们的 dp[n - 1]. 由于我们这个新的 dp 表长度为 n + 1. 原本 n - 1 的位置+1 后对应到 n 的位置. 因此最终返回值为 dp[n]
8.2 代码演示
class Solution {
public int numDecodings(String ss) {
char[] s = ss.toCharArray(); // 转为字符数组方便取字符
// 1. 创建 dp 表
int n = ss.length();
int[] dp = new int[n + 1];
// 初始化dp[0], 以保证后续填表正确
// 经过分析, 当使用到 dp[0] 时, 必然是 0 和 1 位置合并后可以解码. 必有一种解码数
dp[0] = 1;
// 2. 初始化 dp[1], 也就是旧 dp表的 dp[0] 位置.
// 新表的 1 下标对应旧表的 0 下标, 因此获取字符时, 每个位置都需要 -1
if(s[1-1] != '0') dp[1] = 1;
// 3. 填写 dp 表, dp[i] 为两种情况的解码数之和
for(int i = 2; i < n + 1; i++) {
// i 位置单独解码成功时
if(s[i - 1] != '0') dp[i] += dp[i -1];
// i 和 i-1 位置合并解码成功时
int sum2 = (s[i - 1 - 1] - '0') * 10 + s[i - 1] - '0';
if(sum2 >= 10 && sum2 <= 26) dp[i] += dp[i - 2];
}
// 4. 确认返回值
return dp[n];
}
}