一种快速的幂运算方法（底数是自然数e，指数是浮点数）

问题

  【给一个浮点数 $y$，现在需要你求出 $e^y$ 的值是多少】。

  对于这个问题，最直接的方法是用库函数，例如在C++中头文件提供了exp()函数，Python里通过import math使用math.exp()。这些方法精度较高，但是速度相当慢。。

  在深度学习（DeepLearning）中经常需要花费大量时间进行幂运算，典型场景是使用激活函数和计算概率分布的时候。例如在 SoftMax 层通常需要进行底数是 $e$ ，指数是浮点数的幂运算。

  提高幂运算的速度，能有效提高实际应用的速度。据说一些消费级的NVIDIA显卡都是把双精度给砍了，有时候你甚至是用半精度在训练。对于大多数神经网络计算而言，近似精度是完全足够的，并且可以节省很多时间。

方法

  有一些其它的快速幂运算方法，如查找表，使用线性插值等。
  这里参考文章《A Fast, Compact Approximation of the Exponential Function》的方法，能够以较少的精度损失换取明显的速度提升。
  经我测试，速度比库函数快几倍到几十倍，具体看指数有多复杂。据说在某些特定的值上误差范围有 $\pm 10\%$，这个看你如何权衡精度与速度。

  假设目标机器是大端字节序，double类型为64位，float类型为32位，int类型为32位，short类型为32位。

double版本：

（version1）

inline double fast_exp(double y){
    union{
        double d;
        int x[2];
    }data = {y};
    
    data.x[0] = 0;
    data.x[1] = (int)(y * 1512775 + 1072632447);
    
    return data.d;
}

（version2）

inline double fast_exp(double y){
    double d;
    *(reinterpret_cast<int*>(&d) + 0) = 0;
    *(reinterpret_cast<int*>(&d) + 1) = static_cast<int>(y * 1512775  + 1072632447);
    return d;
}

  以上两段代码意思是一样的，只是实现方式不一样。
  (version1)用联合体是为了能分别拿到一块64位数据的高32位和低32位，(version2)通过修改指针的类型，也是为了拿到高位和低位。

float版本：

（version1）

inline float fast_exp(float y) {
    float d;
    *(reinterpret_cast<short*>(&d) + 0) = 0;
    *(reinterpret_cast<short*>(&d) + 1) = static_cast<short>(184 * y + (16256-7));
    return d;
}

  因为在Cortex-A7的Neon Intrinsics中没有双精度浮点数的类型，只能用到float，所以我参考别人的文章写了一个float版本的实现，以便使用Neon加速计算。

（version2） 参考自https://www.itread01.com/content/1550634858.html ，尚未验证

union
{
    uint32_t i;
    float f;
}v;
v.i=(1<<23)*(1.4426950409*val+126.94201519f);
return v.f;

原理

  根据IEEE754-1985标准（IEEE Standard for Binary Floating-Point Arithmetic），一个浮点数可以通常用以下形式表示：

$$(-1{)}^s\cdot (1+m)\cdot 2^{x-x_0}$$

公式1

  其中 $s$ 是符号位，$m$ 是尾数（一串内存里的二进制的数字），$x$ 是指数项，$x_0$是偏置（bias）。

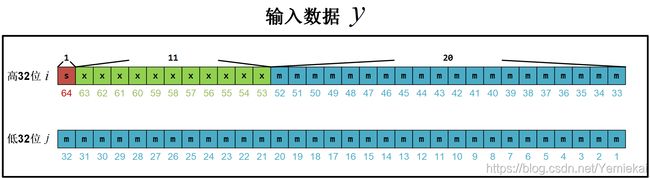
  对于一个64位的浮点数，尾数 $m$ 占52位，指数项 $x$ 占11位，偏置 $x_0=1023$，在内存空间占8个字节：

(图1) 双精度浮点数的内存排列

以上是浮点数的表示法及其数据存放特点。 先记住。

然后… 先来看看 $2^y$ 怎么求：
  现在输入一个浮点数 $y$，你需要计算 $2^y$。
  $y$ 是一个浮点数，它的表达式为 $y=(-1{)}^s\cdot (1+m)\cdot 2^{x-x_0}$。观察发现，$y$ 的表达式里面就含有2次幂 “$2^{x-x_0}$” ，我们正好需要计算2次幂，把 $x-x_0$ 换成 $y$ 不就行了？妙啊。

  上面讲了思路，具体怎么操作呢？看回图1，指数项 $x$ 在内存的[53~63]位，把 $y$ 放到对应的位上面，就完成了替换。

(图2) 和图1一样的意思

  首先把 $y$ 当成int数，然后加上 $x_0$，也就是 $y+1023$（根据规范，双精度浮点数的偏置项bias是 $x_0=1023$）（可能加上 $x_0$ 是为了消掉 $x-x_0$ 中的 $x_0$，把 $2^{x-x_0}$ 变成 $2^y$ ）。
  然后把结果左移20位（乘以 $2^{20}$），就对应到指数项所在的坑（图2中绿色格子），由此把指数项换成了 $y$。
  结合上述步骤，求 $2^y$ 的方法就是：取出 $y$ 的高32位（图1中的 $i$），让它等于 $2^{20}\cdot (y+1023)$ 即可。得到的结果就是 $(-1{)}^s\cdot (1+m)\cdot 2^y$，这里还有 $m$，后面再讲怎么处理。


  通用表达式是： 令 $y$ 的高32位 $i=ay+(b-c)$

  求 $e^y$ 的时候，式中 $a=2^{20}/ln(2)$，$b=1023\cdot 2^{20}$，$c$ 的经验值是 $60801$ ，$c$ 是用于减少误差的。

  为什么 $a$ 是这个值，不是 $2^{20}$ 吗。因为这是在求 $e^y$ 。前面原理讲是针对 $2^y$ 讲的，求 $e^y$ 的时候需要变一下，看下面的推导：
$$2^a=e^{ln{2}^a}=e^{a\cdot ln2}$$

  令 $y=a\cdot ln2$，则 $a=y\cdot \frac{1}{ln2}$，上面的式子变成：
$$2^{y\cdot \frac{1}{ln2}}=e^y$$

  $\frac{1}{ln2}$ 是一个常数，约为 $1.442695....$ ，因此 $e^y$ 可以通过求 $2^y$ 得到，过程是一样的，变换一下 $y$ ，把输入的 $y$ 乘上 $\frac{1}{ln2}$ 即可。

  $c$ 为什么是 $68243$， 这有点复杂，请看原文作者的推导。

所以：
  $a=2^{20}/ln(2)=1512775$ ，
  $(b-c)=1023\cdot 2^{20}-60801=1072632447$

就和代码里的数值对应上了(见double版本的version1)。
单精度的计算方法类似，根据单精度浮点数的存储方式改一下参数就可以了。

注意：
  这种快速幂运算的方法对输入数据 $y$ 是有要求的，对于double版本而言，输入 $y$ 大概要在 $[-700,700]$ 的区间，超出范围算法失效。对于float版本而言，在$[-10,10]$之间是没问题的。

  关于 $m$ ： 为什么代码里把低32位的数据置零，因为这一步是为了把公式1中的 $m$ 置零，保证只有指数项。再看图2，只是把低32位的 $m$ 置零了，高32位还有20个 $m$ 不用管？确实没有管，原文作者说保留这部分的 $m$ 不仅没什么影响，反而有助于提高精度。

总结

  上面的原理只是大概近似的理解，并不是很深刻。原文只讲述了做法和过程，给了一条公式，没有详细解释原因，我也没弄太懂。根据这种方法修改到float类型上也能work，看来原理是没问题的。有兴趣的可以再看看原文《A fast, compact approximation of the exponential function》。另外需要结合浮点数的原理，参考IEEE754规范《754-1985 - IEEE Standard for Binary Floating-Point Arithmetic》。

Reference

《这个求指数函数exp()的快速近似方法的原理是什么?》
https://www.zhihu.com/question/51026869

《快速浮點數exp演算法》
https://www.itread01.com/content/1550634858.html

《Optimized pow() approximation for Java, C / C++, and C#》
https://martin.ankerl.com/2007/10/04/optimized-pow-approximation-for-java-and-c-c/