【MatLab】《遗传算法GA+BP神经网络——电路参数估计》
matlab语言 遗传算法GA+BP神经网络 电路参数估计
一、整体设计概述:BP神经网络代理电路模型 GA寻找误差最小参数
根据采样数据训练BP神经网络,用训练好的网络来作为目标函数输出电路参数误差,通过GA寻找误差最小的电路参数值。

二、代码实现(需要完整代码的私聊)
BP.m 主函数
clc
close all
clear all
%% 训练BP模型
datapath='f=85000.xls';
f=85000;
% datapath='f=6.393341925217580e+04.xls';
myBP=BPMod(datapath);
%% 使用BP模型预测
Iin_cl=16.54;
Icf_cl=19.28;
[M_pre,RL_pre]=mypredictor(myBP,Iin_cl,Icf_cl);
[Iin_exp,Icf_exp]=get_expI(f,M_pre,RL_pre);
disp(['Iin测量值为:',num2str(Iin_cl)])
disp(['Icf测量值为:',num2str(Icf_cl)])
error=abs(Iin_cl-Iin_exp)+abs(Icf_cl-Icf_exp);
disp(['最小误差为:',num2str(error)])
disp(['M预测值为:',num2str(M_pre)])
disp(['RL预测值为:',num2str(RL_pre)])
disp(['Iin计算值为:',num2str(Iin_exp)])
disp(['Icf计算值为:',num2str(Icf_exp)])
BPMod.m 数据处理+训练BP网络
function myBP=BPMod(datapath)
%% 数据预处理
% datapath='f=85000.xls';
data=xlsread(datapath);
trainRatio=0.75;
valRatio=0;
testRatio=1-trainRatio;
[trainInd,valInd,testInd] = dividerand(max(size(data)),trainRatio,valRatio,testRatio);
input_train=data(trainInd,3:4);
output_train=data(trainInd,1:2);
input_test=data(testInd,3:4)';
output_test=data(testInd,1:2)';
% %% 数据归一化
% for i=1:size(output_train,2)
% output_train(:,i)=mymaxminmap(output_train(:,i));
% end
%% 输入输出数据归一化
[inputn,inputps]=mapminmax(input_train');
[outputn,outputps]=mapminmax(output_train');
% outputn=outputn';
%% BP网络训练
node_in_num=2; % 输入层节点数量
% node_hidden_num=2*node_in_num+1;% 隐含层节点数量
node_out_num=2;
node_hidden_num=(node_out_num+node_in_num)+randi([1,10]);% 隐含层节点数量
% %初始化网络结构
% net=newff(inputn,outputn,node_hidden_num);
net=feedforwardnet(11,'trainlm');
net.trainParam.epochs=10000;
net.trainParam.lr=0.01;
net.trainParam.goal=0.0002;
net.trainParam.showCommandLine=true;
net.trainParam.max_fail = 20;
% net.divideFcn='divideind';
% net.trainParam.showWindow=true;
%网络训练
net=train(net,inputn,outputn);
%% BP网络预测
%预测数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
%网络预测输出
an=sim(net,inputn_test);
%网络输出反归一化
BPoutput=mapminmax('reverse',an,outputps);
%%
figure
subplot(2,1,1)
plot(BPoutput(1,:),'r*')
hold on
plot(output_test(1,:),'bo')
plot(abs(BPoutput(1,:)-output_test(1,:)),'c--.')
legend('BP预测值','实际值','误差绝对值')
title('Iin')
grid on
subplot(2,1,2)
plot(BPoutput(2,:),'r*')
hold on
plot(output_test(2,:),'bo')
hold on
plot(abs(BPoutput(2,:)-output_test(2,:)),'c--.')
legend('BP预测值','实际值','误差绝对值')
title('Icf')
grid on
[c,l]=size(BPoutput);
error=abs(BPoutput(2,:)-output_test(2,:))+...
abs(BPoutput(1,:)-output_test(1,:));
MAE1=sum(abs(error))/l;
MSE1=error*error'/l;
RMSE1=MSE1^(1/2);
disp(['-----------------------误差计算--------------------------'])
disp(['隐含层节点数为',num2str(node_hidden_num),'时的误差结果如下:'])
disp(['平均绝对误差MAE为:',num2str(MAE1)])
disp(['均方误差MSE为: ',num2str(MSE1)])
disp(['均方根误差RMSE为: ',num2str(RMSE1)])
myBP.inputps=inputps;
myBP.net=net;
myBP.outputps=outputps;
% f=85000;
% RL=50;
% M=5.477e-5;
% % [Iin_exp,Icf_exp]=get_expI(f,M,RL);
% %
% fitness=getfitness(myBP,f,M,RL);
GA.m 遗传算法主函数
clc
close all
clear all
%% 模型参数
f=85000;
RL_max=200;
RL_min=50;
M_max=1e-4;
M_min=1e-5;
Iin_cl=16.54;
Icf_cl=19.28;
%% GA参数设置
Maxgen=1000;
Popnum=50;
Pc=0.5;
Pm=0.5;
%% 初始化种群
for i=1:Popnum
chrom(i).M=(M_max-M_min)*rand()+M_min;
chrom(i).RL=(RL_max-RL_min)*rand()+RL_min;
chrom(i).fitness=getfitness(f,Iin_cl,Icf_cl,chrom(i).M,chrom(i).RL);
end
%% 种群进化
gen=0;
while gen三、结果展示
BP神经网络训练情况
本模型使用BP神经网络来代理实际电路的输出,因此神经网络的回归效果一定要好,预测结果贴近实际电路输出,这样才能确保后续参数寻优的准确性
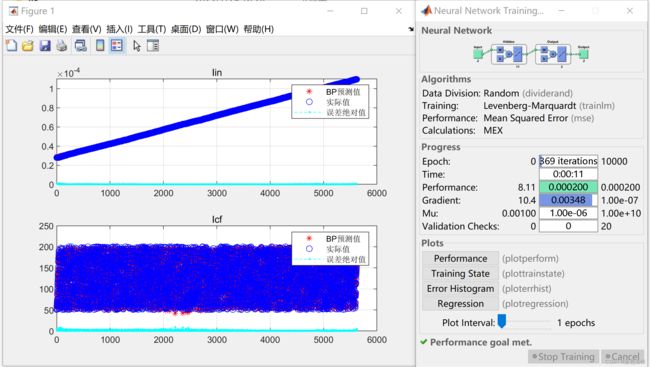
遗传算法优化结果
以电路参数误差为目标函数,通过GA+bp模型 找到最优的参数。
一是通过进化曲线,确认GA算法已经收敛,如果不收敛的话就调整GA的参数,使得在迭代后期目标函数值趋于稳定。


可以看到BP模型的预测值和实际值很接近,说明BP神经网络训练效果较好,最终误差为0.53179,对应的电路参数M和RL也通过GA得到。
四、项目分享
源码链接:C币下载
需要免费分享的关注+点赞+收藏的 私聊领取
完整的项目内容
包含:
**模型文件和电路数据
BP模型代码
GA模型代码
均可分别运行
内含simulink封装好的S函数 可以支持simulink使用
可以结合这个案例,学习遗传算法和BP神经网络的单独使用的方法,以及遗传算法+BP代理模型联合仿真的方法,如果你的问题是电路参数估计的模型,更改数据和公式之后可以直接使用
