双向交错CCM图腾柱无桥单相PFC学习仿真与实现（2）SOGI_PLL学习仿真总结

目录

前言

SOGI基本原理

锁相环基本原理

仿真实现及说明

总结

---

前言

前面总结了双向交错CCM图腾柱无桥单相PFC系统实现，后面把问题细分，关于SOGI锁相环的应用和学习在这里总结下。

双向交错CCM图腾柱无桥单相PFC学习仿真与实现（1）系统问题分解_卡洛斯伊的博客-CSDN博客

SOGI基本原理

SOGI也叫做二阶广义积分器，也叫正交信号发生器，目的就是得到单相的正交信号，其实说白了就是相当于一个观测器，通过SOGI之后得到电网侧的电压（幅值）和相位，如下图是TI的文档摘录下来的框图：

V'估算的同相位的电网电压

qv'相位相差90度

参考文档： Software Phase Locked Loop Design Using C2000™ Microcontrollers for Single Phase Grid Connected Inverter

 为了方便理解，直接定义V' 为valpha, qv'为vbeta：从输入Vin到输出的传递函数可以表示如下，从上面的框图很容易就推导出来了，很多论文也都是这个表达式：

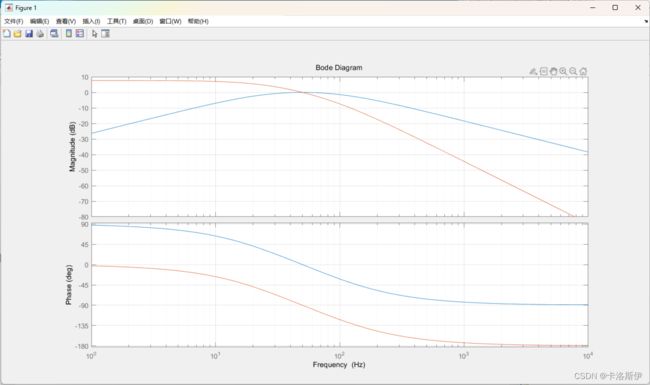
 在Matlab里面创建脚本来帮助分析它们的传递函数，电网频率50Hz，K取1.414如下：

 

 上图时k=1.414时，传递函数Valpha和Vbeta的频率响应曲线。当输入信号在50Hz时，有频率响应曲线可分析得出：增益 为0 db, 表明输出信号alpha和beta在50Hz幅度保持不变。相位在50Hz处：Valpha是0度，表示alpha成输入同相位，Vbeta是-90度，表示beta的输入滞后输入90度。另外，谐波次数越高，该系统对谐波的衰减作用越大。

 改变k=0.414的值：

 改变k=2.414的值：

 从上图可以看出，K的值越大对高次谐波的抑制越小，通过的频率只与Wn有关

再看下三者的阶跃响应：

K越小，响应越快稳定性越差，K越大响应越慢，稳定性越好，综合下来K取1.414或者1附近都是可以的，具体也要看电网谐波情况和响应需要选择合适的值

 K值影响的就是Valpha观测的响应速度：

K=0.9

 K=1.414

锁相环基本原理

前面介绍了SOGI的原理，接下来如何设计锁相环，通过SOGI得到了Valpha,Vbeta,当稳态时有：

 经过Clark变换后有：

 通过上式可以看出，当估算角度和实际角度一样时，利用这个特性，就可以设计出锁相环，把当作锁相环的误差输入, 除以相当于把输入误差归一化. 当估计角度接近实际角度, 可直接表示为:

 这时候控制框图可等效为:

 根据框图设计锁相环参数:

 PLL_KP=33.3;
 PLL_Ki=33.3*3;
 W0sogi= 2*pi*50;
 C_PLL_s=PLL_KP+(PLL_Ki/s)+W0sogi;
 G_PLL_s=1/s;
 controlSystemDesigner( G_PLL_s,C_PLL_s,1,1); 

带宽50Hz

锁相环输出的频率, 这里对比了锁相环带宽50Hz和100Hz参数的估算的电频率的响应(电网频率50Hz).

仿真实现及说明

根据前面的理论, 搭建SOGI_PLL的仿真模型

1.模拟电网电压,这里添加了357次谐波来验证SOGI的特性

2.SOGI估算电网电压和正交的电网电压

3.利用Park变换设计的锁相环

4.计算电压RMS的值

仿真效果:

黄色Vbase相当于实际的电网电压(理想电压), 蓝色Vin叠加了各种高次谐波, 经过SOGI后得到的估算电网电压和Vbase重合,避免高次谐波的干扰.

 完整的仿真过程如下:

总结

以上, 根据个人的理解并构建了相应的仿真模型验证, 并解释了SOGI_PLL参数的特性和如何设计对应的参数。参考模型：

https://download.csdn.net/download/weixin_42665184/87936402?spm=1001.2014.3001.5503