【算法总结】——排列型回溯

排列型回溯

相比于组合，排列型回溯对于元素的顺序是有要求的。

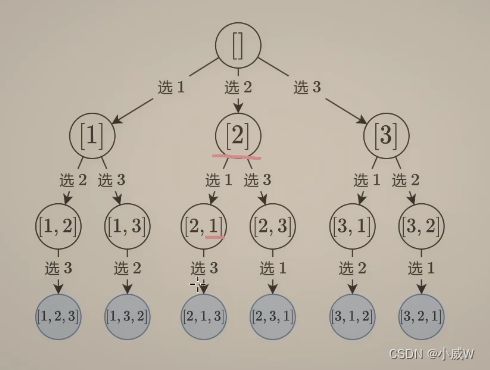
为了告诉回溯下面还可以选择哪些数字，可以：

1. 记录已经被选择的数字
2. 用一个集合存储还可以被选择的数字

---

对于排列型回溯，（与其他类型回溯的主要区别就在于 需要额外的记录）

例题1——46. 全排列

https://leetcode.cn/problems/permutations/

依次尝试各个位置上放置哪个数字，同时记录哪些数字是已经被放置过了的。

class Solution {
    List<List<Integer>> ans = new ArrayList();
    List<Integer> t = new LinkedList();

    public List<List<Integer>> permute(int[] nums) {
        int n = nums.length;
        boolean[] st = new boolean[n];  // 记录第i个数是否已经被选过
        dfs(nums, st, 0);   // 第0个位置放置哪个数字
        return ans;
    }

    public void dfs(int[] nums, boolean[] st, int k) {
        if (k == nums.length) {
            ans.add(new ArrayList(t));
            return;
        }
        for (int i = 0; i < nums.length; ++i) { // 依次尝试各个数字放在第k个位置
            if (st[i]) continue;
            st[i] = true;
            t.add(nums[i]);
            dfs(nums, st, k + 1);
            st[i] = false;	// 恢复现场
            t.remove(t.size() - 1);
        }
    }
}

除了额外声明一个 st数组 来记录每个数字的状态之外，还可以通过给 nums数组 中已经被选择的数字加上一个特别大的数字，这样如果一个数字超过了原本数据的范围，那么就表示它已经被选择过了。

例题2——N皇后

https://leetcode.cn/problems/n-queens/

class Solution {
    char[][] borad;
    Set<Integer> s1 = new HashSet(), s2 = new HashSet(), s3 = new HashSet();
    List<List<String>> ans = new ArrayList();

    public List<List<String>> solveNQueens(int n) {
        borad = new char[n][n];
        for (int i = 0; i < n; ++i) Arrays.fill(borad[i], '.');
        dfs(0, n);
        return ans;
    }   

    public void dfs(int row, int n) {
        if (row == n) {
            List<String> t = new ArrayList();
            for (char[] line: borad) t.add(new String(line));
            ans.add(t);
            return;
        }
        for (int i = 0; i < n; ++i) {   // 遍历这一行的每一列
            if (!s1.contains(i) && !s2.contains(i + row) && !s3.contains(i - row)) {
                s1.add(i);
                s2.add(i + row);
                s3.add(i - row);
                borad[row][i] = 'Q';
                dfs(row + 1, n);
                borad[row][i] = '.';
                s1.remove(i);
                s2.remove(i + row);
                s3.remove(i - row);
            }
        }
    }
}

同一 正斜线 和 反斜线 上的横纵坐标，他们的横纵坐标之和和之差分别是相同的。

除了使用 HashSet 来记录已经放置的情况外，还可以是用 boolean数组 来做记录。

这道题目的时间复杂度是 O(N^2 * N!)

分析回溯时间复杂度的另一种技巧

上次说过，时间复杂度就是 叶子节点的个数 乘上 根到叶子的路径长度，

对于 46. 全排列 来说，有 n! 个叶子节点，而每条路径的长度是 n ，因此时间复杂度是 O(n*n!)

---

但是！在计算每条路径的长度时，会有节点被重复计算，因此上面的时间复杂度算法并不精确（比如根节点，在计算每次路径长度时都被参与了运算）。

Q：如何直接计算这棵树有多少个节点？（精确，知道了节点的个数，也就知道了递归的次数）

每一层的节点分别是从 n 个数中选 k 个数的排列，
因此 节点个数：最后为 e * n!

---

但是！ 在 大O 下的时间复杂度其实不需要那么精确，
因此 力扣官方题解下的时间复杂度是这样的：

（是用放缩来做的）