第四章 机器学习

第四章 决策树

4.1基本流程

决策过程：

基本算法：

4.2划分选择

4.2.1信息增益

“信息嫡”(information entropy)是度量样本集合纯度最常用的一种指标.假定当前样本集合D中第k类样本所占的比例为$p_k(k=1,2,\dots ,|\mathcal{Y}|)$，则D的信息嫡定义为 $$\text{Ent}(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k$$Ent(D)的值越小，则D的纯度越高.

假定离散属性$a$有$V$个可能的取值$\{a^1,a^2,...,a^V\}$,若使用a来对样本集D进行划分,则会产生$V$个分支结点,其中第$v$个分支结点包含了$D$中所有在属性$a$上取值为$a^v$的样本,记为$D^v$．我们可根据上式计算出$D^v$的信息嫡,再考虑到不同的分支结点所包含的样本数不同,给分支结点赋予权重$|D^v|/|D|$,即样本数越多的分支结点的影响越大,于是可计算出用属性$a$对样本集D进行划分所获得的“信息增益”(information gain)$$\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}\mathrm{Ent}(D^v)$$

例：

8好瓜，9坏瓜：$$\text{Ent}(D)=-\sum _{k=1}^2{p}_k{\log }_2{p}_k=-\left(\frac{8}{17}{\log }_2\frac{8}{17}+\frac{9}{17}{\log }_2\frac{9}{17}\right)=0.998$$
以色泽划分子集：

• $D_1(色泽=青绿):\{1,4,6,10,13,17\},\frac{好瓜}{好瓜+坏瓜}=\frac{3}{6}$
• $D_2(色泽=乌黑):\{2,3,7,8,9,15\},\frac{好瓜}{好瓜+坏瓜}=\frac{3}{6}$
• $D_3(色泽=泽白):\{5,11,12,14,16\},\frac{好瓜}{好瓜+坏瓜}=\frac{1}{5}$

信息熵：$$\begin{array}{ccccc}\text{Ent}(D^1)& =& -\left(\frac{3}{6}{\log }_2\frac{3}{6}+\frac{3}{6}{\log }_2\frac{3}{6}\right)& =& 1.000\\ \text{Ent}(D^2)& =& -\left(\frac{4}{6}{\text{log}}_2\frac{4}{6}+\frac{2}{6}{\text{log}}_2\frac{2}{6}\right)& =& 0.918\\ \text{Ent}(D^3)& =& -\left(\frac{1}{5}{\log }_2\frac{1}{5}+\frac{4}{5}{\log }_2\frac{4}{5}\right)& =& 0.722\end{array}$$
信息增益$\text{Gain}(D,色泽)$： $$\begin{array}{rl}\text{Gain}(D,色泽)& =\text{Ent}(D)-\sum _{v=1}^3\frac{|D^v|}{|D|}\text{Ent}(D^v)\\ & =0.998-\left(\frac{6}{17}\times 1.000+\frac{6}{17}\times 0.918+\frac{5}{17}\times 0.722\right)\\ & =0.109\end{array}$$
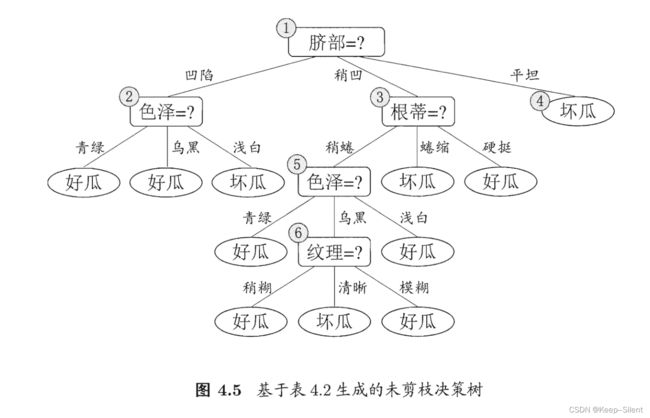
以此算出其他属性后划分决策树如下所示：

4.2.2增益率

增益率：$$\begin{array}{c}Gain\_ratio(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)},\\ \mathrm{IV}(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}{\log }_2\frac{|D^v|}{|D|}\end{array}$$

4.2.3基尼指数

CART决策树使用“基尼指数”(Gini index)来选择划分属性.数据集D的纯度可用基尼值来度量:$$\begin{array}{rl}\mathrm{Gini}(D)& =\sum _{k=1}^{|Y|}\sum _{k^{\prime }\ne k}^{|Y|}{p}_k{p}_{k^{\prime }}\\ & =1-\sum _{k=1}^{|\mathcal{Y}|}{p}_k^2\end{array}$$

直观来说，Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率.因此, Gini(D)越小，则数据集D的纯度越高.
属性a的基尼指数定义为$$\text{Gini\_index}(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}\text{Gini}(D^v)$$
于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性,即$a_{\ast }=\underset{a\in A}{\mathrm{argmin}}\mathrm{Gini}\text{\_index}(D,a)$.

4.3剪枝处理

剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段.基本策略：“预剪枝”和“后剪枝”。

4.3.1预剪枝

划分前，对划分前后的泛化性能进行估计：如果划分后性能不变或者性能下降，则剪枝。如下图所示

4.3.2后剪枝

划分后，对结点进行考察：如果将其领衔的子树替换为叶结点，验证集精度提高，则剪枝。如下图所示

4.4连续与缺失值

4.4.1连续值处理

给定样本集D和连续属性$a$,假定$a$在D上出现了n个不同的取值,将这些值从小到大进行排序,记为$\{a^1,a^2,\dots ,a^n\}$．基于划分点t可将D分为子集$D_t^{-}$和$D_t^{+}$,其中$D_t^{-}$,包含那些在属性$a$上取值不大于t的样本,而$D_t^{-}$则包含那些在属性a上取值大于t的样本．显然,对相邻的属性取值$a^i$与$a^{i+1}$来说, 在区间$[a,a^{i+1})$ 中取任意值所产生的划分结果相同.因此,对连续属性$a$，我们可考察包含$n-1$个元素的候选划分点集合（把中位点作为划分）$$T_a=\left\{\frac{a^i+a^{i+1}}{2}\mid 1⩽i⩽n-1\right\}$$ 划分点为：$$\begin{array}{rl}\text{Gain}(D,a)=& \underset{t\in T_a}{\max }\text{Gain}(D,a,t)\\ =& \underset{t\in T_a}{\max }\text{Ent}(D)-\sum _{\lambda \in \{-,+\}}\frac{|D_t^{\lambda }|}{|D|}\text{Ent}(D_t^{\lambda })\end{array}$$

4.4.2缺失值处理

我们需解决两个问题:

1. 如何在属性值缺失的情况下进行划分属性选择？

取没有缺失值的样本子集去计算后选取

2. 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?

同一个样本以不同的概率划分到不同的子节点去

为每个样本$x$赋予权重$w_x$:$$\begin{array}{c}\rho =\frac{{\sum }_{x\in \tilde{D}}{w}_x}{{\sum }_{x\in D}{w}_x}\\ p_k=\frac{{\sum }_{x\in {\tilde{D}}_k}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}\\ r_v=\frac{{\sum }_{x\in {\tilde{D}}^v}{w}_x}{{\sum }_{x\in \tilde{D}}{w}_x}\end{array}$$
信息增益为：$$\begin{gathered} \begin{array}{rl}\text{Gain}(D,a)& =\rho \times \text{Gain}(\tilde{D},a)\\ & =\rho \times \left(\text{Ent}\left(\tilde{D}\right)-\sum _{v=1}^V{\tilde{r}}_v\text{Ent}\left({\tilde{D}}^v\right)\right)\end{array} \\ \text{Ent}(\tilde{D})=-\sum _{k=1}^{|Y|}{\tilde{p}}_k{\log }_2{\tilde{p}}_k \end{gathered}$$

4.5多变量决策树

学习任务的真实分类边界比较复杂时,必须使用很多段划分才能获得较好的近似。