Apriori算法详解与实现

一、摘要

  本文讲解Apriori算法的原理，梳理了Apriori算法的实现流程，并使用Java实现Apriori算法，通过Java自身集合操作和缓存等操作减少算法的扫描次数，使Apriori算法具有较高的性能。

二、绪论

  随着社会经济和购买力的不断发展，商场也面临着急剧膨胀的购买记录，如何通过研究购买记录来获取购买规律来提高收益也便成为了研究热点。沃尔玛发现，当一个人购买尿布，那么他便有很高的几率购买啤酒，这就是著名的“啤酒与尿布”的故事。研究“啤酒与尿布”关联的方法就是购物篮分析，购物篮分析曾经是沃尔玛秘而不宣的独门武器，购物篮分析可以帮助门店的销售过程中找到具有关联关系的商品，并以此获得销售收益的增长。而Apriori就是用来挖掘数据关联规则最经典的算法。

三、算法介绍

  在介绍算法之前，我们需要先了解几个概念。

1、项目

  项目是数据集中最小的独立单位，比如在购物记录中，“牛奶”便是一个项目。

2、项集

  项集是项目的集合，如一条购物记录便对应着一个项集，就像{“牛奶”，“饼干”，“汽水”}。

3、项集的支持度

  支持度被定义为数据集中包含该项集的记录所占的比例，是针对项集来说的。在算法过程中，我们可以通过设置最小支持度来对关联程度低于阈值的项集进行枝剪。如：在n条购物记录中有m条包含“牛奶”，则“牛奶”的支持度为m/n；又比如在n条购物记录中有k条同时包含“牛奶”和“巧克力”，则项集{“牛奶”，“巧克力”}的支持度为k/n。

4、关联规则

  关联规则X->Y表示在事件X发生的前提下同时发生事件Y。

5、关联规则的置信度

  置信度confidence(X->Y) = P(Y|X) = P(XY)/P(X)，指的是发生Y事件基础上发生事件X的概率（条件概率）。如“牛奶”->“巧克力”的置信度为50%，支持度为5%，则意味着总共有5%的顾客既买了“牛奶”也买了“巧克力”，买“牛奶”的顾客中有50%的人还买了“巧克力”。

6、频繁k项集

  频繁项集就是在数据集中频繁出现的项集。如果一个项集中含有k个项目，则称为k项集，若同时满足最小支持度，则该项集为频繁k项集。

7、算法流程

  了解上述概念后我们便可以开始Apriori算法的流程了。
  首先我们需要求出最终频繁项集，即满足最小支持度的频繁k项集（k尽可能大）。
  频繁项集主要通过迭代计算获取频繁k项集，迭代过程如下：
（1）计算PRE区中k项集的支持度；
（2）通过枝剪过滤掉不满足最小支持度的项集，得到频繁k项集（LATER区）；
（3）通过全连接（或并操作）获取k+1项集；
（4）计算k+1项集的支持度，并将k+1项集移入PRE区，令k=k+1；
（5）重复（1）。
  迭代终止条件为不存在k+1项集时，上次迭代的频繁k项集便是最终项集。
  这里我们给出一个实例，对于数据集

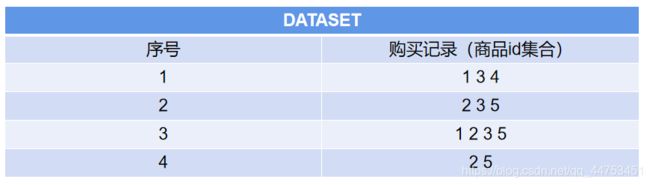
其迭代过程为

在代码中输出每一轮的结果为

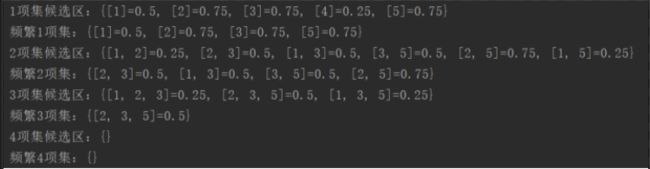
验证了迭代过程的正确性。

  在找到所有频繁项集之后，我们需要根据这些频繁项集来确定关联规则，步骤如下：
（1）遍历所有的最终频繁项集，对于每个频繁项集A：
（2）求出A的所有非空真子集的集合U，对U中任意互补集X和Y，利用公式confidence(X->Y) = P(Y|X) = P(XY)/P(X)求出置信度c，如果c小于设置的最小置信度则舍弃，如果大于则保留。
  这里给出一个详细的例子。对于上面的例子，之前已经求出最终频繁项集，为{2 3 5}，我们对其进行获取关联规则的操作：

  至此，算法流程就结束了。虽然算法中有缓存支持度等优化效率的操作，但在这里不多做解释，在代码中有较详细的注释。

四、代码实现

import java.io.File;
import java.io.FileNotFoundException;
import java.util.*;

public class Apriori {
    // 数据集
    private static ArrayList<ArrayList<String>> DATASET = new ArrayList<>();
    // 待选集区域
    private static HashMap<ArrayList<String>, Double> PRE = new HashMap<>();
    // 频繁集区域
    private static HashMap<ArrayList<String>, Double> LATER = new HashMap<>();
    // 缓存项集支持度
    private static HashMap<ArrayList<String>, Double> CACHE = new HashMap<>();
    // 提前算好加数单元
    private static double ADD_UNIT;
    // 最小支持度
    private static double MIN_SUPPORT = 0.5;
    // 最小置信度
    private static double MIN_CONFIDENT = 0.8;

    /**
     * 加载数据
     *
     * @param filePath 文件路径
     */
    private static void loadData(String filePath) {
        Scanner scanner;
        try {
            scanner = new Scanner(new File(filePath));
            while (scanner.hasNext()) {
                DATASET.add(new ArrayList<>(Arrays.asList(scanner.nextLine().split(" "))));
            }
            scanner.close();
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        }
        // 单元加数
        ADD_UNIT = 1.0 / DATASET.size();
    }

    /**
     * 枝剪，过滤掉小于最小支持度的项集
     */
    private static void pruning() {
        LATER.clear();
        // 先全加过来等待删除不满足最小支持度的项集
        LATER.putAll(PRE);
        // 删除少于最小支持度的元素
        ArrayList<ArrayList<String>> deletedKeys = new ArrayList<>();
        for (ArrayList<String> key : LATER.keySet()) {
            if (LATER.get(key) < MIN_SUPPORT) {
                deletedKeys.add(key);
            }
        }
        for (ArrayList<String> key : deletedKeys) {
            LATER.remove(key);
        }
    }

    /**
     * 加载数据并求得一项集
     */
    private static void init() {
        loadData("E:\\data_mining_lab\\src\\data\\test.txt");

        // 求得一项集的支持度
        for (ArrayList<String> record : DATASET) {
            for (String item : record) {
                String[] itemArr = {item};
                ArrayList<String> itemList = new ArrayList<>(Arrays.asList(itemArr));
                if (!PRE.containsKey(itemList)) {
                    PRE.put(itemList, ADD_UNIT);
                } else {
                    PRE.put(itemList, PRE.get(itemList) + ADD_UNIT);
                }
            }
        }

        // 剪枝
        pruning();

        CACHE.putAll(LATER);

    }

    /**
     * 求并集
     *
     * @param arr1
     * @param arr2
     * @return
     */
    private static ArrayList<String> union(ArrayList<String> arr1, ArrayList<String> arr2) {
        Set<String> set = new HashSet<>(arr1);
        set.addAll(arr2);
        return new ArrayList<>(set);
    }

    /**
     * 迭代求出最终的频繁集
     *
     * @return
     */
    private static void getFrequentItemSet() {
        // 缓存上一次迭代的结果
        HashMap<ArrayList<String>, Double> preFrequentItemSet = new HashMap<>();
        // 迭代次数（等同于项集中项目的数量）
        int epoch = 1;

        printStage(epoch);

        // 当频繁项集数量为0时，上一次迭代的结果便是最终的频繁项集
        while (LATER.size() > 0) {
            epoch++;
            // 缓存上次结果
            preFrequentItemSet.clear();
            preFrequentItemSet.putAll(LATER);
            // 进行全连接
            PRE.clear();
            ArrayList<ArrayList<String>> itemsList = new ArrayList<>(LATER.keySet());
            for (int i = 0; i < itemsList.size(); i++) {
                for (int j = i + 1; j < itemsList.size(); j++) {
                    // 求并集
                    ArrayList<String> unionItem = new ArrayList<>(union(itemsList.get(i), itemsList.get(j)));
                    //
                    if (unionItem.size() == epoch) {
                        PRE.put(unionItem, 0.0);
                    }
                }
            }
            // 求支持度
            for (ArrayList<String> key : PRE.keySet()) {
                for (ArrayList<String> record : DATASET) {
                    if (record.containsAll(key)) {
                        PRE.put(key, PRE.get(key) + ADD_UNIT);
                    }
                }
            }
            // 枝剪
            pruning();
            // 缓存
            CACHE.putAll(LATER);

            printStage(epoch);
        }

        LATER = preFrequentItemSet;
    }

    /**
     * 打印候选集和频繁项集
     *
     * @param epoch ： 迭代次数
     */
    private static void printStage(int epoch) {
        System.out.println(epoch + "项集候选区：" + PRE);
        System.out.println("频繁" + epoch + "项集：" + LATER);
    }

    /**
     * 求子集
     *
     * @param parent
     * @return
     */
    private static ArrayList<ArrayList<String>> getSubset(ArrayList<String> parent) {
        if (parent.size() > 0) {
            ArrayList<ArrayList<String>> result = new ArrayList<>();
            // 子集个数为 2^n
            for (int i = 0; i < Math.pow(2, parent.size()); i++) {
                ArrayList<String> subSet = new ArrayList<>();
                int index = i;
                for (String s : parent) {
                    if ((index & 1) == 1) {
                        subSet.add(s);
                    }
                    index >>= 1;
                }
                result.add(subSet);
            }
            return result;
        } else {
            throw new NoSubsetException();
        }
    }

    /**
     * 相交是否为空
     *
     * @param arr1
     * @param arr2
     * @return
     */
    private static boolean isIntersectionNull(ArrayList<String> arr1,
                                              ArrayList<String> arr2) {
        Set<String> s1 = new HashSet<>(arr1);
        Set<String> s2 = new HashSet<>(arr2);

        s1.retainAll(s2);

        return s1.size() <= 0;
    }

    /**
     * 根据最终的关联集，根据求出关联规则
     */
    private static void getConnections() {
        // 遍历所有的最终频繁项集
        for (ArrayList<String> key : LATER.keySet()) {
            ArrayList<ArrayList<String>> subsets = getSubset(key);
            for (ArrayList<String> items1 : subsets) {
                // 非空真子集
                if (items1.size() > 0 && items1.size() < key.size()) {
                    double itemsSupport1 = getCache(items1);
                    // 第二个非空真子集
                    for (ArrayList<String> items2 : subsets) {
                        // 两个真子集需要互补
                        if (items2.size() > 0 && items2.size() < key.size() && union(items1, items2).equals(key) && isIntersectionNull(items1, items2)) {
                            // 事件的置信度
                            double confident = getCache(union(items1, items2)) / itemsSupport1;
                            //System.out.println(getCache(union(items1, items2)) + " " + itemsSupport1);
                            //System.out.println("互补子集" + items1 + "->" + items2 + " 置信度：" + confident);
                            // 如果事件的置信度大于最小置信度
                            if (confident > MIN_CONFIDENT) {
                                // 关联规则
                                System.out.println(items1 + "->" + items2 + " 置信度：" + confident);
                            }
                        }
                    }
                }
            }
        }
    }

    /**
     * 从缓存中获取支持度
     *
     * @param items : 目标项集
     * @return
     */
    private static double getCache(ArrayList<String> items) {
        // 尝试从缓存中获取
        Double suppose = CACHE.get(items);
        // 如果缓存中没有，则计算支持度并缓存
        if (suppose == null) {
            CACHE.put(items, 0.0);
            for (ArrayList<String> record : DATASET) {
                if (record.containsAll(items)) {
                    CACHE.put(items, CACHE.get(items) + ADD_UNIT);
                }
            }

            suppose = CACHE.get(items);
        }

        return suppose;
    }

    public static void main(String[] args) {
        // 初始化程序
        init();
        // 求得频繁项集
        getFrequentItemSet();
        // 获取关联规则
        getConnections();
    }

    static class NoSubsetException extends RuntimeException {
        NoSubsetException() {
            super("无子集");
        }
    }
}

五、引用

Apriori算法是什么？适用于什么情境？
【Java】Apriori算法