1. Pearson积差相关。
积差相关也称积矩相关,是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法,因而又称为皮尔逊相关。其计算公式为
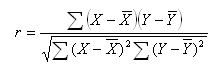
若|r|越接近于0,则表明x与y之间呈直线关系的密切程度较低;若|r|越接近于1,则表明x与y之间呈直线关系的密切程度越高。
积差相关适应于
(1)两个变量之间是线性关系,都是连续数据。
(2)两个变量的总体是正态分布,或接近正态的单峰分布。
(3)两个变量的观测值是成对的,每对观测值之间相互独立。
2. Spearman等级相关
斯皮尔曼等级相关对数据条件的要求没有积差相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关来进行研究。
计算等级相关系数可以将数据变换成等级以后用Pearson相关系数公式计算,也可以计算出每一对样本的等级之差d,然后计算
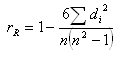
其中n表示样本容量,即数据的对数。
3. Kendall等级相关系数。
适应于两个分类变量均为有序分类的情况,对相关的有序变量进行非参数相关检验。相关系数定义如下
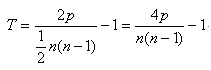
其中n为样本容量,p表示在所有的项中,排在本项之后的项数之和。
例如,有某人A在8人组中,身高排第1,体重排第3。数据形式如下。
Person
|
A |
B |
C |
D |
E |
F |
G |
H |
| Rank by Height |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Rank by Weight |
3 |
4 |
1 |
2 |
5 |
7 |
8 |
6 |
 注意到A的体重排3,在它右边有4,1,2,5,7,8,6.那么排序在它右边的有4,5,7,8,6.这样的话,排序在它右边的有5个数。同理,对B,排序在它右边的数有4个。所有这些项的和加起来,即p=5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.最终,T=88/56-1=0.57.附SAS代码。
注意到A的体重排3,在它右边有4,1,2,5,7,8,6.那么排序在它右边的有4,5,7,8,6.这样的话,排序在它右边的有5个数。同理,对B,排序在它右边的数有4个。所有这些项的和加起来,即p=5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.最终,T=88/56-1=0.57.附SAS代码。

 Code
Code
proc contents data=InData /*Dataset*/
out=InVar(keep=varnum name)
noprint;
run;
proc sql noprint;
select distinct name
into :VarName separated by ' '
from InVar
order by varnum;
run;
%put &VarName;
ods listing close;
ods output spearmancorr=spearman
hoeffdingcorr=hoeffding;
proc Corr data=InData spearman hoeffding rank;
var &VarName;
with Flg;
run;
ods listing;
data spearman1(keep=variable scorr spvalue ranksp);
length variable $ 16;
set spearman;
array best(6) best1--best6;/*6 is number of variable*/
array r(6) r1--r6;
array p(6) p1--p6;
do i=1 to 6;
variable=best(i);
scorr=r(i);
spvalue=p(i);
ranksp=i;
output;
end;
run;
data hoeffding1(keep=variable hcorr hpvalue rankho);
length variable $ 16;
set hoeffding;
array best(6) best1--best6;;/*6 is number of variable*/
array r(6) r1--r6;
array p(6) p1--p6;
do i=1 to 6;
variable=best(i);
hcorr=r(i);
hpvalue=p(i);
rankho=i;
output;
end;
run;
proc sort data=spearman1;
by variable;
run;
proc sort data=hoeffding1;
by variable;
run;
data correlations;
merge spearman1 hoeffding1;
by variable;
run;
proc sort data=correlations;
by ranksp;
run;
proc print data=correlations label split='*';
var variable ranksp rankho scorr spvalue hcorr hpvalue;
label ranksp='Spearman rank*of variable'
scorr='Spearman Correlation'
spvalue='Spearman p-value'
rankho='Hoeffding rank*of variable'
hcorr='Hoeffding Correlation'
hpvalue='Hoeffding p-value';
run;
proc contents data=InData(drop=Flg ID_CLIENT ID_Shop Sex Marital_Status Flg_Phone Area_Code_Phone Payment_Day Shop_Rank
Residence_Type Flg_M Flg_F Flg_Rw Flg_SW Jobcode Flg_RP)
out=InVar(keep=varnum name)
noprint;
run;
proc sql noprint;
select distinct name
into :VarName separated by ' '
from InVar
order by varnum;
run;
%put &VarName;
ods listing close;
ods output spearmancorr=spearman
hoeffdingcorr=hoeffding;
proc Corr data=InData spearman hoeffding rank;
var &VarName;
with Flg;
run;
ods listing;
data spearman1(keep=variable scorr spvalue ranksp);
length variable $ 16;
set spearman;
array best(6) best1--best6;
array r(6) r1--r6;
array p(6) p1--p6;
do i=1 to 6;
variable=best(i);
scorr=r(i);
spvalue=p(i);
ranksp=i;
output;
end;
run;
data hoeffding1(keep=variable hcorr hpvalue rankho);
length variable $ 16;
set hoeffding;
array best(6) best1--best6;
array r(6) r1--r6;
array p(6) p1--p6;
do i=1 to 6;
variable=best(i);
hcorr=r(i);
hpvalue=p(i);
rankho=i;
output;
end;
run;
proc sort data=spearman1;
by variable;
run;
proc sort data=hoeffding1;
by variable;
run;
data correlations;
merge spearman1 hoeffding1;
by variable;
run;
proc sort data=correlations;
by ranksp;
run;
proc print data=correlations label split='*';
var variable ranksp rankho scorr spvalue hcorr hpvalue;
label ranksp='Spearman rank*of variable'
scorr='Spearman Correlation'
spvalue='Spearman p-value'
rankho='Hoeffding rank*of variable'
hcorr='Hoeffding Correlation'
hpvalue='Hoeffding p-value';
run;
 Code
Code
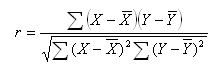
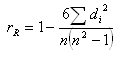
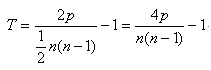
 注意到A的体重排3,在它右边有4,1,2,5,7,8,6.那么排序在它右边的有4,5,7,8,6.这样的话,排序在它右边的有5个数。同理,对B,排序在它右边的数有4个。所有这些项的和加起来,即p=5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.最终,T=88/56-1=0.57.附SAS代码。
注意到A的体重排3,在它右边有4,1,2,5,7,8,6.那么排序在它右边的有4,5,7,8,6.这样的话,排序在它右边的有5个数。同理,对B,排序在它右边的数有4个。所有这些项的和加起来,即p=5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.最终,T=88/56-1=0.57.附SAS代码。