基础算法-前缀和&差分

前缀和

顾名思义，前缀和表示求当前前缀之和，一般应用于求一段区间的数之和。
假设我们存数的数组为a[],前缀和数组为sum[]，那么sum[i]=sum[i-1]+a[i]，表示本位的前缀和为前一位的前缀和加上本位的值。
那么求一段区间[l,r]之和便可以表示为sum[r]-sum[l-1],是一个非常好的预处理方法。

例题一：前缀和

输入一个长度为 n 的整数序列。
接下来再输入 m 个询问，每个询问输入一对 l,r。
对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式

第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数数列。
接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式

共 m 行，每行输出一个询问的结果。

前缀和模板：

#include "bits/stdc++.h"
using namespace std;
const int N = 100010;
int a[N],sum[N],n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
    while (m -- ){
        int l,r;
        cin>>l>>r;
        cout<<sum[r]-sum[l-1]<<endl;
    }
}

二维前缀和

前缀和是简单的在一个一维数组上进行前缀求和，那二维前缀和顾名思义便是在二维数组上进行前缀求和。
那么对于二维数组中的点(i,j)来说，它的前缀便是行(1~i) 列(1~j)所组成的方形。
那二维数组前缀和可表示为sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]
当前这个点再加上前一行的前缀和，再加上前一列的前缀和，再减去重复加的部分。

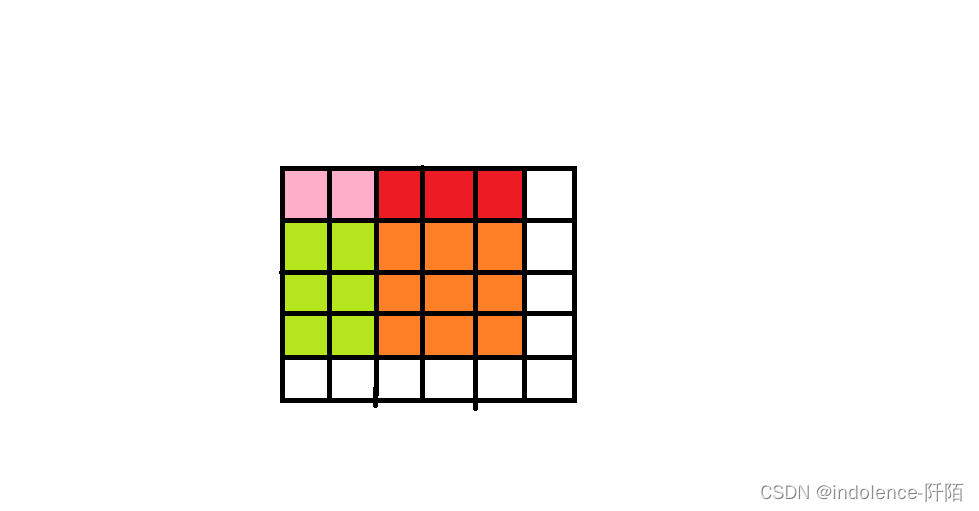
如图，我们在求解二维数组从点l1,r1到点l2,r2之间数之和时，便可以表示为
res=sum[l2][r2]-sum[l1-1][r2]-sum[l2][r1-1]+sum[l1-1][r1-1]

例题二：Counting Rectangles(codeforces 1722E)

You have n rectangles, the i-th rectangle has height hi and width wi.

You are asked q queries of the form hs ws hb wb.

For each query output, the total area of rectangles you own that can fit a rectangle of height hs and width ws while also fitting in a rectangle of height hb and width wb. In other words, print ∑hi⋅wi for i such that hs

Please note, that if two rectangles have the same height or the same width, then they cannot fit inside each other. Also note that you cannot rotate rectangles.

题目大意：

第一行给我们n，q。
给我们n个点(h,w),每个点的权值为h*w。
再给出q个询问，每个询问给出hs,ws,hb,wb.
问在(hs,hb),(ws,wb)间的点的权值之和是多少。

输入格式

第一行包含一个整数 t，表示样例个数。
第二行包含 2个整数，n,q。
接下来 n 行，每行包含两个整数 h 和 w，表示一个点的位置。
接下来 q 行，每行包含四个整数 hs,ws,hb,wb。

输出格式

共 m 行，每行输出一个询问的结果。

二维前缀和模板：

#include "bits/stdc++.h"
#define int long long
#define mod 1000000007
using namespace std;
const int N=100010;
int t,n,res,q,m[1010][1010],ans[1010][1010];
inline int read()//快读
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9')f=(ch=='-'?-1:1),ch=getchar();
	while(ch>='0'&& ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x*f;
}
inline void write(int x) //快写
{
     if(x<0) putchar('-'),x=-x;
     if(x>9) write(x/10);
     putchar(x%10+'0');
}
signed main()
{
    //ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    t=read();
    while(t--)
    {
        memset(m,0,sizeof m);
        memset(ans,0,sizeof ans);
        n=read();q=read();
        while(n--)
        {
            int j,k;
            cin>>j>>k;
            m[j][k]+=j*k;
        }
        for(int i=1;i<=1000;i++)
            for(int j=1;j<=1000;j++)
            {
                ans[i][j]=m[i][j]+ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
            }
        while(q--)
        {
            int l,r,ll,rr;
            l=read();r=read();ll=read();rr=read();
            cout<<ans[ll-1][rr-1]-ans[ll-1][r]-ans[l][rr-1]+ans[l][r]<<endl;
        }
    }
}

前缀和可以理解成对前缀有影响
差分可以理解成对后缀有影响

差分

差分表示的是当前数与前一个数之差，一般用于求解一段区间加/减上一个数。
差分可以看作是前缀和的逆向，如果做一遍差分再做一遍前缀和的话便会回到原来的样子。
假设我们存数的数组为a[],差分数组为sub[]，那么sub[i]=a[i]-a[i-1]。表示本位与前一位的差分值。
那么对一段区间l，r加上一个数x，便可以表示为sub[l]+=x;sub[r+1]-=x;。
那么怎么理解呢，由于我们是先差分后做前缀和来完成一段区间的加减，那么sub[l]+=x在后面做前缀和的时候便是从l到末尾都加上了x，由于我们只需要[l,r]加x，故sub[r+1]-=x;

例题三： 差分

输入一个长度为 n 的整数序列。
接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。
第二行包含 n 个整数，表示整数序列。
接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式

共一行，包含 n 个整数，表示最终序列。

差分模板：

#include "bits/stdc++.h"
using namespace std;
const int N = 100010;
int n,m,a[N],sub[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) sub[i]=a[i]-a[i-1];
    while (m -- ){
        int l,r,x;
        cin>>l>>r>>x;
        sub[l]+=x;
        sub[r+1]-=x;
    }
    for(int i=1;i<=n;i++) 
    {
        sub[i]+=sub[i-1];
        cout<<sub[i]<<' ';
    }
}

二维差分

二维差分顾名思义便是差分在二维数组上的实现，差分我们可以理解成对后缀有影响，那么二维矩阵的后缀是什么呢。
对于二维数组上的点(i,j)来说，它的后缀便是行[i,n]列[j,m]组成的方形。
二维差分数组的构造表示为：sub[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]
那如何表示在一个子矩阵上的加减呢，如下图：

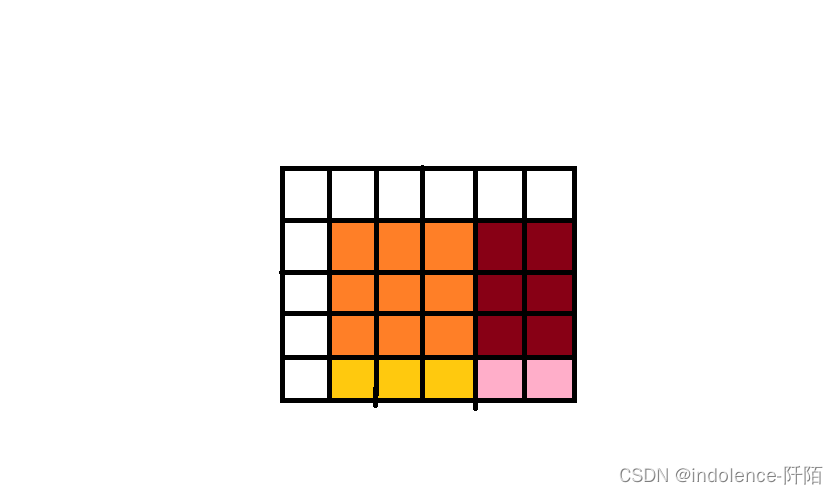
如果我们要在橙色子矩阵上进行加减，那么我们表示为：
sub[l1][r1]+=x;sub[l1][r2+1]-=x;sub[l2+1][r1]-=x;sub[l2+1][r2+1]+=x;
左上角加上x，再减去多的部分，再加回重复减的部分。

例题四： 差分矩阵

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。
接下来 n 行，每行包含 m 个整数，表示整数矩阵。
接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

二维差分模板：

#include "bits/stdc++.h"
using namespace std;
const int N = 1010;
int a[N][N],sub[N][N],n,m,q;
int main()
{
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++) 
        for(int j=1;j<=m;j++) 
        {
            cin>>a[i][j];
            sub[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
        }
    while(q--){
        int l1,r1,l2,r2,x;
        cin>>l1>>r1>>l2>>r2>>x;
        sub[l1][r1]+=x;
        sub[l1][r2+1]-=x;
        sub[l2+1][r1]-=x;
        sub[l2+1][r2+1]+=x;
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            sub[i][j]=sub[i][j]+sub[i-1][j]+sub[i][j-1]-sub[i-1][j-1];
            cout<<sub[i][j]<<' ';
        }
        cout<<endl;
    }
}