【离群点检测算法】离群点|异常值 检测算法——局部离群因子LOF算法
every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
离群点检测，理解起来也比较容易。
同学都考70分，你也考70分，可以。
同学都考90分，你考70分，不可以。
1. 正文
Local Outlier Factor（LOF）是基于密度的经典算法
论文：https://www.dbs.ifi.lmu.de/Publikationen/Papers/LOF.pdf
1.1 概述
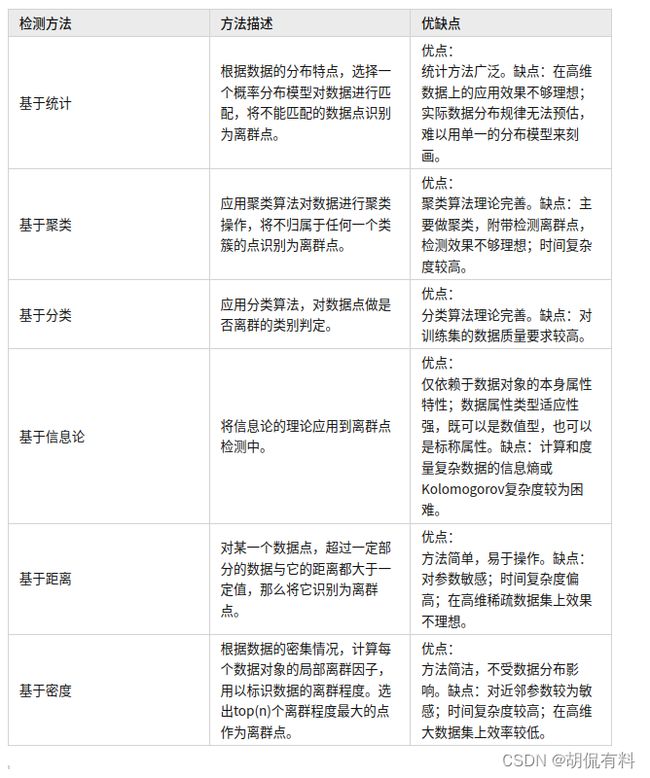
关于离群点 检测的方法还是比较多，主要有基于统计、聚类、分类、信息论、距离、密度等。
1.2 相关应用
应用比较广泛，有以下：
- 欺诈检测：信用卡、电话卡欺诈使用
- 工业检测：计算机网络的非法入侵
- 活动监控：实时手机活跃度，实现检测移动手机诈骗行为
- 网络性能：计算机网络性能检测
- 生态监测：生态系统失调、异常自然气候等的发现
- 公共服务：公共卫生中的异常疾病爆发。
1.3 初步理解
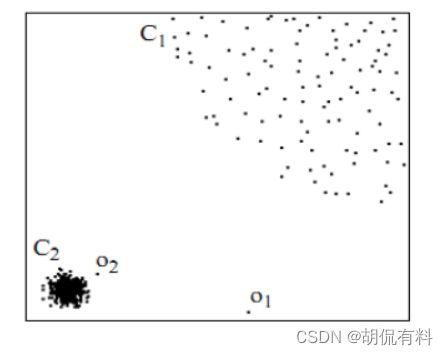
C1、C2形成了两簇，而o1、o2是两个离群点，我们任务就需要找出他们。
如果基于距离，o2到最近的C1的距离肯可能小于C1内部元素的距离，从而无法正确检测出。如果基于全局密度，很可能出现相同的情况。
所以正确的做法是基于局部密度，这是我们的直观感受，具体怎么做，且看下文。
1.4 基础概念
(1). 两点距离
d(p,o): 表示P和O两点之间的距离
(2). 第k距离
k-distance
距离点p，（按从近到远）第k近的点和p之间的距离，称为点p的k-邻近距离，记为k-distance§。
(3). 第k距离邻域
k-distance neighborhood of p
点p的第k距离邻域 N k ( p ) N_k(p) Nk(p) ，就是的 第k距离以内的所有点，包括第k距离。
因此，p的第k邻域点的个数 ∣ N k ( p ) ∣ ≥ k |N_k(p)| \geq k ∣Nk(p)∣≥k （存在距离p相同距离的点，所以是大于）
(4). 可达距离
reach-distance
注意： 这里需要理解以下。
点o到点p的第k可达距离定义为：
r e a c h − d i s t a n c e k ( p , o ) = m a x ( k − d i s t a n c e ( o ) , d ( p , o ) ) reach-distance_k(p,o) = max( k-distance(o), d(p,o) ) reach−distancek(p,o)=max(k−distance(o),d(p,o))
这里是两个距离选一个最大，和之前在聚类算法中介绍的有点不一样，主要是因为这里多了**“第k”**。
其实也比较好理解：
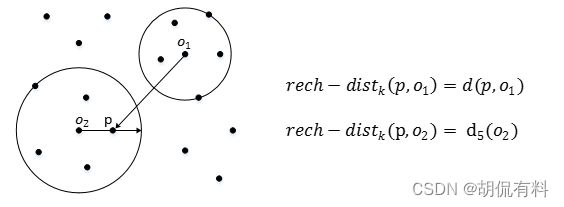
- 如果p点在o点 第k距离外，那么可达距离就是直接距离，d(p,o)
- 如果p点在o点第k距离以内，那么可达距离就是第k距离， d 5 ( o ) d_5(o) d5(o)
如下图所示：
- p相对o1在第k距离外，所以可达距离是直接距离
- p相对o2在第k距离内，所以可达距离是第k距离
(5). 局部可达密度
local reachability density
密度表示为距离倒数，距离越小，密度越大，反之。
故，点p的局部可达密度表示为：
l r d k ( p ) = 1 / ( ∑ o ∈ N k ( p ) r e a c k − d i s t k ( p , o ) ∣ N k ( p ) ∣ ) lrd_k(p) = 1 / ( { \sum_{o \in N_k(p)} reack-dist_k(p,o) \over |N_k(p)| }) lrdk(p)=1/(∣Nk(p)∣∑o∈Nk(p)reack−distk(p,o))
局部可达密度：平均距离的倒数，平均距离为领域内距离和除以邻域内点数
注意： 由于我们的可达距离是非对称的（你离我最近，但我却不是离你最近的点），所以 可达密度也是非对称的。
(6). 局部离群因子
local reachability density
有了一个点的局部可达密度，怎么确定这个点是不是离群点呢，很简单，只要和周围点的的可达密度进行比较就可以。
表示为：
L O F k ( p ) = ∑ o ∈ N k ( p ) l r d k ( o ) ∣ N k ( p ) ∣ / l r d k ( p ) LOF_k(p) = { \sum_{o \in N_k(p)} { lrd_k(o) } \over |N_k(p)|} / lrd_k(p) LOFk(p)=∣Nk(p)∣∑o∈Nk(p)lrdk(o)/lrdk(p)
表示：p点领域内点 N k ( p ) N_k(p) Nk(p)的局部可达密度 平均值与p点的可达密度之比。
简单说：周围人考70分，你也考70分，ok；周围人考90分，你考70，不ok。
- 比值接近1，说明p和其邻域点密度差不多，可能和邻域属于同一簇
- 比值小于1，p的密度高于邻域点密度，p为密度点
- 比值小于1，p的密度小于其邻域点密度，p可能是异常点
1.5 算法流程
- 计算每个点的lof得分
- lof越大，说明越异常，反之。
1.6 优缺点
A. 优点
- 思想简单。算法简单易于实现
- 利用局部，相比全局更加合理
B. 缺点
- LOF算法中关于局部可达密度的定义其实暗含了一个假设：不存在大于等于 k 个重复的点。如果存在大于k个重复点，那么他们之间的距离为0，密度就会变成无穷大。所以一般会给距离加一个微小值。
- 因为需要计算距离，运算开销大，不适合高维、大数据 。
参考
[1] https://www.cnblogs.com/wj-1314/p/14049195.html
[2] https://blog.csdn.net/wangyibo0201/article/details/51705966
[3] https://zhuanlan.zhihu.com/p/607616813
[4] https://zhuanlan.zhihu.com/p/28178476
[5] https://zhuanlan.zhihu.com/p/37753692
[6] https://zhuanlan.zhihu.com/p/385238291