Real-Time Rendering——5.4 Aliasing and Antialiasing 锯齿和抗锯齿 5.4.1 Sampling and Filtering Theory采样和过滤理论

Imagine a large black triangle moving slowly across a white background. As a screen grid cell is covered by the triangle, the pixel value representing this cell should smoothly drop in intensity. What typically happens in basic renderers of all sorts is that the moment the grid cell’s center is covered, the pixel color immediately goes from white to black. Standard GPU rendering is no exception. See the leftmost column of Figure 5.14.

想象一个巨大的黑色三角形在白色背景上缓慢移动。当屏幕网格单元被三角形覆盖时，代表该单元的像素值的亮度应该平滑下降。在各种基本渲染器中通常会发生的情况是，当网格单元的中心被覆盖时，像素颜色会立即从白色变为黑色。标准GPU渲染也不例外。见图5.14最左边一栏。

Figure 5.14. The upper row shows three images with different levels of antialiasing of a triangle,a line, and some points. The lower row images are magnifications of the upper row. The leftmost column uses only one sample per pixel, which means that no antialiasing is used. The middle column images were rendered with four samples per pixel (in a grid pattern), and the right column used eight samples per pixel (in a 4 × 4 checkerboard, half the squares sampled). 

图5.14。上面一行显示了具有不同抗锯齿级别的三角形、直线和一些点的三个图像。下面一行图像是上面一行的放大图像。最左边的列每像素仅使用一个样本，这意味着没有使用抗锯齿。中间的列图像以每像素四个样本的方式呈现(在网格模式中)，而右边的列使用每像素八个样本的方式呈现(在4 × 4的棋盘中，一半的正方形被采样)。

Triangles show up in pixels as either there or not there. Lines drawn have a similar problem. The edges have a jagged look because of this, and so this visual artifact is called “the jaggies,” which turn into “the crawlies” when animated. More formally,this problem is called aliasing, and efforts to avoid it are called antialiasing techniques.

三角形以像素显示，要么在那里，要么不在那里。画出来的线也有类似的问题。因此，边缘看起来呈锯齿状，因此这种视觉假象被称为“锯齿”，动画制作时会变成“爬虫”。更正式地说，这个问题被称为锯齿，避免它的努力被称为抗锯齿技术。

The subject of sampling theory and digital filtering is large enough to fill its own book. As this is a key area of rendering, the basic theory of sampling and filtering will be presented. We will then focus on what currently can be done in real time to alleviate aliasing artifacts.采样理论和数字滤波的主题足够大，可以写满一本书。由于这是渲染的一个关键领域，采样和过滤的基本理论将被提出。然后，我们将关注当前可以实时做些什么来减轻锯齿伪像。

5.4.1 Sampling and Filtering Theory 采样和滤波理论

The process of rendering images is inherently a sampling task. This is so since the generation of an image is the process of sampling a three-dimensional scene in order to obtain color values for each pixel in the image (an array of discrete pixels). To use texture mapping (Chapter 6), texels have to be resampled to get good results under varying conditions. To generate a sequence of images in an animation, the animation is often sampled at uniform time intervals.This section is an introduction to the topic of sampling, reconstruction, and filtering. For simplicity, most material will be presented in one dimension. These concepts extend naturally to two dimensions as well, and can thus be used when handling two-dimensional images.

渲染图像的过程本质上是一个采样任务。这是因为图像的生成是对三维场景进行采样以获得图像中每个像素(离散像素阵列)的颜色值的过程。要使用纹理映射(第6章)，纹理元素必须重新采样，以在不同的条件下获得良好的结果。为了在动画中生成图像序列，通常以均匀的时间间隔对动画进行采样。本节介绍采样、重构和滤波主题。为简单起见，大部分材料将以一维形式呈现。这些概念自然也扩展到二维，因此可以在处理二维图像时使用。

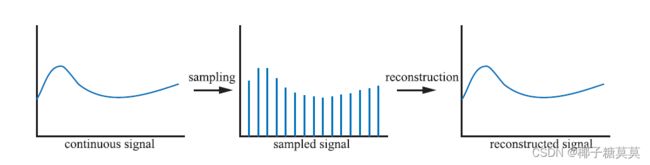
Figure 5.15 shows how a continuous signal is being sampled at uniformly spaced intervals, that is, discretized. The goal of this sampling process is

图5.15显示了一个连续信号是如何以均匀的间隔进行采样的，即离散化。这个取样过程的目标是

 Figure 5.15. A continuous signal (left) is sampled (middle), and then the original signal is recovered by reconstruction (right).

图5.15。对连续信号(左)进行采样(中)，然后通过重构恢复原始信号(右)。

to represent information digitally. In doing so, the amount of information is reduced.However, the sampled signal needs to be reconstructed to recover the original signal. This is done by filtering the sampled signal.

用数字来表示信息。这样做，信息量就减少了。然而，需要重构采样信号以恢复原始信号。这通过对采样信号进行滤波来实现。

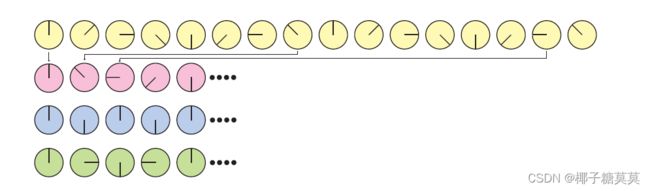
Whenever sampling is done, aliasing may occur. This is an unwanted artifact, and we need to battle aliasing to generate pleasing images. A classic example of aliasing seen in old Westerns is a spinning wagon wheel filmed by a movie camera. Because the spokes move much faster than the camera records images, the wheel may appear to be spinning slowly (backward or forward), or may even look like it is not rotating at all. This can be seen in Figure 5.16. The effect occurs because the images of the wheel are taken in a series of time steps, and is called temporal aliasing.

每当采样完成时，可能会出现锯齿。这是一个不想要的现象，我们需要与锯齿作斗争来生成令人满意的图像。在old Westerns里看到的一个典型的锯齿例子是由电影摄影机拍摄的一个旋转的马车轮子。因为辐条移动的速度比相机记录图像的速度快得多，所以轮子可能看起来旋转得很慢(向后或向前)，或者甚至看起来根本不旋转。这可以从图5.16中看出。出现这种效应是因为车轮的图像是在一系列时间步骤中拍摄的，这被称为时间锯齿。

 Figure 5.16. The top row shows a spinning wheel (original signal). This is inadequately sampled in second row, making it appear to move in the opposite direction. This is an example of aliasing due to a too low sampling rate. In the third row, the sampling rate is exactly two samples per revolution,and we cannot determine in which direction the wheel is spinning. This is the Nyquist limit. In the fourth row, the sampling rate is higher than two samples per revolution, and we suddenly can see that the wheel spins in the right direction.

图5.16。最上面一行显示一个纺车(原始信号)。这在第二行中采样不充分，使其看起来向相反方向移动。这是采样速率过低导致锯齿的一个例子。在第三行中，采样速率正好是每转两个样本，我们无法确定车轮旋转的方向。这是奈奎斯特极限。在第四行中，采样率高于每转两个样本，我们突然可以看到车轮以正确的方向旋转。

Common examples of aliasing in computer graphics are the “jaggies” of a rasterized line or triangle edge, flickering highlights known as “fireflies”, and when a texture with a checker pattern is minified (Section 6.2.2).

计算机图形中锯齿的常见例子是光栅化线或三角形边缘的“锯齿”、被称为“萤火虫”的闪烁高光，以及当具有棋盘图案的纹理被缩小时(6.2.2节)。

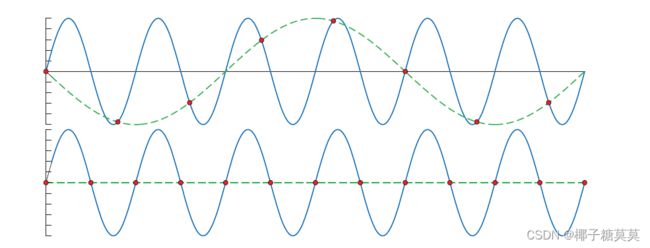
Aliasing occurs when a signal is being sampled at too low a frequency. The sampled signal then appears to be a signal of lower frequency than the original. This is illustrated in Figure 5.17. For a signal to be sampled properly (i.e., so that it is possible to reconstruct the original signal from the samples), the sampling frequency has to be more than twice the maximum frequency of the signal to be sampled. This is often called the sampling theorem, and the sampling frequency is called the Nyquist rate [1447] or Nyquist limit, after Harry Nyquist (1889–1976), a Swedish scientist who discovered this in 1928. The Nyquist limit is also illustrated in Figure 5.16. The fact that the theorem uses the term “maximum frequency” implies that the signal has to be band-limited, which just means that there are not any frequencies above a certain limit. Put another way, the signal has to be smooth enough relative to the spacing between neighboring samples.

当信号采样频率过低时，就会出现锯齿现象。采样信号看起来比原始信号的频率低。这如图5.17所示。对于要被正确采样的信号(即，使得可以从样本中重构原始信号)，采样频率必须大于要被采样的信号的最大频率的两倍。这通常被称为采样定理，采样频率被称为奈奎斯特速率[1447]或奈奎斯特极限，以瑞典科学家哈利·奈奎斯特(1889-1976)的名字命名，他于1928年发现了这一现象。奈奎斯特极限也如图5.16所示。该定理使用术语“最大频率”的事实意味着信号必须是带限的，这仅仅意味着没有任何频率高于某一极限。换句话说，相对于相邻样本之间的间隔，信号必须足够平滑。

Figure 5.17. The solid blue line is the original signal, the red circles indicate uniformly spaced sample points, and the green dashed line is the reconstructed signal. The top figure shows a too low sample rate. Therefore, the reconstructed signal appears to be of lower frequency, i.e., an alias of the original signal. The bottom shows a sampling rate of exactly twice the frequency of the original signal, and the reconstructed signal is here a horizontal line. It can be proven that if the sampling rate is increased ever so slightly, perfect reconstruction is possible. 

图5.17。蓝色实线是原始信号，红色圆圈表示均匀间隔的样本点，绿色虚线是重构信号。上图显示了过低的采样速率。因此，重建的信号看起来具有较低的频率，即原始信号的锯齿。底部显示的采样率正好是原始信号频率的两倍，这里重建的信号是一条水平线。可以证明，如果采样率稍微增加一点，完美的重建是可能的。

A three-dimensional scene is normally never band-limited when rendered with point samples. Edges of triangles, shadow boundaries, and other phenomena produce a signal that changes discontinuously and so produces frequencies that are infinite [252].Also, no matter how closely packed the samples are, objects can still be small enough that they do not get sampled at all. Thus, it is impossible to entirely avoid aliasing problems when using point samples to render a scene, and we almost always use point sampling. However, at times it is possible to know when a signal is band-limited.One example is when a texture is applied to a surface. It is possible to compute the frequency of the texture samples compared to the sampling rate of the pixel. If this frequency is lower than the Nyquist limit, then no special action is needed to properly sample the texture. If the frequency is too high, then a variety of algorithms are used to band-limit the texture (Section 6.2.2).

使用点采样渲染时，三维场景通常不会受到带宽限制。三角形的边缘、阴影边界和其他现象会产生不连续变化的信号，从而产生无限的频率[252]。此外，无论样本多么密集，对象仍然可能小到根本无法采样。因此，当使用点采样渲染场景时，不可能完全避免走样问题，我们几乎总是使用点采样。然而，有时可以知道信号何时是带限的。一个例子是当纹理被应用到表面时。与像素的采样率相比，可以计算纹理样本的频率。如果该频率低于奈奎斯特频率限值，则不需要采取特殊措施来对纹理进行适当采样。如果频率太高，则使用各种算法对纹理进行频带限制(第6.2.2节)。

Reconstruction 重建

Given a band-limited sampled signal, we will now discuss how the original signal can be reconstructed from the sampled signal. To do this, a filter must be used. Three commonly used filters are shown in Figure 5.18. Note that the area of the filter should always be one, otherwise the reconstructed signal can appear to grow or shrink.

给定一个带限采样信号，我们现在将讨论如何从采样信号重构原始信号。为此，必须使用过滤器。三种常用的过滤器如图5.18所示。请注意，滤波器的面积应始终为1，否则重构信号可能会变大或变小。

Figure 5.18. The top left shows the box filter, and the top right the tent filter. The bottom shows the sinc filter (which has been clamped on the x-axis here). 

图5.18。左上角显示的是箱式过滤器，右上角显示的是帐篷式过滤器。底部显示的是sinc滤波器(此处已clamp在x轴上)。

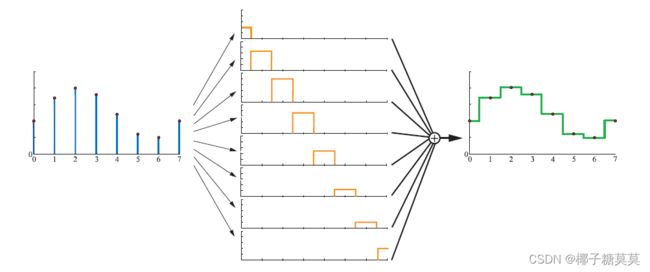
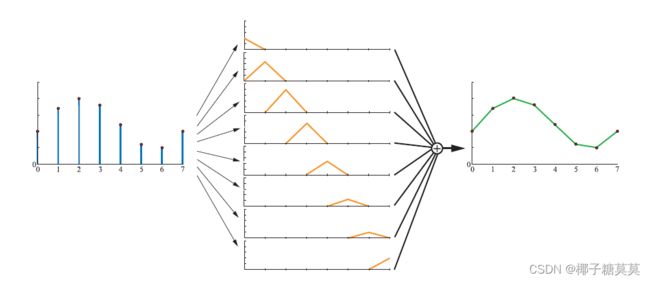
In Figure 5.19, the box filter (nearest neighbor) is used to reconstruct a sampled signal. This is the worst filter to use, as the resulting signal is a noncontinuous stair case. Still, it is often used in computer graphics because of its simplicity. As can be seen in the illustration, the box filter is placed over each sample point, and then scaled so that the topmost point of the filter coincides with the sample point. The sum of all these scaled and translated box functions is the reconstructed signal shown to the right.

在图5.19中，盒式滤波器(最近邻)用于重构采样信号。这是最不适合使用的滤波器，因为产生的信号是不连续的阶梯信号。尽管如此，由于其简单性，它还是经常被用于计算机图形学中。如图所示，盒式过滤器放置在每个采样点上，然后进行缩放，使过滤器的最高点与采样点重合。所有这些缩放和平移后的盒函数之和就是右边显示的重构信号。

Figure 5.19. The sampled signal (left) is reconstructed using the box filter. This is done by placing the box filter over each sample point, and scaling it in the y-direction so that the height of the filter is the same as the sample point. The sum is the reconstruction signal (right). 

图5.19。使用箱式滤波器重构采样信号(左)。这是通过将盒式过滤器放置在每个采样点上，并在y方向上缩放它，以便过滤器的高度与采样点相同。总和就是重建信号(右)。

The box filter can be replaced with any other filter. In Figure 5.20, the tent filter,also called the triangle filter, is used to reconstruct a sampled signal. Note that this filter implements linear interpolation between neighboring sample points, and so it is better than the box filter, as the reconstructed signal now is continuous.

箱式过滤器可以用任何其他过滤器替换。在图5.20中，帐篷滤波器，也称为三角滤波器，用于重构采样信号。注意，该滤波器在相邻采样点之间实现线性插值，因此它优于箱式滤波器，因为重构信号现在是连续的。

Figure 5.20. The sampled signal (left) is reconstructed using the tent filter. The reconstructed signal is shown to the right. 

图5.20。采样信号(左)使用帐篷滤波器重建。重建的信号显示在右侧。

However, the smoothness of the reconstructed signal using a tent filter is poor;there are sudden slope changes at the sample points. This has to do with the fact that the tent filter is not a perfect reconstruction filter. To get perfect reconstruction the ideal low-pass filter has to be used. A frequency component of a signal is a sine wave:sin(2πf), where f is the frequency of that component. Given this, a low-pass filter removes all frequency components with frequencies higher than a certain frequency defined by the filter. Intuitively, the low-pass filter removes sharp features of the signal, i.e., the filter blurs it. The ideal low-pass filter is the sinc filter (Figure 5.18 bottom):

然而，使用帐篷滤波器重构的信号的平滑度很差；在采样点有突然的斜率变化。这与帐篷滤波器不是完美的重建滤波器这一事实有关。为了获得完美的重建，必须使用理想的低通滤波器。信号的频率成分是正弦波:sin(2πf)，其中f是该成分的频率。鉴于此，低通滤波器会移除频率高于滤波器定义的特定频率的所有频率成分。直观上，低通滤波器去除了信号的尖锐特征，即滤波器使其模糊。理想的低通滤波器是sinc滤波器(图5.18底部):

 The theory of Fourier analysis [1447] explains why the sinc filter is the ideal lowpass filter. Briefly, the reasoning is as follows. The ideal low-pass filter is a box filter in the frequency domain, which removes all frequencies above the filter width when it is multiplied with the signal. Transforming the box filter from the frequency domain to the spatial domain gives a sinc function. At the same time, the multiplication operation is transformed into the convolution function, which is what we have been using in this section, without actually describing the term.

傅立叶分析理论[1447]解释了为什么sinc滤波器是理想的低通滤波器。简单来说，理由如下。理想的低通滤波器是频域中的箱式滤波器，当它与信号相乘时，会移除滤波器宽度以上的所有频率。将箱式滤波器从频域变换到空间域给出了sinc函数。同时，乘法运算被转化为卷积函数，这是我们在本节中一直使用的，没有实际描述该项。

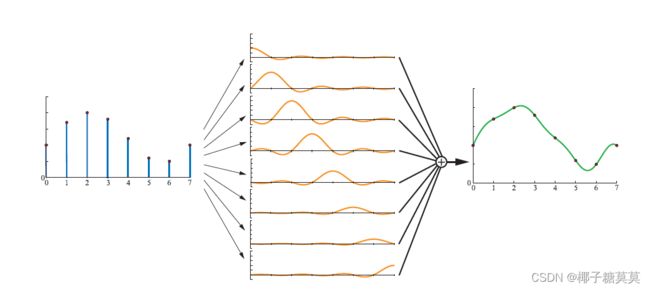
Using the sinc filter to reconstruct the signal gives a smoother result, as shown in Figure 5.21. The sampling process introduces high-frequency components (abrupt changes) in the signal, and the task of the low-pass filter is to remove these. In fact,the sinc filter eliminates all sine waves with frequencies higher than 1/2 the sampling rate. The sinc function, as presented in Equation 5.22, is the perfect reconstruction filter when the sampling frequency is 1.0 (i.e., the maximum frequency of the sampled signal must be smaller than 1/2). More generally, assume the sampling frequency is fs, that is, the interval between neighboring samples is 1/fs. For such a case, the perfect reconstruction filter is sinc(fsx), and it eliminates all frequencies higher than fs/2. This is useful when resampling the signal (next section). However, the filter width of the sinc is infinite and is negative in some areas, so it is rarely useful in practice.

使用sinc滤波器重构信号会产生更平滑的结果，如图5.21所示。采样过程会在信号中引入高频成分(突变)，低通滤波器的任务就是消除这些成分。事实上，sinc滤波器会消除频率高于1/2采样速率的所有正弦波。当采样频率为1.0(即采样信号的最大频率必须小于1/2)时，等式5.22所示的sinc函数是理想的重构滤波器。更一般地，假设采样频率为fs，即相邻样本之间的间隔为1/fs。对于这种情况，理想的重构滤波器是sinc(fsx ),它消除所有高于fs/2的频率。这在对信号进行重采样时非常有用(下一节)。然而，sinc的滤波器宽度是无限的，在某些区域为负值，因此在实践中很少使用。

Figure 5.21. Here, the sinc filter is used to reconstruct the signal. The sinc filter is the ideal low-pass filter. 

图5.21。这里，sinc滤波器用于重构信号。sinc滤波器是理想的低通滤波器。

There is a useful middle ground between the low-quality box and tent filters on one hand, and the impractical sinc filter on the other. Most widely used filter functions are between these extremes. All these filter functions have some approximation to the sinc function, but with a limit on how many pixels they influence. The filters that most closely approximate the sinc function have negative values over part of their domain. For applications where negative filter values are undesirable or impractical, filters with no negative lobes (often referred to generically as Gaussian filters, since they either derive from or resemble a Gaussian curve) are typically used. Section 12.1 discusses filter functions and their use in more detail.

一方面是低质量的箱式和帐篷式滤波器，另一方面是不实用的sinc滤波器，两者之间有一个有用的中间地带。最广泛使用的滤波函数介于这两个极端之间。所有这些滤波器函数都与sinc函数有些近似，但它们影响的像素数量有限。最接近sinc函数的滤波器在其部分范围内具有负值。对于负滤波器值不理想或不切实际的应用，通常使用没有负波段的滤波器(通常统称为高斯滤波器，因为它们源自或类似于高斯曲线)。第12.1节更详细地讨论了过滤函数及其使用。

After using any filter, a continuous signal is obtained. However, in computer graphics we cannot display continuous signals directly, but we can use them to resample the continuous signal to another size, i.e., either enlarging the signal, or diminishing it. This topic is discussed next.

使用任何滤波器后，都可以获得连续信号。然而，在计算机图形学中，我们不能直接显示连续的信号，但我们可以用它们把连续的信号重新采样成另一种尺寸，即放大或缩小信号。接下来讨论这个话题。

Resampling 重采样

Resampling is used to magnify or minify a sampled signal. Assume that the original sample points are located at integer coordinates (0, 1, 2, . . . ), that is, with unit intervals between samples. Furthermore, assume that after resampling we want the new sample points to be located uniformly with an interval a between samples. For a > 1,minification (downsampling) takes place, and for a < 1, magnification (upsampling) occurs.

重采样用于放大或缩小采样信号。假设原始采样点位于整数坐标(0, 1, 2, . . . )，即样本之间有单位间隔。此外，假设在重采样之后，我们希望新的样本点以样本之间的间隔a均匀地定位。大于1时，进行缩小(下采样),小于1时，进行放大(上采样)。

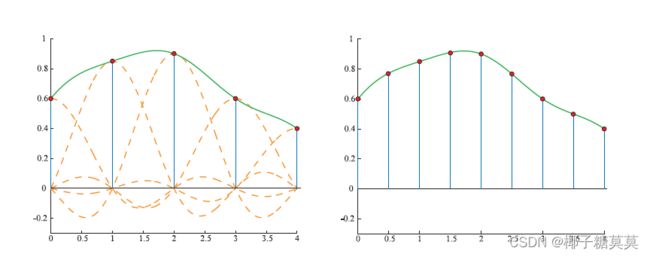
Magnification is the simpler case of the two, so let us start with that. Assume the sampled signal is reconstructed as shown in the previous section. Intuitively,since the signal now is perfectly reconstructed and continuous, all that is needed is to resample the reconstructed signal at the desired intervals. This process can be seen in Figure 5.22.

放大是两种情况中比较简单的一种，所以让我们从放大开始。假设采样信号按照上一节所示进行重构。直觉上，由于信号现在被完美地重构并且是连续的，所有需要的是以期望的间隔对重构的信号进行重新采样。这个过程可以在图5.22中看到。

Figure 5.22. On the left is the sampled signal, and the reconstructed signal. On the right, the reconstructed signal has been resampled at double the sample rate, that is, magnification has taken place. 

图5.22。左边是采样信号和重构信号。在右边，重构的信号已经以两倍的采样率被重新采样，也就是说，发生了放大。

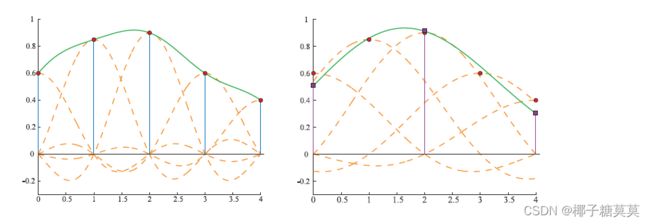
However, this technique does not work when minification occurs. The frequency of the original signal is too high for the sampling rate to avoid aliasing. Instead it has been shown that a filter using sinc(x/a) should be used to create a continuous signal from the sampled one. After that, resampling at the desired intervals can take place. This can be seen in Figure 5.23. Said another way, by using sinc(x/a) as a filter here, the width of the low-pass filter is increased, so that more of the signal’s higher frequency content is removed. As shown in the figure, the filter width (of the individual sinc’s) is doubled to decrease the resampling rate to half the original sampling rate. Relating this to a digital image, this is similar to first blurring it (to remove high frequencies) and then resampling the image at a lower resolution.

然而，当缩小发生时，这种技术不起作用。原始信号的频率对于避免锯齿的采样率来说太高了。相反，已经表明使用sinc(x/a)的滤波器应该用于从采样信号产生连续信号。之后，可以在期望的时间间隔进行重新采样。这可以在图5.23中看到。换句话说，通过使用sinc(x/a)作为滤波器，低通滤波器的宽度增加了，从而去除了更多的信号高频成分。如图所示,(单个sinc的)滤波器宽度加倍，以将重采样速率降至原始采样速率的一半。将此与数字图像联系起来，这类似于首先模糊它(以去除高频)，然后以较低的分辨率对图像进行重新采样。

Figure 5.23. On the left is the sampled signal, and the reconstructed signal. On the right, the filter
width has doubled in order to double the interval between the samples, that is, minification has taken place.

图5.23。左边是采样信号和重构信号。右边是过滤器 宽度加倍是为了使样本之间的间隔加倍，也就是说，发生了缩小。

With the theory of sampling and filtering available as a framework, the various algorithms used in real-time rendering to reduce aliasing are now discussed.

以采样和滤波理论作为框架，现在讨论实时渲染中使用的各种算法以减少锯齿。