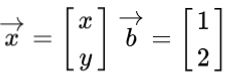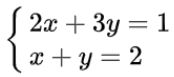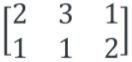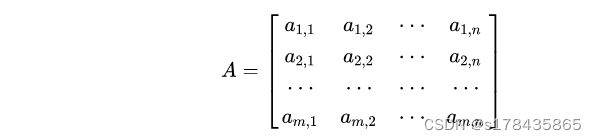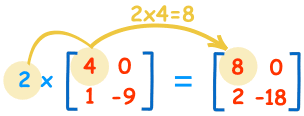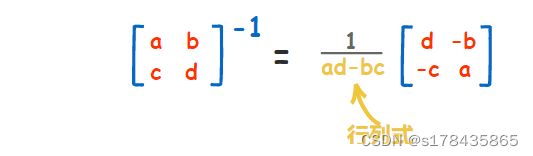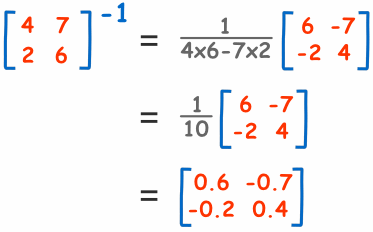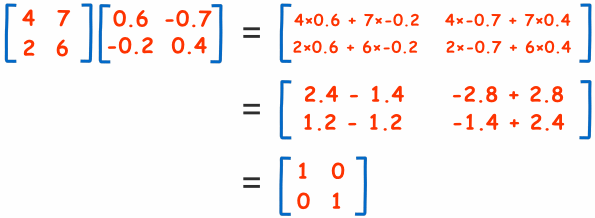1.3 矩阵运算

线性代数
线性方程

定义
线性方程是直线的方程
以下的都是线性方程：

y = 2x + 1

5x = 6 + 3y

y/2 = 3 − x

有很多不同的方式去写线性方程，他们通常有常数（像“2”或“c”），并且一定要有简单变量（像“x”或“y”）。

例，这些都是线性方程：

 

	y = 3x − 6
	y − 2 = 3(x + 1)
	y + 2x − 2 = 0
	5x = 6
	y/2 = 3

但线性方程的变量（像“x”或“y”）不能有：
●指数（像x2里的2）
●平方根、立方根等等
例，这些都不是线性方程：

	y2 − 2 = 0
	3√x − y = 6
	x3/2 = 16

斜截式
最常见的形式

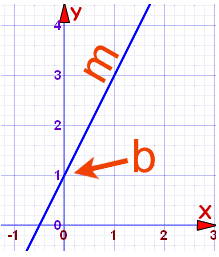
例子：y = 2x + 1
●坡度：m = 2
●截距：b = 1
直线图探索直线图的属性
点斜式
y − y1 = m(x − x1)

例子： y − 3 = (¼)(x − 2)
●x1 = 2
●y1 = 3
●m = ¼
一般式
Ax + By + C = 0（A 和 B 不能两者都等于 0）
例子：3x + 2y − 4 = 0
●A = 3
●B = 2
●C = −4
还有些别的不常见到的形式，具体参考线性方程
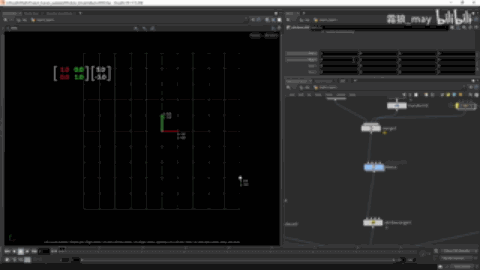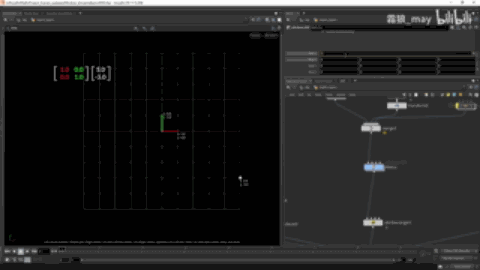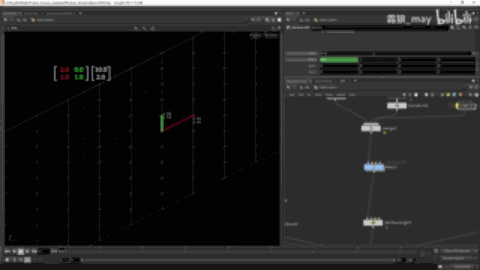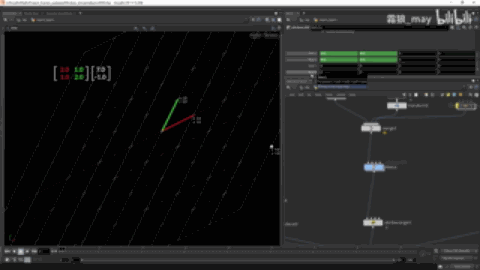
线性空间
直线变换后依然是直线，并且等比坐标原点保持不变
源：  【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili

变换前

变换后
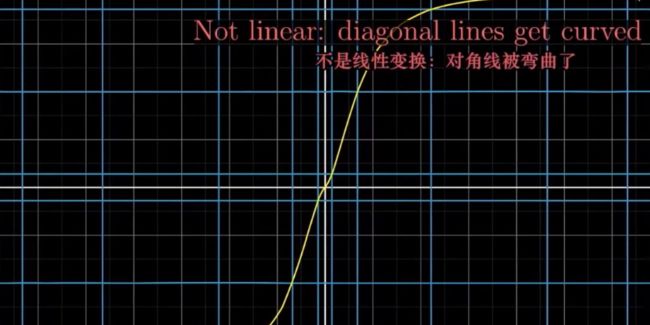
非线性空间
空间扭曲、不是等距、坐标原点有位移
源： 【官方双语/合集】线性代数的本质 - 系列合集_哔哩哔哩_bilibili

变换前

变换后
矩阵
矩阵的历史
矩阵最开始是用来解线性方程组的

将未知数x，y提出来，可以写成矩阵和向量的形式

其中

是矩阵，

是向量形式。
这样可以将线性方程组转化成一个向量方程，在已知矩阵A和向量

的情况下，求位置向量

矩阵的方式解线性方程组

将xy隐藏，并将等号右边的数字一起提出来，成为增广矩阵

和代数解方程一样，每行可以单独乘以系数或者每行相加减

可以先解一遍代数方程，同理解矩阵的方程，对比图如下

图解：

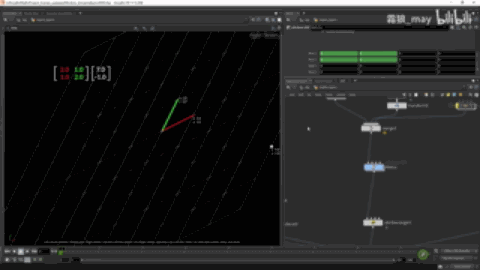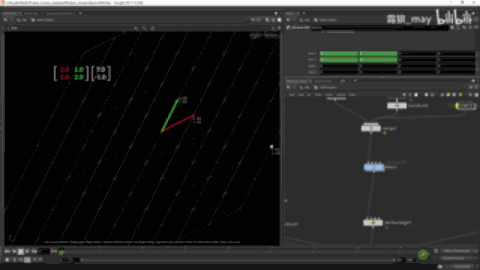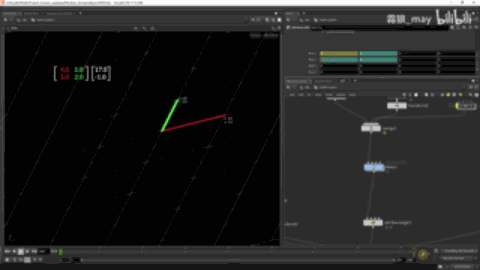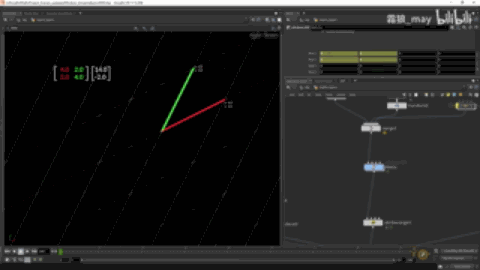
可以理解为解线性方程组就是将矩阵A转换成单位矩阵后得到的值。
例如上图在

{21​31​}

的坐标系上，点为（1,2），转换成单位矩阵的坐标系中点为（5，-3）。

此动态图录反了，图是由单位矩阵转到原始矩阵的
什么是矩阵
一个mxn的矩阵是一个由m行n猎元素排列成的矩形阵列。

矩阵的定义：由 m x n个数

aij​(i=1,2,3...m;j=1,2,3...n)

排成的 m 行 n 列的数表称为 m 行 n 列矩阵，简称 m x n 矩阵。为表示这些数字是一个整体，总是加一个方括号

 

特殊的矩阵
方阵：行数列数相等，切都等于n的矩阵称为n阶矩阵或n阶方阵

单位矩阵I：nxn矩阵，从左到右的对角线上的元素是1，其余元素都为0

零矩阵O：元素都是零的矩阵

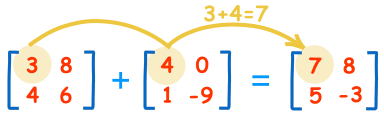
矩阵的加减法
把两个行列相等的矩阵才可以直接相加减。
矩阵的加法满足交换律和结合律
交换律    A+B = B+A
结合律    (A+B)+C=A+(B+C)

矩阵的减法
A-B = A+(-B)

注意：矩阵减法的定义实际是与负矩阵相加： A + (-B)
两个矩阵一定要大小相同，就是说，行要一样大小，列也要一样大小。
例子：具有3 行 和 5 列 的矩阵可以和另一个有 3 行 和 5 列的矩阵相加。但它不能和有 3 行 和 4 列 的矩阵相加（列的大小不同）。
几何意义：就是将两个不同的坐标系想加得到一个新的坐标系。
例如下图，单位矩阵和另一个矩阵想加得到新的坐标系

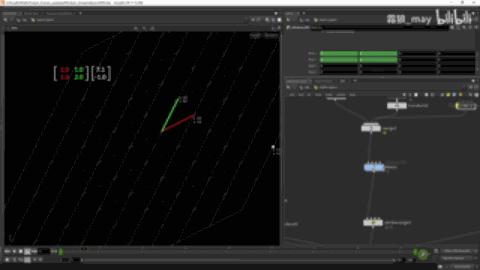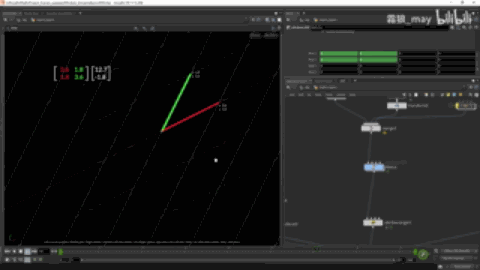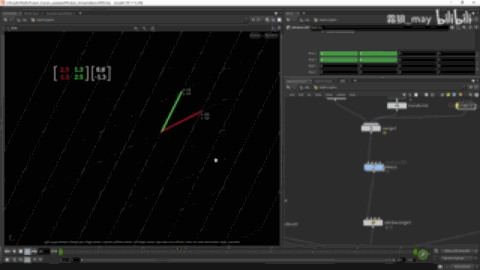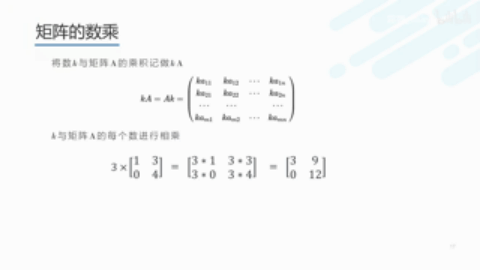
矩阵的数乘
将一个常数 k 与 矩阵A的乘积记做 kA

 

k与矩阵A的么个数进行相乘

我们称这常数为 标量，故此这乘法的正式名字是 "标量乘法"。
几何意义：空间（坐标系）的缩放。

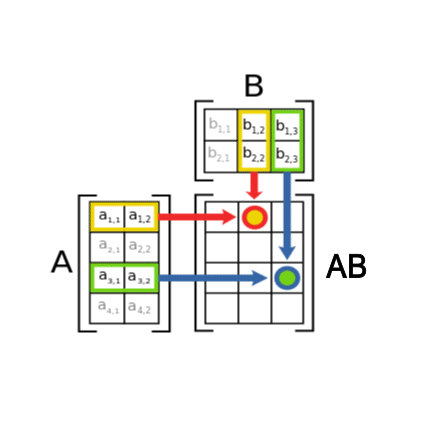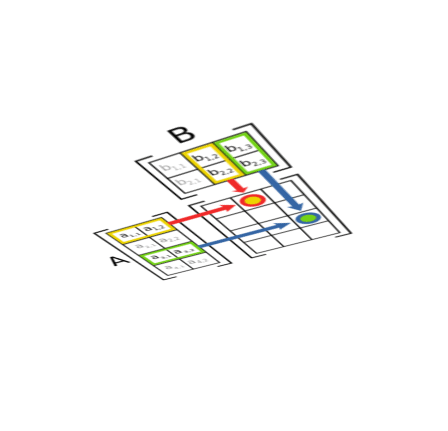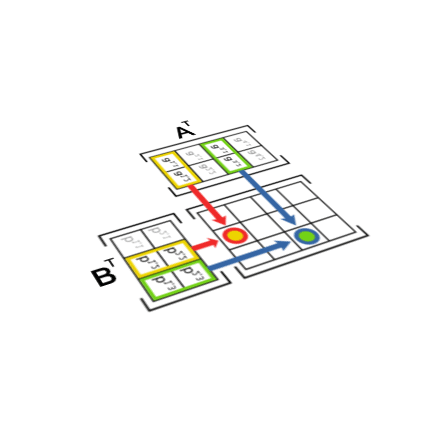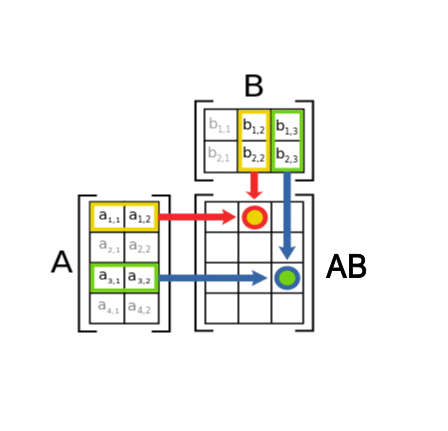
矩阵的乘法（重要）
更详细的解释：矩阵乘法
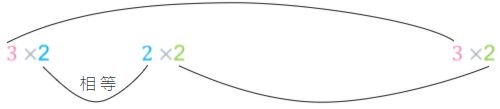
一般来说：
把m×n矩阵与n×p矩阵相乘，n 必须相同，相乘结果是m×p矩阵。

举例：

 

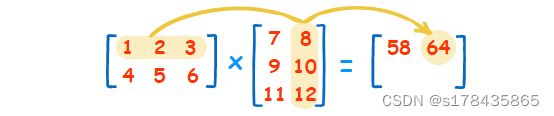
若要把矩阵与矩阵相乘，需要计算行与列的点积，例如

 

点积就是把对称的元素相乘，然后把结果加起来：
(1, 2, 3) • (7, 9, 11) = 1×7 + 2×9 + 3×11 = 58
我们把第一个元素相配（1 和 7），然后相乘。第二个元素（2 和 9） 和第三个元素（3 和 11）也一样，然后把结果加起来。
然后是第一行与第二列：

 

(1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64
第二行与第一列：
(4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139
第二行与第二列：
(4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

 

乘法次序：在矩阵乘法中没有乘法交换律一说（乘以单位矩阵除外）。
AB ≠ BA
举例：

矩阵乘法的几何意义

 

矩阵          矩阵         矩阵
一个矩阵叉乘另一个矩阵，得到的还是一个矩阵，但是这个矩阵在图形学上被称作变换矩阵
即 一个图形 进行 移动 + 旋转 + 缩放得到的是这个图形的变换矩阵，到最后这个样子需要将图形的原矩阵乘以变换矩阵

 

矩阵           向量        向量
一个矩阵与一个列向量相乘，得到的是我们想要的最后结果，即这个顶点变换之后的坐标。
在我们平时的实际开发中，我们不可能只单单对一个物体进行单个变换（移动，旋转，缩放），我们开始着手一个项目的时候往往是图形的复合变换，即包括图形的移动，旋转，缩放
在复合变换中我们采用的是列向量左乘

矩阵相乘的一个好处，我们可以除了最右边的向量不进行计算，先把左边的旋转，移动，缩放等先计算得到一个最终的变换矩阵，这时我们再拿最右边的向量与这个最终变换矩阵相乘得到最终结果。
1乘法结合律： (AB)C=A(BC)
2乘法左分配律：(A+B)C=AC+BC
3乘法右分配律：C(A+B)=CA+CB
4对数乘的结合性k(AB）=(kA)B=A(kB）
5转置 (AB)T=BTAT
6矩阵乘法在以下两种情况下满足交换律。
●AA*=A*A，A和伴随矩阵相乘满足交换律。
●AE=EA，A和单位矩阵或数量矩阵满足交换律。
特殊的矩阵

（演示视频地址： TA百人计划_矩阵_XerPhong_V02_哔哩哔哩_bilibili 24：58）

旋转矩阵推导
GAMSE101 也有个更巧妙的推导过程Lecture 03 Transformation_哔哩哔哩_bilibili 18：12

位移矩阵为什么是一个 3x3矩阵？答案是位移矩阵不是线性变换，是仿射变换，为什么是仿射变换？前面也说过线性变换原点是不会发生变化的，在位移变换中，原点已经发生了变化，所以我们需要多加一个维度

以上是二维空间的变换，下面是在三维空间中的坐标变换

unity中旋转矩阵是先绕z轴在绕x轴，最后再绕y轴进行计算的
动画演示TA百人计划_矩阵_XerPhong_V02_哔哩哔哩_bilibili 33:17
矩阵的转置
把矩阵A的航换成同序数的列，该操作成为矩阵的转置运算。
转置运算后可以得到一个新矩阵，改矩阵成为A的转置矩阵，记作AT

 

矩阵A转置的转置等于原来的矩阵A
转置矩阵的特性：

转置矩阵原理动态图
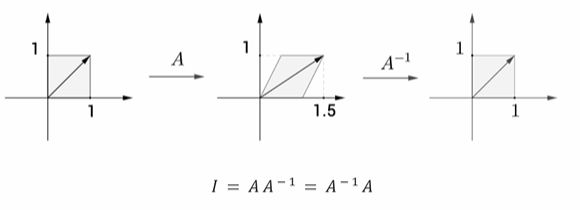
逆矩阵
更详细说明参考：逆矩阵
矩阵与它的逆矩阵相乘，得到单位矩阵。
常用作矩阵变换后再次矩阵变换会原来的初始位置。

求2x2矩阵的逆：

 

调换 a 和 d 的位置，把 负号放在 b 和 c 前面，然后全部除以矩阵的 行列式 （ad-bc）。

把矩阵与逆矩阵相乘来看是否为单位矩阵：

由此可得

为

矩阵的逆。
逆矩阵的运算规律：