我也是LeetCode周赛“三道题选手”啦 第270场周赛

我的Weekly Contest 270战况

参加周赛有7次了，1928/12931应该是目前最好一次排名了，上周的周赛和双周赛也是只做对3道题，我也是LeetCode周赛“三道题选手”啦。当然，离4道全AC的大佬们还有距离。

什么是LeetCode周赛？

刷LeetCode两年，我才发现leetcode上的算法题一直在更新，而且更新的题目的来源就是周赛（每周4题）和双周赛。

参加了几次，我的心得体会是：简单题不一定简单，中等/难题也不一定难，掌握会用常见套路，有了思路，再细心审题严谨分析。

show my code!

• 前三道都是新瓶装旧酒，或许第一道medium应该为easy，easy应该为medium难度。
• 第一题dfs全排列（47），很经典的题，不以0开头，偶数，三位数，加上去重，并不简单。
• 第二题，删除链表的中间节点，链表归并排序(https://leetcode.com/problems/sort-list/solution/)时就实现过，快慢指针，要删除中间节点，需要记录前驱节点。
• 第三题（2096），二叉树中两个节点的最短路径，依然可以从网上找到似曾相识的题，只不过题干有所改变，路径不再是节点的列表，而是每一步方向组成的字符串。
• 解法：
• 1、先求出两个节点的最近公共祖先（236)
• 2、分别求出公共祖先到两个节点的路径
• 3、根据两条路径拼接出方向字符串

2094. Finding 3-Digit Even Numbers

class Solution {
    private void dfs(int[] digits, boolean[] visited, int len, String cur, List<String> ans)
    {
        if(len == 1)
        {
            if(cur.charAt(0) == '0') return;
        }
        if(len == 3)
        {
            if(((cur.charAt(2) - '0') & 1) == 0)
            {
                ans.add(cur);
            }
            return;
        }
        
        for(int i = 0; i<digits.length; i++)
        {
            if(visited[i]) continue;
            if(i > 0 && digits[i] == digits[i-1] && !visited[i-1]) continue;
            visited[i] = true;
            dfs(digits, visited, len+1, cur+digits[i], ans);
            visited[i] = false; 
        }
    }
    
    public int[] findEvenNumbers(int[] digits) {
        Arrays.sort(digits);
        boolean[] visited = new boolean[digits.length];
        List<String> ans = new ArrayList<>();
        dfs(digits, visited, 0, "", ans);
        
        int[] nums = new int[ans.size()];
        for(int i=0; i<ans.size(); i++)
        {
            nums[i] = Integer.parseInt(ans.get(i));
        }
        return nums;
    }
}

2095. Delete the Middle Node of a Linked List

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode deleteMiddle(ListNode head) {
        if(head == null || head.next == null) return null;
        ListNode p = head;
        ListNode midPrev = null;
        while (p != null && p.next != null) {
            midPrev = (midPrev == null) ? p : midPrev.next;
            p = p.next.next;
        }
        midPrev.next = midPrev.next.next;
        return head;
    }
}

2096. Step-By-Step Directions From a Binary Tree Node to Another
用例1：
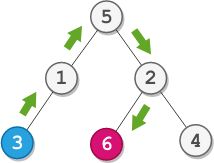用例2：

/**
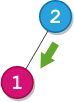
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public String getDirections(TreeNode root, int startValue, int destValue) {
        ArrayList<TreeNode> pathList1=new ArrayList<>();
        ArrayList<TreeNode> pathList2=new ArrayList<>();
        //求出两个节点的最近公共祖先
        TreeNode ancestor=lowestCommonAncestor(root, startValue, destValue);
        //分别求出公共祖先到两个节点的路经
        getPath(ancestor,startValue,pathList1);
        getPath(ancestor,destValue,pathList2);
        
        StringBuilder sb = new StringBuilder();
        for(int i=0; i<pathList1.size()-1; i++)
        {
            sb.append("U");
        }
        for(int i=0; i<pathList2.size()-1; i++)
        {
            TreeNode pnt = pathList2.get(i);
            TreeNode cid = pathList2.get(i+1);
            if(pnt.left == cid) sb.append("L");
            else sb.append("R");
        }
        return sb.toString();
    }
    
    public TreeNode lowestCommonAncestor (TreeNode root, int node1, int node2){
        if (root==null || root.val==node1 || root.val==node2) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,node1,node2);
        TreeNode right = lowestCommonAncestor(root.right, node1, node2);
        if(left != null && right != null) { 
            return root;
        }
        return left==null?right:left; 
    }

    /**
     *  获取祖先节点到目标节点的路经（包含祖先节点和目标节点）
     */
    public boolean getPath(TreeNode root,int target,ArrayList<TreeNode> pathList){
        pathList.add(root);          
        if (root.val == target) {
            return true; 
        }         
        boolean hasFound=false;
        if (root.left!=null)
            hasFound=getPath(root.left,target,pathList);
        if (!hasFound && root.right!=null)
            hasFound=getPath(root.right,target,pathList);
        if (!hasFound)
            pathList.remove(pathList.size()-1);
        return hasFound; 
    }
}

复盘解决Hard题

2097. Valid Arrangement of Pairs
比赛结束后，官网有解题提示，正好学习一波。

欧拉回路：从起点出发，每条边走一遍，遍历所有结点和边后回到起点，这个路径称为欧拉回路。
找欧拉回路的Hierholzer算法思路如下：

The algorithm assumes that the given graph has a Eulerian Circuit.

• Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because indegree and outdegree of every vertex must be same, when the trail enters another vertex w there must be an unused edge leaving w.
  The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
• 上面的一段，大意是从结点v dfs直到回到v，但一次dfs可能不会遍历完所有结点和边。
• As long as there exists a vertex u that belongs to the current tour, but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour.
• 回溯，上一步的路径上存在结点u还有未访问的边, 从结点u出发，访问所有未访问的边能回到u。和之前的路径汇合形成欧拉回路。
• 算法的具体实现可参照题解的dfs方法，其中ans是逆序的欧拉回路路径。

private void dfs(int start)
{
     List<Integer> edges = graph.get(start);
     if(edges == null) return;
     while(edges.size() > 0)
     {
         int next = edges.get(edges.size()-1);
         edges.remove(edges.size()-1);
         dfs(next);
         //when next has not adjoin edge, 
         //add [start, next] to ans
         ans.add(new int[]{start, next});
     }
}

那么，这一题与欧拉回路稍许不同的是，遍历完所有的边不一定回到起点。
那么，dfs的起点就不能随意指定，而是要找（出度>入度）的节点作为起点，如果不存在，则按照欧拉回路的解法随意指定起点，如pairs[0][0]。

class Solution {
    Map<Integer, List<Integer>> graph;
    Map<Integer, Integer> degree;
    List<int[]> ans;
    
    public int[][] validArrangement(int[][] pairs) {
        graph = new HashMap<>();
        ans = new ArrayList<>();
        degree = new HashMap<>();
        
        //build graph
        buildGraph(pairs);
        
        //select a start
        int start = -1;
        for(Integer i : degree.keySet())
        {
            if(degree.get(i) > 0)
            {
                start = i;
                break;
            }
        }
        
        if(start == -1) start = pairs[0][0];
        
        //dfs Hierholzer
        dfs(start);
        
        int size = ans.size();
        int[][] range = new int[size][2];
        for(int i=0; i<size; i++)
        {
            range[i][0] = ans.get(size-1-i)[0];
            range[i][1] = ans.get(size-1-i)[1];
        }
        return range;
    }
    
    private void buildGraph(int[][] pairs)
    {
        for(int[] pair : pairs)
        {
            graph.putIfAbsent(pair[0], new ArrayList<>());
            List<Integer> edges = graph.get(pair[0]);
            edges.add(pair[1]);
            
            int cnt = degree.getOrDefault(pair[0], 0);
            degree.put(pair[0], cnt+1);
            cnt = degree.getOrDefault(pair[1], 0);
            degree.put(pair[1], cnt-1);
        }
    }
    
    private void dfs(int start)
    {
        List<Integer> edges = graph.get(start);
        if(edges == null) return;
        while(edges.size() > 0)
        {
            int next = edges.get(edges.size()-1);
            edges.remove(edges.size()-1);
            dfs(next);
            //when next has not adjoin edge, 
            //add [start, next] to ans
            ans.add(new int[]{start, next});
        }
    }
}