zzzyyzz_
zzzyyzz_

牛客小白月赛75 DE

                                                      D  矩阵

登录—专业IT笔试面试备考平台_牛客网

牛客小白月赛75 DE_第1张图片

思路：我们能够发现每个点最多只用两种状态，一种是不变，另一种是改变，如果相邻的点与当前点不相同，则可以花费一个单位走过去，否则需要先改变它的状态，然后走过去，能够发现这是一个分层图，一共只有两层，我们直接在分层图上用dijkstra跑最短路即可，当与当前点相邻的点与当前点相同时，距离为2，否则距离为1

// Problem: 矩阵
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/60063/D
// Memory Limit: 524288 MB
// Time Limit: 2000 ms

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair PII;
typedef pair > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
char str[1010][1010];
int dist[1010][1010][2];
bool st[1010][1010][2];
int dx[]={-1,1,0,0},dy[]={0,0,-1,1};

struct Node{
	int x,y;
	int ans;
	int temp;
};

void dijkstra() {
	memset(dist,0x3f,sizeof dist);
	
	queue q;
	q.push({1,1,0,str[1][1]-'0'});
	dist[1][1][str[1][1]-'0']=0;
	
	while(q.size()) {
		auto it=q.front();
		q.pop();
		
		int x=it.x,y=it.y,k=it.temp;
		if(st[x][y][k]) continue;
		st[x][y][k]=true;
		
		for(int i=0;i<4;i++) {
			int tx=x+dx[i],ty=y+dy[i];
			if(tx<1||tx>n||ty<1||ty>m) continue;
			if(k==str[tx][ty]-'0') {
				if(dist[tx][ty][k^1]>dist[x][y][k]+2) {
					dist[tx][ty][k^1]=dist[x][y][k]+2;
					q.push({tx,ty,dist[tx][ty][k^1],k^1});
				}
			}else {
				if(dist[tx][ty][str[tx][ty]-'0']>dist[x][y][k]+1) {
					dist[tx][ty][str[tx][ty]-'0']=dist[x][y][k]+1;
					q.push({tx,ty,dist[tx][ty][str[tx][ty]-'0'],str[tx][ty]-'0'});
				}
			}
		}
	}
}

void solve() {
	n=read(),m=read();
	
	for(int i=1;i<=n;i++) scanf("%s",str[i]+1);
	
	dijkstra();
	
	printf("%d\n",min(dist[n][m][0],dist[n][m][1]));
}   

int main() {
    // init();
    // stin();

    // scanf("%d",&T);
    T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}

                                                                 E 数数

登录—专业IT笔试面试备考平台_牛客网

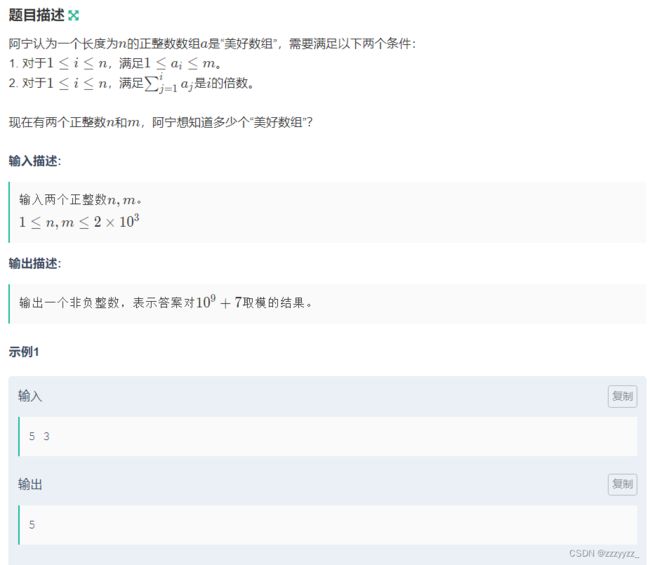
牛客小白月赛75 DE_第2张图片

思路：其实能够发现这是一个ｄｐ问题，因为如果我知道了当前的总和是什么，当前这个位置方哪个数，那么我们就可以根据前面的状态求出来，一开始是用f[i][j]表示的是只用前i个，并且总和是j的方案数，不仅超时而且还不对，看了题解发现可以f[i][j]表示只使用前ｉ个并且总和为i*j的方案数，因为一定要保证前缀和是ｉ的倍数，假设前ｉ－１个数的和为(i-1)*k，第ｉ个数为t,那么我们能够得到(i-1)*k+t=i*j，能够得到ｔ的值，又因为１＜＝ｔ＜＝ｍ，将前式解的的解带入后面能够接出来一个ｋ的范围，（i*j-m+i-2)/(i-1)<=k<=(i*j-1)/(i-1)，如果我们知道了ｉ，ｊ那么我们就知道了满足条件的ｋ的范围，那么f[i][j]就能够通过f[i-1][k]求和得到

// Problem: 数数
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/60063/E
// Memory Limit: 524288 MB
// Time Limit: 2000 ms

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair PII;
typedef pair > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}

int T,hackT;
int n,m,k;
int f[1010][1010];	
int sum[1010];

void solve() {
	n=read(),m=read();
	
	for(int i=1;i<=m;i++) f[1][i]=1;
	
	for(int i=2;i<=n;i++) {
		for(int j=1;j<=m;j++) sum[j]=(sum[j-1]+f[i-1][j])%mod;
		for(int j=1;j<=m;j++) {
			int l=(i*j-m+i-2)/(i-1),r=(i*j-1)/(i-1);
			l=max(l,1),r=min(r,m);
			f[i][j]=(sum[r]-sum[l-1]+mod)%mod;
		}
	}
	
	ll res=0;
	for(int i=1;i<=m;i++) res=(res+f[n][i])%mod;
	
	write(res);
}   

int main() {
    // init();
    // stin();

    // scanf("%d",&T);
    T=1; 
    while(T--) hackT++,solve();
    
    return 0;       
}

  

你可能感兴趣的:(图论,算法)

  • 图解数据结构python读书笔记_python cookbook3读书笔记第一章数据结构和算法 eternal?
    pythonheapq模块查询一组序列中最大和最小的数据importheapqnums=[1,8,2,23,7,-4,18,23,42,37,]#获取序列中3个最大值#print(heapq.nlargest(3,nums))#获取序列中3个最小值#print(heapq.nsmallest(3,nums))#把数据压入堆中在堆中最小的那个数值永远排在最前面时间想取出最小的3个数值只需执行3次he
  • 求任意两顶点间最短路算法及其matlab程序详解 夏天天天天天天天# 图论算法图论matlab
    #################本文为学习《图论算法及其MATLAB实现》的学习笔记#################算法用途图中任意两点间最短路的求法算法思想利用求最短路的Floyd算法的思想。首先,求得最短距离矩阵;然后,求任意给定两个顶点间的最短路所包含的顶点。程序参数说明W:图的权值矩阵k1:始点k2:终点P:k1，k2之间的最短路，顶点以经过次序排列u:最短路的距离算法的matlab程
  • Open3D mesh 拉普拉斯laplacian滤波 白葵新 3d算法python计算机视觉人工智能
    目录一、概述1.1原理1.2实现步骤1.3应用场景二、代码实现2.1关键函数参数详解返回值2.2完整代码三、实现效果3.1加入噪点的mesh3.2迭代10次3.3迭代100次Open3D点云算法汇总及实战案例汇总的目录地址：Open3D点云算法与点云深度学习案例汇总（长期更新）-CSDN博客一、概述拉普拉斯滤波（LaplacianSmoothing）是一种常用的网格平滑技术，通过对网格顶点的位置进
  • Windows下快速安装Open3D-0.18.0(python版本)详细教程 白葵新 python计算机视觉算法图像处理windows3d
    目录一、Open3D简介1.1主要用途1.2应用领域二、安装Open3D2.1激活环境2.2安装open3d2.3测试安装是否成功三、测试代码3.1代码3.2显示效果Open3D专栏算法目录Open3D点云算法与点云深度学习案例汇总（长期更新）-CSDN博客一、Open3D简介Open3D是一个强大的开源库，专门用于处理和可视化3D数据，如点云、网格和RGB-D图像。它提供了丰富的功能和工具，广泛
  • Open3D 点云配准-Ransac算法（粗配准） 白葵新 算法人工智能python计算机视觉图像处理3d
    目录一、概述1.1简介1.2RANSAC在点云粗配准中的应用步骤二、代码实现2.1关键函数2.2完整代码2.3代码解析2.3.1计算FPFH1.法线估计2.计算FPFH特征2.3.2全局配准1.函数：execute_global_registration2.距离阈值3.registration_ransac_based_on_feature_matching函数三、实现效果3.1原始点云3.2配准
  • 119 杨辉三角 II YyyyyMC
    题目：题目链接给定一个非负索引k，其中k≤33，返回杨辉三角的第k行。在杨辉三角中，每个数是它左上方和右上方的数的和示例:输入:3输出:[1,3,3,1]进阶：你可以优化你的算法到O(k)空间复杂度吗？解题思路：题目中的返回要求是某一行的所有数据第一个思路是把每一行的数据都求出来，直到要求的行为止这样就太过于繁琐，效率相当的低第二个思路是通过递归求每一位上的数，同时达到了进阶要求的O(k)的空间复
  • 算法推荐规制！《互联网信息服务算法推荐管理规定（征求意见稿）》公开征求意见 AIwenIPgeolocation 网络安全
    互联网信息服务算法推荐管理规定（征求意见稿）第一条为了规范互联网信息服务算法推荐活动，维护国家安全和社会公共利益，保护公民、法人和其他组织的合法权益，促进互联网信息服务健康发展，弘扬社会主义核心价值观，根据《中华人民共和国网络安全法》、《中华人民共和国数据安全法》、《中华人民共和国个人信息保护法》、《互联网信息服务管理办法》等法律、行政法规，制定本规定。第二条在中华人民共和国境内应用算法推荐技术提
  • 云计算实训09——rsync远程同步、自动化推取文件、对rsyncd服务进行加密操作、远程监控脚本 是小赵鸭. linux服务器云计算深度学习
    一、rsync远程同步1.rsync基本概述（1）sync同步（2）async异步（3）rsync远程同步2.rsync的特点可以镜像保存整个目录树和文件系统可以保留原有权限，owner,group,时间，软硬链接，文件acl,文件属性等传输效率高，使用同步算法支持匿名传输，方便网站镜像，安全性高3、rsync与scp的区别两者都可以实现远程同步，但是相对⽐⽽⾔，rsync能⼒更强①⽀持增量备份②
  • 【Tools】计算机视觉（CV）技术的优势和挑战。 音乐学家方大刚 工具计算机视觉人工智能
    我们从不正视那个问题那一些是非题总让人伤透脑筋我会期待爱盛开那一个黎明一定会有美丽的爱情范玮琪《是非题》计算机视觉（CV）技术是一种模拟人类视觉系统的能力，通过使用计算机算法和图像处理技术，让计算机能够理解和解释图像和视频。它在许多领域都有广泛的应用，包括医疗诊断、安全监控、自动驾驶、人脸识别等。下面是计算机视觉技术的优势和挑战的一些例子：优势：高速处理：计算机视觉可以快速处理大量的图像和视频数据
  • 【大数据】孤立森林算法 大雨淅淅 大数据算法python大数据人工智能
    目录一、孤立森林算法概述二、孤立森林算法优缺点和改进2.1孤立森林算法优点2.2孤立森林算法缺点2.3孤立森林算法改进三、孤立森林算法代码实现3.1孤立森林算法python实现3.2孤立森林算法JAVA实现3.3孤立森林算法C++实现四、孤立森林算法应用一、孤立森林算法概述孤立森林算法是一种用于异常检测的机器学习算法。它基于这样的直觉：异常点是数据中的少数派，它们在特征空间中的分布与正常数据点不同
  • arcgis10之将多个栅格数据合并成一个含有多波段的栅格数据 xuxu1116 shparcgis实战教程arcgisshp栅格栅格合并
    如果觉得波段名称不满意，可以右击波段进行重命名即可。整理了完整版软件使用方法，关注公众号‘CV算法小屋’，获取软件更多使用方法
  • Python算法模糊匹配：FuzzyWuzzy深度剖析，从入门到精通，解决你所有需要匹配的需求 长风清留扬 Python人工智能算法python算法大数据网络dba
    在数据科学与机器学习的广阔领域中，处理不精确或模糊的数据是一项至关重要的技能。想象一下，当你面对的是一堆拼写错误、缩写、或是格式不一的文本数据时，如何高效地从中提取有价值的信息？这正是FuzzyWuzzy——Python中一个强大的模糊字符串匹配库，能够大展身手的地方。本文将为你全面介绍FuzzyWuzzy——Python中一个强大的通过算法模糊字符串匹配库，全网最全最新，一看就会，接下来带你走进
  • 计算机专业软件工程毕业设计做什么简单 李哥讲程序开发 软件工程课程设计毕业设计springbootjavavue
    软件工程毕业设计选择简单又实用的项目可以**管理系统的设计与开发、基于算法的设计（有些骗难度）、微信小程序的开发等**。具体选择哪些项目，还要根据个人兴趣和所学知识来决定。以下是一些建议：1.**管理系统的设计与开发**：（推荐）-如学生管理系统、图书馆管理系统等，这类题目通常需求明确，涉及的基础功能如登录、注册、数据管理等较为简单，容易实现。-示例题目：基于SpringBoot的实验室资产管理系
  • unity3D学习笔记之三：全局光照 watl0 UnityUnity
    本文整理自Unity全球官方网站，原文：UNITY5-LIGHTINGANDRENDERING（文章较长，请耐心阅读）简介全局光照，简称GI，是一个用来模拟光的互动和反弹等复杂行为的算法，要精确的仿真全局光照非常有挑战性，付出的代价也高，正因为如此，现代游戏会先一定程度的预先处理这些计算，而非游戏执行时实时运算。同一场景里：没有照明(左)，只有直接光源(中)，和有间接光源的全局光照(右)的表现，注
  • 代码随想录算法训练营day18 || 513.找树左下角的值，112.路径总和，106.从中序和后序序列构造二叉树 weixin_44316285 算法
    视频链接：怎么找二叉树的左下角？递归中又带回溯了，怎么办？|LeetCode：513.找二叉树左下角的值_哔哩哔哩_bilibili拿不准的遍历顺序，搞不清的回溯过程，我太难了！|LeetCode：112.路径总和_哔哩哔哩_bilibili坑很多！来看看你掉过几次坑|LeetCode：106.从中序与后序遍历序列构造二叉树_哔哩哔哩_bilibili513.找树左下角的值思路：题目的目标是找最底
  • unity光照技术 TheAI
    简介全局光照，简称GI，是一个用来模拟光的互动和反弹等复杂行为的算法，要精确的仿真全局光照非常有挑战性，付出的代价也高，正因为如此，现代游戏会先一定程度的预先处理这些计算，而非游戏执行时实时运算。同一场景里：没有照明(左)，只有直接光源(中)，和有间接光源的全局光照(右)的表现，注意颜色如何在不同的表面进行光的”反弹”，产生更真实的结果。在本文中，我们会描述全局光照如何在Unity里运作，带领你通
  • Unity 光照技术小结 布尔君de二次方 Unity3D
    原文自Unity全球官方网站，原文：UNITY5-LIGHTINGANDRENDERING简介全局光照，简称GI，是一个用来模拟光的互动和反弹等复杂行为的算法，要精确的仿真全局光照非常有挑战性，付出的代价也高，正因为如此，现代游戏会先一定程度的预先处理这些计算，而非游戏执行时实时运算。同一场景里：没有照明(左)，只有直接光源(中)，和有间接光源的全局光照(右)的表现，注意颜色如何在不同的表面进行光
  • 算法day17|如何求普通二叉树的众数 桃酥403 算法数据结构c++leetcode哈希算法
    算法day17|如何求普通二叉树的众数501的变式：普通二叉树的众数501的变式：普通二叉树的众数如果把二叉搜索树变成普通二叉树，我们该怎么思考呢？这个时候就要回到我一开始的思路了，用哈希表来解决问题。classSolution{public:unordered_mapmap;voidtraversal(TreeNode*root){if(root==nullptr)return;map[root
  • 算法day13|226.翻转二叉树、101. 对称二叉树、104.二叉树的最大深度、111.二叉树的最小深度 桃酥403 算法数据结构c++leetcode
    算法day13|226.翻转二叉树、101.对称二叉树、104.二叉树的最大深度、111.二叉树的最小深度226.翻转二叉树101.对称二叉树104.二叉树的最大深度111.二叉树的最小深度226.翻转二叉树第一次做没做出来，看了卡哥的视频，我很疑惑：翻转和前中后序遍历有什么关系呢？其实，所谓的遍历顺序，也就是处理的顺序，其目的不在于把它遍历出来，而是给出一个等待处理的顺序或者说将二叉树转换成了类
  • 数据结构（邓俊辉）学习笔记】串 10——BM_BC算法：坏字符 诸葛悠闲 数据结构学习笔记
    文章目录1.坏字符2.特殊情况1.坏字符实际上，刚才的实例中我们所展示的那样一个计算过程，就是所谓BM算法所采用的策略之一，而这一策略，将我们刚才所说的教训称作坏字符。在这里，不妨改为基于蛮力算法的第二个版本来进行改造。也就是说模式算中当前参与比对的如果是字符P[j]，那么文本串中对应的就是T[i+j]，这幅图画出的就是这样一个一般性的场景。请注意，当前这趟扫描如果的确已经抵达P[j]或T[i+j
  • 克鲁斯卡尔算法基本使用方法及相关示例 安星不会码字 算法c++数据结构
    这个算法是基于并查集，然后结合了贪心思想；我使用正确发过的一个题作为例子；完整代码见文章：公路村村通先用一个结构体来存储两个城镇的编号及相关费用；然后写一个并查集模板，前面也有发的；具体情况就是这样：typedefstruct{intu,v,w;}WW;intp[1001];intfind(intx){if(p[x]==x)returnx;elsereturnp[x]=find(p[x]);}该算
  • 经典算法：双指针问题--数组合并 Franda914 数据结构与算法指针算法数据结构列表python
    算法—程序的灵魂，没错就是灵魂！今天我们来聊聊关于双指针问题中的数组合并问题内容参考：《你也能看得懂的Python算法书》转载请标注：https://blog.csdn.net/qq_43582207python版本：Python3.7IDE：Jupyternotebook作者:Myapologize文章目录双指针问题数组合并1.合并有序数组双指针问题首先介绍一个概念：“指针”，他是编程语言中的一
  • 算法 遥远的清平湾
    http://ctan.mirror.colo-serv.net/macros/latex/contrib/algorithmicx/algorithmicx.pdf
  • windows系统huggingface连接不上的解决方案 herosunly windowshuggingface连接不上解决方案
      大家好，我是herosunly。985院校硕士毕业，现担任算法研究员一职，热衷于大模型算法的研究与应用。曾担任百度千帆大模型比赛、BPAA算法大赛评委，编写微软OpenAI考试认证指导手册。曾获得阿里云天池比赛第一名，CCF比赛第二名，科大讯飞比赛第三名。授权多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法行业就业。希望和大家一起成长进步。  
  • 迪杰斯特拉(Dijkstra's )算法——解决带权有向无向图最短路径 一条晒干的咸魚 数据结构与算法算法
    迪杰斯特拉算法(Dijkstra'sAlgorithm)，又称为狄克斯特拉算法，是一种用于解决带权重有向图或无向图最短路径问题的算法。该算法由荷兰计算机科学家艾兹赫尔·狄克斯特拉在1956年发明，是一种广泛应用于网络路由和其他领域的算法。在2001年的一次采访中，Dijkstra博士透露了他设计这个算法的起因和过程：从Rotterdam到Groningen的最短路线是什么？我花了大概20分钟时间设
  • 弗洛伊德(Floyd's)算法—解决最短路径经典算法 一条晒干的咸魚 数据结构与算法算法
    弗洛伊德算法(Floyd'salgorithm)是一种用于解决图中最短路径问题的经典算法。由美国计算机科学家罗伯特·弗洛伊德于1962年提出，该算法通过动态规划的思想，在图中寻找任意两个节点之间的最短路径，具有广泛的应用。本文将详细介绍弗洛伊德算法的原理、实现细节以及应用案例。一、原理动态规划思想：弗洛伊德算法利用了动态规划的思想，将原问题分解为子问题并进行逐步求解。它通过不断更新节点之间的最短路
  • 游卡，三七互娱，得物，顺丰，快手，oppo，莉莉丝，康冠科技，途游游戏，埃科光电25秋招内推 2401_86288678 算法前端javac语言python
    游卡，三七互娱，得物，顺丰，快手，oppo，莉莉丝，康冠科技，途游游戏，埃科光电25秋招内推①顺丰【招聘岗位】研发、算法、大数据、产品、项管、设计、人资等【官方内推码】4FOLXH【一键内推】https://sourl.cn/UzbDat②游卡【岗位】程序技术、产品策划、美术、发型运营、职能综合、桌游业务等大类【一键内推】https://sourl.cn/PHiZZE【内推码】DSymte2c③得
  • github源码指引：共享内存、数据结构与算法：平衡二叉树set带有互斥接口的 初级代码游戏 github源码指引共享内存数据结构与算法github哈希算法算法共享内存
    初级代码游戏的专栏介绍与文章目录-CSDN博客我的github：codetoys，所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。这些代码大部分以Linux为目标但部分代码是纯C++的，可以在任何平台上使用。目录一、演示代码二、互斥层的实现2.1简单的互斥层实现2.2完整互斥接口的实现2.2.1互斥对象放在哪里2.2.2迭代器的互斥2.2.3方法的互斥三、互斥层的设计思想一、演示
  • 游卡，三七互娱，得物，顺丰，快手，oppo，莉莉丝，康冠科技，途游游戏，埃科光电25秋招内推 2401_86288678 python算法c语言java前端
    游卡，三七互娱，得物，顺丰，快手，oppo，莉莉丝，康冠科技，途游游戏，埃科光电25秋招内推①顺丰【招聘岗位】研发、算法、大数据、产品、项管、设计、人资等【官方内推码】4FOLXH【一键内推】https://sourl.cn/UzbDat②游卡【岗位】程序技术、产品策划、美术、发型运营、职能综合、桌游业务等大类【一键内推】https://sourl.cn/PHiZZE【内推码】DSymte2c③得
  • github源码指引：共享内存、数据结构与算法：平衡二叉树set的lower_bound 初级代码游戏 github源码指引共享内存数据结构与算法github哈希算法算法
    初级代码游戏的专栏介绍与文章目录-CSDN博客我的github：codetoys，所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。这些代码大部分以Linux为目标但部分代码是纯C++的，可以在任何平台上使用。本篇专门讲解lower_bound的实现。目录一、STL的lower_bound和upper_bound是什么二、二叉树有没有lower_bound三、演示代码3.1定义数据
  • jsonp 常用util方法 hw1287789687 jsonpjsonp常用方法jsonp callback
    jsonp 常用java方法 (1)以jsonp的形式返回:函数名(json字符串) /*** * 用于jsonp调用 * @param map : 用于构造json数据 * @param callback : 回调的javascript方法名 * @param filters : <code>SimpleBeanPropertyFilter theFilt
  • 多线程场景 alafqq 多线程
    0 能不能简单描述一下你在java web开发中需要用到多线程编程的场景？0 对多线程有些了解，但是不太清楚具体的应用场景，能简单说一下你遇到的多线程编程的场景吗？ Java多线程 2012年11月23日 15:41 Young9007 Young9007 4 0 0 4 Comment添加评论关注(2) 3个答案 按时间排序 按投票排序 0 0 最典型的如： 1、
  • Maven学习——修改Maven的本地仓库路径 Kai_Ge maven
          安装Maven后我们会在用户目录下发现.m2 文件夹。默认情况下，该文件夹下放置了Maven本地仓库.m2/repository。所有的Maven构件(artifact)都被存储到该仓库中，以方便重用。但是windows用户的操作系统都安装在C盘，把Maven仓库放到C盘是很危险的，为此我们需要修改Maven的本地仓库路径。    
  • placeholder的浏览器兼容 120153216 placeholder
    【前言】 自从html5引入placeholder后，问题就来了， 不支持html5的浏览器也先有这样的效果， 各种兼容，之前考虑，今天测试人员逮住不放， 想了个解决办法，看样子还行，记录一下。   【原理】 不使用placeholder，而是模拟placeholder的效果， 大概就是用focus和focusout效果。   【代码】 <scrip
  • debian_用iso文件创建本地apt源 2002wmj Debian
    1.将N个debian-506-amd64-DVD-N.iso存放于本地或其他媒介内，本例是放在本机/iso/目录下 2.创建N个挂载点目录 如下： debian:~#mkdir –r /media/dvd1 debian:~#mkdir –r /media/dvd2 debian:~#mkdir –r /media/dvd3 …. debian:~#mkdir –r /media
  • SQLSERVER耗时最长的SQL 357029540 SQL Server
    对于DBA来说，经常要知道存储过程的某些信息： 1.   执行了多少次 2.   执行的执行计划如何 3.   执行的平均读写如何 4.   执行平均需要多少时间 列名          &
  • com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 7454103 eclipse
    今天eclipse突然报了com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 错误，并且工程文件打不开了，在网上找了一下资料，然后按照方法操作了一遍，好了，解决方法如下： 错误提示信息： An error has occurred.See error log for more details. Reason: com/genuitec/
  • 用正则删除文本中的html标签 adminjun javahtml正则表达式去掉html标签
    使用文本编辑器录入文章存入数据中的文本是HTML标签格式，由于业务需要对HTML标签进行去除只保留纯净的文本内容，于是乎Java实现自动过滤。 如下： public static String Html2Text(String inputString) { String htmlStr = inputString; // 含html标签的字符串 String textSt
  • 嵌入式系统设计中常用总线和接口 aijuans linux 基础
                   嵌入式系统设计中常用总线和接口         任何一个微处理器都要与一定数量的部件和外围设备连接，但如果将各部件和每一种外围设备都分别用一组线路与CPU直接连接，那么连线
  • Java函数调用方式——按值传递 ayaoxinchao java按值传递对象基础数据类型
    Java使用按值传递的函数调用方式，这往往使我感到迷惑。因为在基础数据类型和对象的传递上，我就会纠结于到底是按值传递，还是按引用传递。其实经过学习，Java在任何地方，都一直发挥着按值传递的本色。   首先，让我们看一看基础数据类型是如何按值传递的。   public static void main(String[] args) { int a = 2;
  • ios音量线性下降 bewithme ios音量
    直接上代码吧   //second 几秒内下降为0 - (void)reduceVolume:(int)second { KGVoicePlayer *player = [KGVoicePlayer defaultPlayer]; if (!_flag) { _tempVolume = player.volume;
  • 与其怨它不如爱它 bijian1013 选择理想职业规划
            抱怨工作是年轻人的常态，但爱工作才是积极的心态，与其怨它不如爱它。         一般来说，在公司干了一两年后，不少年轻人容易产生怨言，除了具体的埋怨公司“扭门”，埋怨上司无能以外，也有许多人是因为根本不爱自已的那份工作，工作完全成了谋生的手段，跟自已的性格、专业、爱好都相差甚远。  
  • 一边时间不够用一边浪费时间 bingyingao 工作时间浪费
    一方面感觉时间严重不够用，另一方面又在不停的浪费时间。 每一个周末，晚上熬夜看电影到凌晨一点，早上起不来一直睡到10点钟，10点钟起床，吃饭后玩手机到下午一点。 精神还是很差，下午像一直野鬼在城市里晃荡。 为何不尝试晚上10点钟就睡，早上7点就起，时间完全是一样的，把看电影的时间换到早上，精神好，气色好，一天好状态。 控制让自己周末早睡早起，你就成功了一半。 有多少个工作
  • 【Scala八】Scala核心二：隐式转换 bit1129 scala
    Implicits work like this: if you call a method on a Scala object, and the Scala compiler does not see a definition for that method in the class definition for that object, the compiler will try to con
  • sudoku slover in Haskell (2) bookjovi haskellsudoku
    继续精简haskell版的sudoku程序，稍微改了一下，这次用了8行，同时性能也提高了很多，对每个空格的所有解不是通过尝试算出来的，而是直接得出。   board = [0,3,4,1,7,0,5,0,0, 0,6,0,0,0,8,3,0,1, 7,0,0,3,0,0,0,0,6, 5,0,0,6,4,0,8,0,7,
  • Java-Collections Framework学习与总结-HashSet和LinkedHashSet BrokenDreams linkedhashset
            本篇总结一下两个常用的集合类HashSet和LinkedHashSet。         它们都实现了相同接口java.util.Set。Set表示一种元素无序且不可重复的集合；之前总结过的java.util.List表示一种元素可重复且有序
  • 读《研磨设计模式》-代码笔记-备忘录模式-Memento bylijinnan java设计模式
    声明： 本文只为方便我个人查阅和理解，详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/ import java.util.ArrayList; import java.util.List; /* * 备忘录模式的功能是，在不破坏封装性的前提下，捕获一个对象的内部状态，并在对象之外保存这个状态，为以后的状态恢复作“备忘”
  • 《RAW格式照片处理专业技法》笔记 cherishLC PS
    注意，这不是教程！仅记录楼主之前不太了解的 一、色彩（空间）管理 作者建议采用ProRGB（色域最广），但camera raw中设为ProRGB，而PS中则在ProRGB的基础上，将gamma值设为了1.8（更符合人眼） 注意：bridge、camera raw怎么设置显示、输出的颜色都是正确的（会读取文件内的颜色配置文件），但用PS输出jpg文件时，必须先用Edit->conv
  • 使用 Git 下载 Spring 源码 编译 for Eclipse crabdave eclipse
    使用 Git 下载 Spring 源码 编译 for Eclipse   1、安装gradle，下载 http://www.gradle.org/downloads 配置环境变量GRADLE_HOME，配置PATH  %GRADLE_HOME%/bin，cmd，gradle -v   2、spring4 用jdk8 下载 https://jdk8.java.
  • mysql连接拒绝问题 daizj mysql登录权限
    mysql中在其它机器连接mysql服务器时报错问题汇总 一、[running][email protected]:~$mysql -uroot -h 192.168.9.108 -p   //带-p参数，在下一步进行密码输入 Enter password:    //无字符串输入 ERROR 1045 (28000): Access
  • Google Chrome 为何打压 H.264 dsjt applehtml5chromeGoogle
    Google 今天在 Chromium 官方博客宣布由于 H.264 编解码器并非开放标准，Chrome 将在几个月后正式停止对 H.264 视频解码的支持，全面采用开放的 WebM 和 Theora 格式。 Google 在博客上表示，自从 WebM 视频编解码器推出以后，在性能、厂商支持以及独立性方面已经取得了很大的进步，为了与 Chromium 现有支持的編解码器保持一致，Chrome
  • yii 获取控制器名 和方法名 dcj3sjt126com yiiframework
    1. 获取控制器名 在控制器中获取控制器名:  $name = $this->getId(); 在视图中获取控制器名:    $name = Yii::app()->controller->id;    2. 获取动作名  在控制器beforeAction()回调函数中获取动作名:  $name =
  • Android知识总结（二） come_for_dream android
    明天要考试了，速速总结如下   1、Activity的启动模式        standard：每次调用Activity的时候都创建一个（可以有多个相同的实例，也允许多个相同Activity叠加。）        singleTop：可以有多个实例，但是不允许多个相同Activity叠加。即，如果Ac
  • 高洛峰收徒第二期：寻找未来的“技术大牛” ——折腾一年，奖励20万元 gcq511120594 工作项目管理
    高洛峰，兄弟连IT教育合伙人、猿代码创始人、PHP培训第一人、《细说PHP》作者、软件开发工程师、《IT峰播》主创人、PHP讲师的鼻祖！ 首期现在的进程刚刚过半，徒弟们真的很棒，人品都没的说，团结互助，学习刻苦，工作认真积极，灵活上进。我几乎会把他们全部留下来，现在已有一多半安排了实际的工作，并取得了很好的成绩。等他们出徒之日，凭他们的能力一定能够拿到高薪，而且我还承诺过一个徒弟，当他拿到大学毕
  • linux expect heipark expect
    1. 创建、编辑文件go.sh   #!/usr/bin/expect spawn sudo su admin expect "*password*" { send "13456\r\n" } interact    2. 设置权限   chmod u+x go.sh  3.
  • Spring4.1新特性——静态资源处理增强 jinnianshilongnian spring 4.1
    目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
  • idea ubuntuxia 乱码 liyonghui160com
      1.首先需要在windows字体目录下或者其它地方找到simsun.ttf 这个 字体文件。 2.在ubuntu 下可以执行下面操作安装该字体： sudo mkdir /usr/share/fonts/truetype/simsun sudo cp simsun.ttf /usr/share/fonts/truetype/simsun fc-cache -f -v
  • 改良程序的11技巧 pda158 技巧
    有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点，程序你只写一次，但以后会无数次的阅读。当你第二天回头来看你的代码 时，你就要开始阅读它了。当你把代码拿给其他人看时，他必须阅读你的代码。因此，在编写时多花一点时间，你会在阅读它时节省大量的时间。   让我们看一些基本的编程技巧：   尽量保持方法简短 永远永远不要把同一个变量用于多个不同的
  • 300个涵盖IT各方面的免费资源（下）——工作与学习篇 shoothao 创业免费资源学习课程远程工作
    工作与生产效率:   A. 背景声音 Noisli:背景噪音与颜色生成器。 Noizio:环境声均衡器。 Defonic:世界上任何的声响都可混合成美丽的旋律。 Designers.mx:设计者为设计者所准备的播放列表。 Coffitivity:这里的声音就像咖啡馆里放的一样。 B. 避免注意力分散 Self Co
  • 深入浅出RPC uule rpc
    深入浅出RPC-浅出篇 深入浅出RPC-深入篇   RPC Remote Procedure Call Protocol 远程过程调用协议   它是一种通过网络从远程计算机程序上请求服务，而不需要了解底层网络技术的协议。RPC协议假定某些传输协议的存在，如TCP或UDP，为通信程序之间携带信息数据。在OSI网络通信模型中，RPC跨越了传输层和应用层。RPC使得开发
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他