前景背景样本不均衡解决方案:Focal Loss,GHM与PISA(附python实现代码)
参考文献:Imbalance Problems in Object Detection: A Review
1 定义
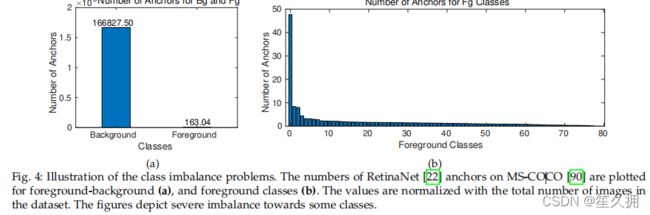
在前景-背景类别不平衡中,背景占有很大比例,而前景的比例过小,这类问题是不可避免的,因为大多数边界框都是由边界标记为背景(即否定)类框匹配和标签模块如图 4(a) 所示。一般来说,前景背景不均衡现象 出现在训练期间,它不依赖于数据集中每个类的样本的个数,因为但对于样本来说,它不包含前景和背景的任何相关信息。
2 解决方案
我们可以将前景背景类不平衡的解决方案分为四类:(i)硬采样方法,(ii)软抽样方法( Soft Sampling Methods),(iii)无抽样方法和(iv)生成方法。 每组方法在下面的小节中详细解释。在采样方法中,边界框(BBi)对损失函数的贡献(wi)调整为:wiCE( p ),这里CE代表的是cross-entropy loss。
硬采样和软采样方法在 wi 的可能值上有所不同。对于硬采样方法,wi ∈ {0, 1},即 BB 是要么被选中,要么被丢弃。 对于软采样方法,wi ∈ [0, 1],即样本的贡献调整为一个权重weight,每个 BB 都以不同的权重包含在训练过程中。
2.1 软抽样方法
软采样调整每个样本在训练过程中迭代的权重(wi),这与硬采样不同,没有样本被丢弃,整个数据集用于更新参数中。该方法同样也可以应用在分类任务中。
2.1.1 Focal Loss
推导:
 为了解决正负样本不均衡,乘以权重 α \alpha α:
为了解决正负样本不均衡,乘以权重 α \alpha α:

一般根据各类别数据占比,对 α \alpha α进行取值,即当class_1占比为30%时, α = 0.3 \alpha = 0.3 α=0.3,但是这个并不能解决所有问题。因为根据正负难易,样本一共可以分为以下四类:
| 难 | 易 | |
|---|---|---|
| 正 | 正难 | 正易 |
| 负 | 负难 | 负易 |
虽然 α \alpha α 平衡了正负样本,但对难易样本的不平衡没有任何帮助。其中易分样本(即,置信度高的样本)对模型的提升效果非常小,即模型无法从中学习大量的有效信息。所以模型应该主要关注于那些难分样本。(这个假设是有问题的,GHM对其进行了改进)。
我们希望模型能更关注容易错分的数据,反向思考,就是让模型别那么关注容易分类的样本。因此,Focal Loss的思路就是,把高置信度的样本损失降低

实验表明 γ \gamma γ 取2, α \alpha α 取0.25的时候效果最佳。
| 难 | 易 | |
|---|---|---|
| 正 | 正难 | 正易, γ \gamma γ衰减 |
| 负 | 负难, α \alpha α衰减 | 负易 , γ \gamma γ 与 α \alpha α 衰减 |
模型是如何通过 ( 1 − p ) γ (1-p)^{\gamma} (1−p)γ控制损失的衰减的呢?
当样本被误分类时,p很小, ( 1 − p ) γ (1-p)^{\gamma} (1−p)γ很大,loss不怎么受影响。当样本被正确分类,p很大, ( 1 − p ) γ (1-p)^{\gamma} (1−p)γ变小,loss衰减。
比如:当为1,p为0.9时,Focal Loss wei为![]()
这个容易分类的样本,损失和cross-entropy相比,衰减了100倍。
完整代码:
# 二分类
class BCEFocalLoss(torch.nn.Module):
"""
https://github.com/louis-she/focal-loss.pytorch/blob/master/focal_loss.py
二分类的Focalloss alpha 固定
"""
def __init__(self, gamma=2, alpha=0.25, reduction='sum'):
super().__init__()
self.gamma = gamma
self.alpha = alpha
self.reduction = reduction
def forward(self, preds, targets):
"preds:[B,C],targets:[B]"
pt = torch.sigmoid(preds)
pt = pt.clamp(min=0.0001,max = 1.0) # 概率过低,logpt后,loss返回nan
# 我在gpu上使用时,不加.to(targets.device),报错
targets = torch.zeros(targets.size(0),2).to(targets.device).scatter_(1,targets.view(-1,1),1)
loss = - self.alpha * (1 - pt) ** self.gamma * targets * torch.log(pt) - \
(1 - self.alpha) * pt ** self.gamma * (1 - targets) * torch.log(1 - pt)
if self.reduction == 'elementwise_mean':
loss = torch.mean(loss)
elif self.reduction == 'sum':
loss = torch.sum(loss)
return loss
# 多分类
class FocalLoss(nn.Module):
"""
Ref: https://github.com/yatengLG/Focal-Loss-Pytorch/blob/master/Focal_Loss.py
FL(pt) = -alpha_t(1-pt)^gamma log(pt)
alpha: 类别权重,常数时,类别权重为:[alpha,1-alpha,1-alpha,...];列表时,表示对应类别权重
gamma: 难易分类的样本权重,使得模型更关注难分类的样本
优点:帮助区分难分类的不均衡样本数据
"""
def __init__(self, num_classes, alpha=0.25,gamma=2,reduce=True):
super(FocalLoss,self).__init__()
self.num_classes = num_classes
self.gamma = gamma
self.reduce = reduce
if alpha is None:
self.alpha = torch.ones(self.num_classes,1)
else:
self.alpha = torch.zeros(num_classes)
self.alpha[0] = alpha
self.alpha[1:] += (1-alpha)
def forward(self,preds,targets):
"preds:[B,C],targets:[B]"
preds = preds.view(-1,preds.size(-1)) #[B,C]
self.alpha = self.alpha.to(preds.device)
logpt = F.log_softmax(preds,dim=1)
pt = F.softmax(preds).clamp(min=0.0001,max=1.0)
logpt = logpt.gather(1,targets.view(-1,1)) # 对应类别值
pt = pt.gather(1,targets.view(-1,1))
self.alpha = self.alpha.gather(0,targets.view(-1))
loss = -(1-pt) **self.gamma *logpt
loss = self.alpha*loss.t()
if self.reduce:
return loss.mean()
else:
return loss.sum()
2.1.2 Gradient Harmonizing Mechanism (GHM)
Focal Loss对容易分类的样本进行了损失衰减,让模型更关注难分样本,并通过 α \alpha α和 γ \gamma γ进行调参。这样相比CE loss 可以提高效果,但是也存在一些问题:
- Focal loss有两个超参数( α \alpha α和 γ \gamma γ),调整起来十分费力。
- Focal loss 是个静态loss,不会自适应于数据的分布,在训练的过程中会一直的变化。
GHM认为,类别不均衡可总结为难易分类样本的不均衡,而这种难分样本的不均衡又可视为梯度密度分布的不均衡。假设一个正样本被正确分类,它就是正易样本,损失不大,模型不能从中获益。而一个错误分类的样本,更能促进模型迭代。实际应用中,大量的样本都是属于容易分类的类型,这种样本一个起不了太大作用,但量级过大,在模型进行梯度更新时,起主要作用,使得模型朝这类数据更新
GHM中提到:
- 有一部分难分样本就是离群点,不应该给他太多关注;
- 样本不均衡的基本效果可以通过梯度密度直接统计得到,不需要调参。
简而言之:Focal Loss是从置信度p来调整loss,GHM通过一定范围置信度p的样本数来调整loss。

定义g:

代码表示为:
g = torch.abs(pred.sigmoid().detach() - target)
g的值表示样本的属性(easy/hard), 意味着对全局梯度的影响。尽管梯度的严格定义应该是在整个参数空间,但是g是样本梯度的成比例的norm,在这片论文中g被称作gradient norm。
不同属性的样本(hard/easy,pos/neg)可以由 gradient norm的分布来表示。在图1左中可以看出变化非常大。具有 小 gradient norm 的样本具有很大的密度,它们对应于大量的负样本(背景)。由于大量的简单负样本,我们使用log轴来显示样本的分数,以演示具有不同属性的样本的方差的细节。尽管一个easy样本在全局梯度上相比hard样本具有更小的贡献,但是大量的easy样本的全部贡献会压倒少数hard样本的贡献,所以训练过程变得无效。除此之外,论文还发现具有非常 大gradient norm的样本(very hard examples)的密度微大于中间样本的密度。并且发现这些very hard样本大多数是outliers,因为即使模型收敛它们始终稳定存在。如果收敛模型被强制学习分类这些outliers,对其他样本的分类可能不会那么的准确
根据gradient norm分布的分析,GHM关注于不同样本梯度贡献的协调。大量由easy样本产生的累积梯度可以被largely down-weighted并且outliers也可以被相对的down-weighted。最后,每种类型的样本分布将会使平衡的训练会更加的稳定和有效
| 小gradient norm样本 | 大gradient norm 样本 |
|---|---|
| 密度大 | 密度略大于 中间样本 |
| 大量背景 | outliers |
继续推导:
利用得到的g(gradient norm), 根据gradient density来协调处理。

其中: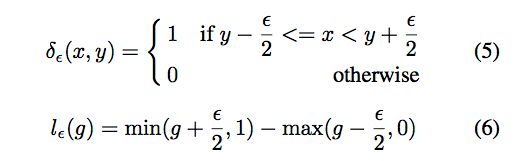
δ ε \delta_{\varepsilon} δε代表 在以g为中心长度为ϵ 的区域内的样本数量,并由区域的合理长度归一化(在下方代码中由于各个区间长度相同,没有做长度归一化,)
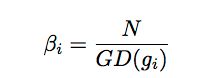
这里就代表各个样本权重。如果样本根据梯度是均匀分布的,GD(g)就为N,对于每个样本其权重相同:都为1。否则,具有大的密度的样本将会相对的降低权重。
最后,将GHM嵌入到分类损失中:将 β i \beta_{i} βi作为第i个样本的损失权重,损失函数的梯度密度的均衡形式为:
完整代码如下
def _expand_binary_labels(labels,label_weights,label_channels):
bin_labels = labels.new_full((labels.size(0), label_channels),0)
inds = torch.nonzero(labels>=1).squeeze()
if inds.numel() >0:
bin_labels[inds,labels[inds]] = 1
bin_label_weights = label_weights.view(-1,1).expand(label_weights.size(0),label_channels)
return bin_labels, bin_label_weights
class GHMC(nn.Module):
"""GHM Classification Loss.
Ref:https://github.com/libuyu/mmdetection/blob/master/mmdet/models/losses/ghm_loss.py
Details of the theorem can be viewed in the paper
"Gradient Harmonized Single-stage Detector".
https://arxiv.org/abs/1811.05181
Args:
bins (int): Number of the unit regions for distribution calculation.
momentum (float): The parameter for moving average.
use_sigmoid (bool): Can only be true for BCE based loss now.
loss_weight (float): The weight of the total GHM-C loss.
"""
def __init__(self, bins=10, momentum=0, use_sigmoid=True, loss_weight=1.0,alpha=None):
super(GHMC, self).__init__()
self.bins = bins
self.momentum = momentum
edges = torch.arange(bins + 1).float() / bins
self.register_buffer('edges', edges)
self.edges[-1] += 1e-6
if momentum > 0:
acc_sum = torch.zeros(bins)
self.register_buffer('acc_sum', acc_sum)
self.use_sigmoid = use_sigmoid
if not self.use_sigmoid:
raise NotImplementedError
self.loss_weight = loss_weight
self.label_weight = alpha
def forward(self, pred, target, label_weight =None, *args, **kwargs):
"""Calculate the GHM-C loss.
Args:
pred (float tensor of size [batch_num, class_num]):
The direct prediction of classification fc layer.
target (float tensor of size [batch_num, class_num]):
Binary class target for each sample.
label_weight (float tensor of size [batch_num, class_num]):
the value is 1 if the sample is valid and 0 if ignored.
Returns:
The gradient harmonized loss.
"""
# the target should be binary class label
# if pred.dim() != target.dim():
# target, label_weight = _expand_binary_labels(
# target, label_weight, pred.size(-1))
# 我的pred输入为[B,C],target输入为[B]
target = torch.zeros(target.size(0),2).to(target.device).scatter_(1,target.view(-1,1),1)
# 暂时不清楚这个label_weight输入形式,默认都为1
if label_weight is None:
label_weight = torch.ones([pred.size(0),pred.size(-1)]).to(target.device)
target, label_weight = target.float(), label_weight.float()
edges = self.edges
mmt = self.momentum
weights = torch.zeros_like(pred)
# gradient length
# sigmoid梯度计算
g = torch.abs(pred.sigmoid().detach() - target)
# 有效的label的位置
valid = label_weight > 0
# 有效的label的数量
tot = max(valid.float().sum().item(), 1.0)
n = 0 # n valid bins
for i in range(self.bins):
# 将对应的梯度值划分到对应的bin中, 0-1
inds = (g >= edges[i]) & (g < edges[i + 1]) & valid
# 该bin中存在多少个样本
num_in_bin = inds.sum().item()
if num_in_bin > 0:
if mmt > 0:
# moment计算num bin
self.acc_sum[i] = mmt * self.acc_sum[i] \
+ (1 - mmt) * num_in_bin
# 权重等于总数/num bin
weights[inds] = tot / self.acc_sum[i]
else:
weights[inds] = tot / num_in_bin
n += 1
if n > 0:
# scale系数
weights = weights / n
loss = F.binary_cross_entropy_with_logits(
pred, target, weights, reduction='sum') / tot
return loss * self.loss_weight
上图展示了不同损失的梯度norm,为了方便采用CE的原始梯度norm:g = ∣ p − p ∗ ∣ g=|p-p*|g=∣p−p∗∣,作为x轴因为密度是根据g计算的。可以看出FL与GHM-C具有相似的趋势,代表具有最佳参数的FL与均匀梯度协调很相似。但是GHM-C具有一个Focal loss忽视了的优点,降低了outliers的权重。
参考文献:
- 样本不均衡-Focal loss GHM,作者:第一个读书笔记
- Focal Loss 以及实现trick(附python实现代码)作者:Yao Yong
- 5分钟理解Focal Loss与GHM——解决样本不平衡利器 作者:中国移不动
2.1.3 PrIme Sample Attention (PISA)
PISA 方法和 Focal loss 和 GHM 出发点不一样, Focal loss 和 GHM 是利用 loss 来度量样本的难易分类程度,而本篇论文做者从 mAP 出发来度量样本的难易程度。
先介绍一下mAP:
P:precision,预测出的所有目标中正确的比例(true positives / true positives + false positives)
AP:average precision,每一类别P值的平均值
MAP:mean average precision,对所有类别的AP取均值
多标签图像分类任务中图片的标签不止一个,因此评价不能用普通单标签图像分类的标准,即mean accuracy,该任务采用的是和信息检索中类似的方法—mAP(mean Average Precision),虽然其字面意思和mean accuracy看起来差不多,但是计算方法要繁琐得多。
该作者提出改论文的方法考虑了两个方面:
-
样本之间不该是相互独立的或同等对待。基于区域的目标检测是从大量候选框中选取一小部分边界框,以覆盖图像中的全部目标。所以,不一样样本的选择是相互竞争的,而不是独立的。**通常来讲,检测器更可取的作法是在确保全部感兴趣的目标都被充分覆盖时,在每一个目标周围的边界框产生高分,而不是对全部正样本产生高分。**作者研究代表关注那些与gt目标有最高IOU的样本是实现这一目标的有效方法。
-
目标的分类和定位是有联系的。定位目标周围的样本很是重要,这一观察具备深入的意义,即目标的分类和定位密切相关。具体地,定位好的样本须要具备高置信度好的分类。
PISA由两个部分组成:
- 基于重要性的样本重加权(ISR)
- 分类感知回归损失(CARL)。
ISR(Importance-based Sample Reweighting)
ISR由正样本重加权和负样本重加权组成,分别表示为ISR-P和ISR-N。 对于阳性样本,我们采用IoU-HLR作为重要性度量;对于阴性样本,我们采用Score-HLR。 给定重要性度量,剩下的问题是如何将重要性映射到适当的损失权重。
IoU-HLR:
为了计算IoU-HLR,首先将所有样本根据其最近的gt目标划分为不同的组。接下来,使用与gt的IoU降序对每个组中的样本进行排序,并获得IoU局部排名(IoU-LR)。随后,以相同的IoU-LR采样并按降序对其进行排序。具体来说,收集并分类所有top1 IoU-LR样本,其次是top2,top3,依此类推。这两个步骤将对所有样本进行排序

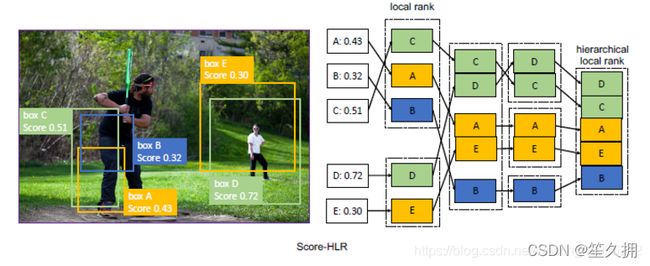
Score-HLR
以类似于IoU-HLR的方式计算负样本的Score-HLR。 与由每个gt目标自然分组的正样本不同,负样本也可能出现在背景区域,因此我们首先使用NMS将它们分组到不同的群集中。 将所有前景类别中的最高分数用作负样本的得分,然后执行与计算IoU-HLR相同的步骤。
未完…