9-1小波变换 小波分解和重构(matlab程序)

1.简述

      一、小波处理信号的一般过程
1）取样：这是一个预处理步骤。若信号连续，那么必须以能够捕获原信号必要细节的速率取样。不同的应用决定了不同的取样率。如：原信号的细节频率为20kHz，由Nyquist采样定理，此时的取样率至少应为细节频率的两倍，即40kHz，才能保证细节频率不失真。

2）分解：信号取样后，选择一个最高级近似系数f j ∈ v，以便能最佳的逼近f ff。之后，通过多分辨率分解算法，将信号进行逐级分解。该步骤的输出是各级别的小波系数（细节系数）和最低级别（或自定义的合适级别）的近似系数。该系数集就是下一步信号处理中要处理的对象。

3）信号处理：通过舍弃非显著系数可以压缩信号，或者以某种方式使信号滤波或去噪。该步骤的输出是修改过的系数集（细节系数集），可被存储或立即重构以重组经过处理的信号。但在某些情况下，原信号不再有用，可以舍弃，如：奇异性检测。

4）重构：把经过信号处理步骤修改过的系数集（细节系数集），应用多分辨率重构算法，进行逐级重构，该步骤输出最高级近似系数。

二、分解算法
1. 分解迭代
首先，基于取样率和进行什么样的多分辨率分析确定f ff的近似空间，其能最佳的反映f ff的各种信息。之后选择 ，以便能最佳的逼近f 。

三、重构算法
1. 重构迭代
一旦信号分解完毕，就可以通过修改某些w j ′ w_{j'}w ,实现对信号的处理。如果想要滤除信号中的噪声，那么f ff中的w j ′ w_{j'}w 中相应于不想要的频率部分可被舍弃，结果使得噪声被显著减小。如果想要对原信号进行数据压缩，可将幅值较小的w j ′ w_{j'}w 分量舍弃，这不会显著的改变原信号特征，但会获得极大的数据压缩效果。当w j ′ w_{j'}w 分量被修改完成之后，需要一个重构算法，重新组装被滤波或被压缩的信号，这个过程即为信号的重构.

2. 多分辨率重构算法
对近似系数和小波系数采用离散滤波器实现形式进行重构。

这几乎就是两个卷积之和，唯一区别是卷积的指标是k − l k-lk−l而不是k − 2 l k-2lk−2l，即上式是一个奇数(l ‾ ( k − ( 2 l + 1 ) ) \overline{l}_{(k-(2l+1))} 缺失的卷积。可以利用上取样算子简单地用0乘奇数项而复原回来。

形成一个在所有的奇数位置为0的新序列。原来的每个非零项给定一个新的偶数指标，这只要把原有的指标倍乘即可。

通过离散滤波器（卷积算子），来描述迭代步骤。

2.代码

load woman;             %打开显示原始的图像
imshow(X,map);          %X包含原始图像信息，map是调色板，这是一个索引图像
%% 对图像X数据信息进行单层分解，小波为db1
nbcol=size(map,1);
[cA1,cH1,cV1,cD1]=dwt2(X,'db1');   
cod_X=wcodemat(X,nbcol);
cod_cA1=wcodemat(cA1,nbcol);
cod_cH1=wcodemat(cH1,nbcol);
cod_cV1=wcodemat(cV1,nbcol);
cod_cD1=wcodemat(cD1,nbcol);
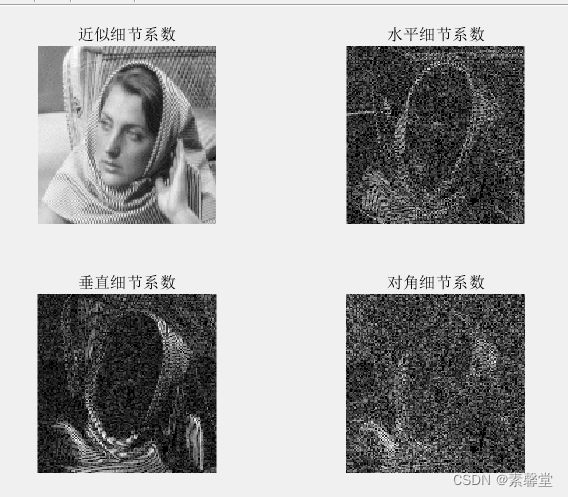
%%   图像编码    4种细节系数
figure
subplot(221)
imshow(cod_cA1,map)
title('近似细节系数')
subplot(222)
imshow(cod_cH1,map)
title('水平细节系数')
subplot(223)
imshow(cod_cV1,map)
title('垂直细节系数')
subplot(224)
imshow(cod_cD1,map)
title('对角细节系数')
Y=idwt2(cA1,cH1,cV1,cD1,'db1','nbcol');
%%   对分解的细节系数执行单层重构，小波为db1
figure;
imshow(Y,map);
title('重构后的图像')
 

3.运行结果