ACL2023 - An AMR-based Link Prediction Approach for Document-level Event Argument Extraction
An AMR-based Link Prediction Approach for Document-level Event Argument Extraction
论文:https://arxiv.org/abs/2305.19162
代码:https://github.com/ayyyq/TARA
期刊/会议:ACL 2023
摘要
最近的工作引入了用于文档级事件论元提取(文档级EAE)的抽象语义表示(AMR),因为AMR提供了对复杂语义结构的有用解释,并有助于捕获长距离依赖关系。然而,在这些工作中,AMR仅隐含地使用,作为附加特征或训练信号。由于所有的事件结构都可以从AMR中推断出来,这项工作将EAE重新表述为AMR图上的链接预测问题。
由于AMR是一种通用结构,并不完全适合EAE,我们提出了一种新的图结构,即定制AMR图(Tailored AMR Graph, TAG),它压缩信息量较小的子图和边缘类型,集成跨度信息,并突出显示同一文档中的周围事件。利用TAG,我们进一步提出了一种新的方法,使用图神经网络作为链接预测模型来查找事件论元。
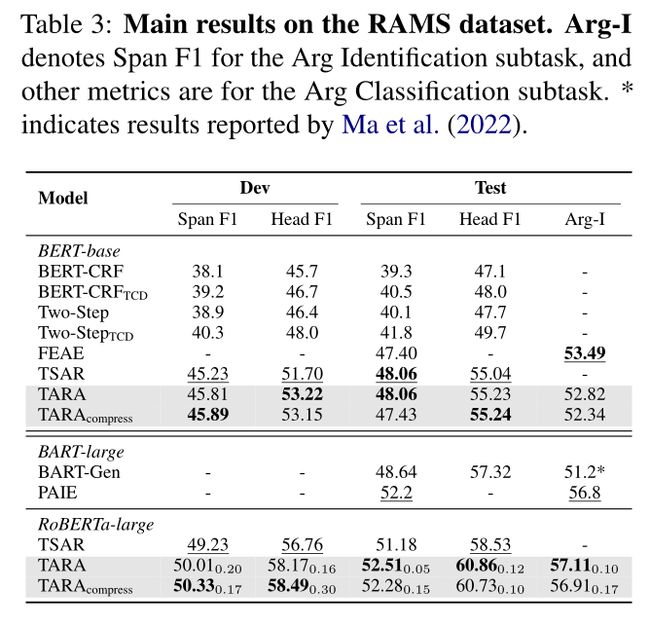
我们在WikiEvents和RAMS上进行的大量实验表明,这种更简单的方法分别比最先进的模型高3.63pt和2.33pt F1,并减少了56%的推理时间。
1、简介
先前的工作通过强化神经序列模型隐式地使用AMR信息,而不是显式地使用离散结构。离散AMR结构可以迫使模型更好地关注谓词论元结构和与EAE最相关的内容,因此比隐式AMR具有更强的效果。
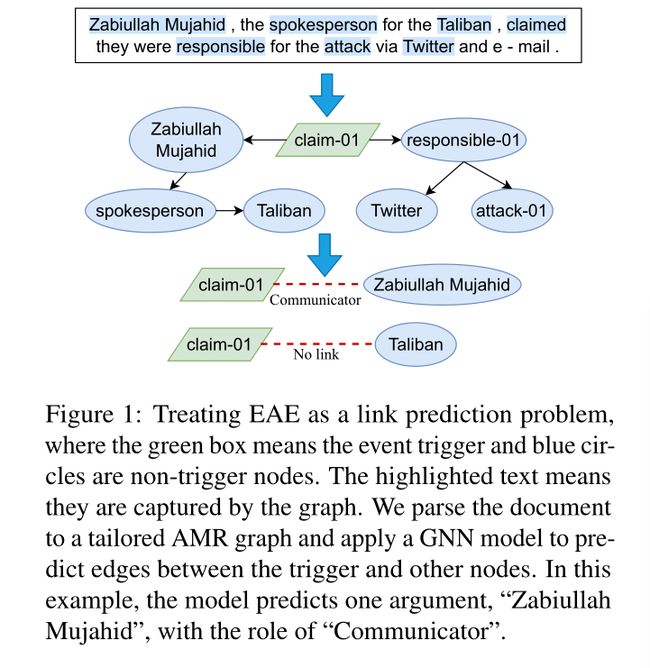
我们的目标是通过将EAE转化为链路预测任务,利用显式AMR的潜力来改进EAE,图1说明了该框架。我们将输入文档解析为图结构,并采用链接预测模型来查找事件论元。我们通过一个节点是否连接到触发词节点来确定它是否是一个论元。将EAE公式化为链接预测问题的优点有三方面:1)AMR图通常比原始文本更紧凑(见第2.2节),因此处理AMR以查找论元将是简单有效的。2) 多个论元和事件之间的依赖关系被明确地捕获,而之前的工作(Liao and Grishman,2010;Du et al,2022)已经指出了这些依赖关系的重要性,这些依赖关系仅在特征空间中被隐含地考虑。3) 正如我们的实验所示,更简单的模型架构和稀疏图可以提高效率(最多节省56%的推理时间)。
所提出的方法假设AMR图包含EAE的所有必要信息。然而,由于现成的AMR解析器生成的原始AMR图不满足这一假设。首先,它们只覆盖了WikiEvents中72.2%的事件论元,阻碍了EAE模型直接在解析的AMR图上的性能。主要问题是AMR图是在单词级别定义的,但事件论元可能是文本跨度。其次,最先进的AMR解析器的Smatch分数约为85(Bai et al. 2022),这也会导致信息丢失。为了解决上述问题,我们提出了一种新的定制AMR图(TAG),它压缩与EAE无关的信息,通过跨度建议模块将单词合并到文本跨度中,并突出显示同一文档中的周围事件,以鼓励他们的交流。特别是,TAG中的节点数量大约相当于WikiEvents中单词的47%,这是一个显著的减少。由于过多的分散注意力的信息是文档级任务的一个主要挑战,我们还期望通过关注TAG来提高性能,我们的实验结果证明了这一点。如果跨度建议模块增加了足够的文本跨度,TAG可以覆盖所有EAE样本,我们将在附录-A.3中讨论跨度召回和模型效率之间的权衡。
尽管链接预测模型有很大的设计空间,但我们选择了一种简单的架构,将GNN层堆叠在预训练的文本编码器之上。整个模型被称为TARA,用于基于定制AMR的论元提取。我们在最新的文档级EAE数据集WikiEvents(Li et al,2021)和RAMS(Ebner et al,2020)上进行了广泛的实验。TARA分别比SOTA提高了3.63pt和2.33pt。由于GNN中的交互是稀疏的,因此我们的模型的计算成本也更低,节省了高达56%的推理时间。
据我们所知,我们是第一个将EAE转化为AMR图上的链接预测问题的人。
2、方法
在本节中,我们首先解释了如何将EAE转化为链路预测问题,并讨论了这样做的好处(第2.1节)。为了使AMR图更好地适应EAE任务并确保公式化是无损失的,我们对AMR图进行了一系列修改,生成了一个紧凑且信息丰富的图,称为Tailored AMR图(TAG)(第2.2节)。
2.1 EAE作为链路预测问题
形式上,给定文档 D \mathbf{D} D和事件类型为 e e e的事件触发词 τ \tau τ,文档级EAE的目标是提取一组与 τ \tau τ相关的事件论元 A \mathbf{A} A。我们将EAE转化为链路预测问题,该问题是在TAG上定义的。假设TAG中的所有节点都与输入序列中的文本跨度对齐,在图中捕获触发词和论元,并标记与事件触发词对应的节点(我们将在第2.2节中讨论如何满足这些条件)。
因此,我们将链接预测模型应用于文档 D \mathbf{D} D的定制AMR图 G t \mathcal{G}_t Gt。如果该模型预测存在连接节点 u u u和事件触发词 τ \tau τ的类型为 r r r的边,则我们说 u u u的相应文本跨度是一个论元,并且它在具有触发词 τ \tau τ的事件中起到 r r r的作用。我们在图1中说明了这一过程,它还显示了定制的AMR图删除了输入文本中大量分散注意力的信息。请注意,删除的文本参与构建初始节点表示,因此模型仍然可以作为上下文访问它们的信息。详细实施见第2.3节。
2.2 为EAE定制AMR图
TAG可以建立在现成的AMR解析器生成的原始的AMR图上(Bai et al, 2022; Astudillo et al, 2020),该解析器还提供节点和单词之间的对齐信息。如上所述,原始的AMR图不足以解决EAE,因此我们通过压缩膨胀的子图来清理图,用跨度建议模块导出的跨度边界信息丰富图,并突出周围的事件以鼓励多个事件之间的交互。
**聚集边缘(Coalescing edges)**我们遵循先前的工作(ang and Ji, 2021; Xu et al, 2022),将细粒度AMR边缘类型聚类为表1所示的主要类别,并在完全连接所有句子的根节点之前逐句解析文档。
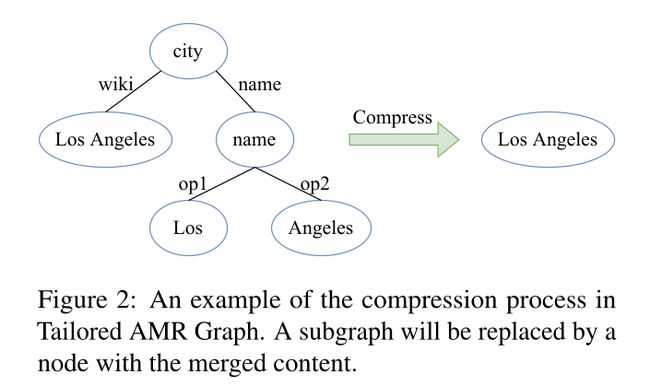
**压缩子图(Compressing Subgraphs)**AMR是严格的,并尽量反映所有细节。例如,图2显示了一个普通的AMR图使用五个节点来表示一个实体“Los Angeles”。由于EAE不需要这样详细的信息,我们可以将子图压缩到单个节点。我们发现,大约36%的节点和37%的边可以通过压缩来去除。注意,要压缩的子图的所有传入和传出边都将被继承,这样压缩就不会影响图的其余部分。流线型图不仅提高了效率和节省了内存,而且还促进了GNN的训练,因为更大的图通常需要更深的GNN。压缩过程只依赖于普通的AMR图,因此对于每个样本来说都是一次性开销。详细的压缩规则见附录B。
**缺失片段(Missing Spans)**普通的AMR图无法覆盖跨度形式的论元,因为它是在单词级别定义的,这损害了20%以上EAE样本的性能。为了克服这个问题,我们将跨度建议模块生成的跨度信息 S S S添加到 G t \mathcal{G}_t Gt中,如图3所示。我们遵循Zhang和Ji(2021)中介绍的想法,将生成的跨度与现有AMR节点合并。如果生成的跨度根据对齐信息与节点在文本序列中的位置完全匹配,我们会在节点的初始表示中添加一个特殊的节点类型嵌入,这样模型就可以知道跨度建议模块宣布了这个节点。如果生成的跨度与节点部分匹配,我们添加一个新节点来表示该跨度,并从部分匹配的节点继承连接词。我们还在这个节点和新节点之间添加了一条特殊的边,以指示它们的重叠。如果生成的跨度与任何现有节点都不匹配,我们添加一个新节点,并用一条特殊的边将其连接到其左侧和右侧最近的节点。
**周围的事件(Surrounding Events)**文档中的事件不是孤立的。最近的一项工作(Du et al, 2022)用包含其他事件的文本来增强输入,但AMR图的使用提供了一个更简单的解决方案。我们添加节点类型嵌入来指示节点是同一文档中的当前触发词或周围事件触发词。这种修改鼓励多个事件结构之间的通信,并且事件结构间的一致性可以帮助提取尽可能多的正确论元。例如,在同一份文件中,Attack事件的Victim很可能是Die事件的Victim,而不太可能是ChargeIndict事件的Defendant。
2.3 实施
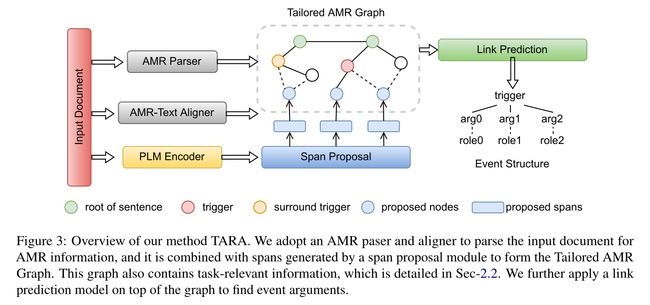
我们提出了一个新的模型来发现基于TAG的事件论元,图3概述了我们的方法。我们首先使用AMR解析器和对齐器解析输入文档,以获得普通的AMR图,如第2.2节所述,合并边并压缩子图以对其进行预处理。然后,我们用跨度建议模块生成的跨度来丰富图。接下来,我们使用预训练的文本编码器输出的token级特征来根据对齐信息初始化节点表示。最后,将基于GNN的链接预测模型应用于事件论元的预测。
编码器模块:给定输入文档 D = { w 1 , w 2 , … , w n } \mathbf{D}=\{w_1,w_2,\ldots,w_n\} D={w1,w2,…,wn},我们首先使用预训练的语言模型(例如BERT或RoBERTa)来获得每个单词 w i w_i wi的上下文表示 h i h_i hi:
H = [ h 1 , h 2 , … , h n ] = P L M ( [ w 1 , w 2 , … , w n ] ) H=[h_1,h_2,\ldots,h_n]=PLM([w_1,w_2,\ldots,w_n]) H=[h1,h2,…,hn]=PLM([w1,w2,…,wn])
对于范围从 w i w_i wi到 w j w_j wj的文本跨度 s i j s_{ij} sij,我们遵循Xu等人(2022),通过连接开始表示 h i h_i hi、结束表示 h j h_j hj和跨度的隐藏状态的平均池来计算其上下文表示 x s i j x_{s_ij} xsij,这将注入跨度边界信息。正式地
x s i j = W 0 [ W 1 h i ; W 2 h j ; 1 j − i + 1 ∑ t = i j h t ] x_{s_{ij}}=W_0[W_1h_i;W_2h_j;\frac{1}{j-i+1}\sum_{t=i}^{j} h_t] xsij=W0[W1hi;W2hj;j−i+11t=i∑jht]
其中, W 0 , W 1 , W 2 W_0,W_1,W_2 W0,W1,W2表示可训练参数。
跨度建议模块:为了找到尽可能多的论元,我们列举了长度为 m m m的所有跨度。根据Zaporojets等人(2022),我们应用一个简单的跨度建议步骤,根据前馈神经网络(FFNN)的跨度得分 Φ ( s ) \Phi(s) Φ(s),仅保留前 k k k个跨度:
Φ ( s ) = FFNN ( x s ) \Phi (s) =\text{FFNN} (x_s) Φ(s)=FFNN(xs)
然后,生成的 k k k个候选跨度(最有可能被称为论元跨度)将插入AMR图 G \mathcal{G} G,以构建我们提出的定制AMR图 G t \mathcal{G}_t Gt。我们分析了附录A.3中 k k k的选择对召回和效率的影响。
我们还最小化以下二分类交叉熵损失来训练论元识别:
L s p a n = − ( y log ( Φ ( x ) ) + ( 1 − y ) log ( 1 − Φ ( x ) ) ) L_{span}=-(y \log (\Phi(x))+(1-y) \log (1-\Phi(x))) Lspan=−(ylog(Φ(x))+(1−y)log(1−Φ(x)))
其中,当对应跨度的偏移量与标准论元跨度匹配时, y y y被分配为真标签,否则为假标签。
AMR图模块:如第2.2节所述, G t \mathcal{G}_t Gt中每个节点 u s u_s us的嵌入由对齐的跨度表示 x s x_s xs及其类型嵌入初始化:
g u s 0 = LayerNorm ( x s , T n o d e ( u s ) ) g_{u_s}^0=\text{LayerNorm}(x_s,\mathcal{T}_{node}(u_s)) gus0=LayerNorm(xs,Tnode(us))
T \mathcal{T} T是节点类型的查找表,包括 { t r i g g e r , s u r r o u n d i n g t r i g g e r , c a n d i d a t e s p a n , o t h e r } \{trigger,surrounding \ trigger,candidate\ span, other \} {trigger,surrounding trigger,candidate span,other}四种类型。新插入的节点通过新的边类型上下文连接到它们的相邻节点,这些节点在文本序列中很接近。
我们使用 L L L层堆叠的R-GCN(Schlichtkrull et al, 2018)通过具有不同关系类型的边来对不同节点之间的相互作用进行建模。第 l + 1 l+1 l+1层中节点的隐藏状态可以公式化为:
g u l + 1 = Relu ( W 0 ( l ) g u ( l ) + ∑ r ∈ R ∑ v ∈ N u r 1 c u , r W r ( l ) g v ( l ) ) g_u^{l+1}=\text{Relu}(W_0^{(l)}g_u^{(l)} +\sum_{r \in R} \sum_{v \in N_u^r} \frac{1}{c_{u,r}}W_r^{(l)}g_v^{(l)}) gul+1=Relu(W0(l)gu(l)+r∈R∑v∈Nur∑cu,r1Wr(l)gv(l))
其中, R R R是表1中AMR关系类型的簇, N u r N^r_u Nur表示在关系 r ∈ R r \in R r∈R和节点 u u u的邻居节点集, c u , r c_{u,r} cu,r是归一化常数。其中 W 0 ( l ) , W r ( l ) W_0^{(l)},W_r^{(l)} W0(l),Wr(l)是可训练的参数。
我们连接所有层的隐藏状态,并导出最终的节点表示 g u = W g [ g u 0 ; g u 1 ; … , g u L ] g_u=W_g[g^0_u;g^1_u;\ldots,g^L_u] gu=Wg[gu0;gu1;…,guL]。
分类模块:我们执行多类别分类来预测候选跨度扮演的角色,或者它不作为一个论元。如第2.1节所述,我们采用节点表示 g u s g_{u_s} gus和 g u τ g_{u_{\tau}} guτ,它们分别表示对齐的候选跨度 s s s和触发词 τ \tau τ。继Xu等人(2022)之后,我们还连接了事件类型嵌入。最终的分类表示可以公式化为:
z s = [ g u s ; g u τ ; T e v e n t ( e ) ] z_s=[g_{u_s};g_{u_{\tau}};\mathcal{T}_{event}(e)] zs=[gus;guτ;Tevent(e)]
最终,采用交叉熵损失函数:
L c = − ∑ s y s log P ( r ^ s = r s ) L_c=- \sum_{s} y_s \log P(\hat r_s=r_s) Lc=−s∑yslogP(r^s=rs)
r ^ s \hat r_s r^s是由 z s z_s zs上的FFNN获得的分数,并且 r s r_s rs是跨度 s s s的正确论元作用。
我们使用具有超参数 λ λ λ的多任务损失函数 L = L c + λ L s L=L_c+λL_s L=Lc+λLs来训练模型。因此,论元识别可以对论元分类产生积极影响。
3、实验
4、总结
我们提出在定制的AMR图上,将文档级事件论元抽取重新表述为链接预测问题。通过添加缺失的跨度、标记周围事件和消除噪声,AMR图针对EAE任务进行了定制。我们还介绍了一个基于TAG的链路预测模型来实现EAE。详细的实验表明,显式使用AMR图有利于论元提取。
更多论文解读