力扣 1 至 100 中等

欢迎访问我的博客首页。

---

1. LeetCode 2.两数相加

---

  题目。
  分析：因为是两个整数，且按逆序储存，所以题目比较简单，只需遍历链表即可。注意考虑 4 种情况：

class Solution {
public:
	ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
		if (l1 == nullptr)
			return l2;
		if (l2 == nullptr)
			return l1;

		ListNode *res = nullptr, *work = nullptr;
		int sum, carry = 0;
		// 1.链表l1和链表l2都没结束。
		while (l1 != nullptr && l2 != nullptr) {
			sum = l1->val + l2->val + carry;
			carry = sum / 10;
			sum = sum % 10;
			if (res == nullptr) {
				res = new ListNode(sum);
				work = res;
			}
			else {
				work->next = new ListNode(sum);
				work = work->next;
			}
			l1 = l1->next;
			l2 = l2->next;
		}
		// 2.链表l2结束。
		while (l1 != nullptr) {
			sum = l1->val + carry;
			carry = sum / 10;
			sum = sum % 10;
			work->next = new ListNode(sum);
			work = work->next;
			l1 = l1->next;
		}
		// 3.链表l1结束。
		while (l2 != nullptr) {
			sum = l2->val + carry;
			carry = sum / 10;
			sum = sum % 10;
			work->next = new ListNode(sum);
			work = work->next;
			l2 = l2->next;
		}
		// 4.链表l1和链表l2都结束，检查进位是否为0。
		if (carry != 0) {
			work->next = new ListNode(carry);
			work = work->next;
		}
		return res;
	}
};

  性能：时间复杂度是 $O(max(m+n))$，空间复杂度 $O(1)$。

2. LeetCode 3.无重复字符的最长子串

---

  详细内容在这里。

3. LeetCode 5.最长回文子串

---

  题目：给你一个字符串 s，找到 s 中最长的回文子串。牛客只求长度。相关题目《LeetCode 132.分割回文串Ⅱ》。
  分析：最长回文子串有时间复杂度为 $O(n^3)$、$O(n^2)$、$O(n)$ 的 3 类算法。时间复杂度为 $O(n^3)$ 的算法使用两层循环获取子串 s[i: j]，再使用一层循环判断 s[i: j] 是否为回文字符串。时间复杂度为 $O(n^2)$ 的算法有中心扩散法和动态规划法。时间复杂度为 $O(n)$ 的算法有 Manacher 算法，这个算法太复杂，这里不讨论。
  中心扩散法：遍历字符串中的每个字符 c，求以 c 为中心的回文字串长度。注意以 c 为中心的回文子串有 “aca” 和 “acca” 两种形式。

class Solution {
public:
	string longestPalindrome(string str) {
		if (str.size() < 2)
			return str;

		string res = str.substr(0, 1);
		for (int i = 0; i < str.size(); i++) {
			// 1.以str[i]为中心。
			string res1 = find(str, i - 1, i + 1);
			res = res.size() >= res1.size() ? res : res1;
			// 2.以str[i]str[i+1]为中心。
			if (str[i] == str[i + 1]) {
				string res2 = find(str, i - 1, i + 2);
				res = res.size() >= res2.size() ? res : res2;
			}
		}
		return res;
	}
private:
	string find(string& str, int left, int right) {
		while (true) {
			if (left < 0 || right >= str.size())
				break;
			if (str[left] == str[right]) {
				left--;
				right++;
			}
			else
				break;
		}
		return str.substr(left + 1, right - left - 1);
	}
};

  性能：第 1 个字符最多需要 0 次判断，第 2 个字符最多需要 1 次判断，…，第 n/2 个字符最多需要 (n/2)-1 次判断，所以最多需要 $2\times (0+1+\cdots +n/2-1)=n^2÷2$ 次判断，所以时间复杂度是 $O(n^2)$。因为使用了临时空间存放结果， 所以空间复杂度是 $O(n)$。如果使用两个数表示回文子串而不是使用临时空间 temp，空间复杂度就可以变为 $O(1)$。

  下面使用动态规划算法。

class Solution {
public:
	string longestPalindrome(string& str) {
		if (str.size() < 2)
			return str;

		int N = str.size(), begin = 0, maxlen = 1;
		vector<vector<int>> dp(N, vector<int>(N));
		// 1.长度为1的回文子串。
		for (int i = 0; i < N; i++)
			dp[i][i] = 1;
		// 2.长度大于等于3的回文子串。
		for (int len = 2; len <= N; len++) {
			for (int start = 0; start + len <= N; start++) {
				int end = start + len - 1;
				// 3.str[start]与str[end]不相等。
				if (str[start] != str[end])
					continue;
				// 4.str[start+1:end-1]不是回文字符串。
				if (dp[start + 1][end - 1] != end - start - 1)
					continue;
				// 5.str[start]与str[end]相等且str[start+1:end-1]是回文字符串。
				dp[start][end] = dp[start + 1][end - 1] + 2;
				if (dp[start][end] > maxlen) {
					maxlen = dp[start][end];
					begin = start;
				}
			}
		}
		return str.substr(begin, maxlen);
	}
};

  为了保证 end-1>= start+1，即 start+len-1>=start+1，我们让 len 从 2 开始递增。于是我们要给出最小问题 len=1 的解。上面的动态规划算法中，第一层循环让回文子串的长度递增，第二层循环让回文子串的起始位置递增。总之要保证先处理的问题比后处理的问题的规模更小。
  该题说明在设计动态规划算法时，一点要理清问题的增长方向，才能知道循环怎么写。一般的动态规划问题中，循环都是从小到大的，本题的两个循环都从小到大是不行的。
  本题还有另一种更好理解地划分问题的方法，代码如下。

class Solution {
public:
	string longestPalindrome(string& str) {
		if (str.size() < 2)
			return str;

		int N = str.size(), begin = 0, maxlen = 1;
		vector<vector<int>> dp(N, vector<int>(N));
		for (int start = N - 1; start >= 0; start--) {
			for (int end = start; end < N; end++) {
				if (start == end)
					dp[start][end] = 1;
				else if (str[start] == str[end] && dp[start + 1][end - 1] == end - start - 1)
					dp[start][end] = dp[start + 1][end - 1] + 2;
				if (dp[start][end] > maxlen) {
					maxlen = dp[start][end];
					begin = start;
				}
			}
		}
		return str.substr(begin, maxlen);
	}
};

4. LeetCode 6.Z 字形变换

---

  题目。将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

$$图4.1Z字形变换$$

  分析：我们把一竖列和后面斜向上的部分分为一组，如图 4.1，相连的一条竖直红线和一条斜线经过的元素称为一组。显然一组的元素个数最多是 $lenGroups=2\times numRows-2$，一共有 numGroups = ceil(1.0 * s.size() / lenGroups) 个这样的组。
  还可以发现，每组其实包含两列。在每组中，除了第一行和最后一行外，每行最多有两个元素：第一个元素在原数组中的下标是 $lenGroups\times x+y$；第二个元素在原数组中的下标是 $lenGroups\times (x+1)-y$。其中 x 是从 0 开始的行数的下标，y 是从 0 开始的组数的下标。这样我们就确定了转换后每行每列的元素。

class Solution {
public:
	string convert(string s, int numRows) {
		if (s.size() == 0 || numRows <= 0)
			return "";
		// 1.如果numRows为1，下面会出现除0的情况。
		if (numRows == 1)
			return s;
		// 2.numRows大于1。
		string res = "";
		int lenGroups = 2 * numRows - 2;
		int numGroups = ceil(1.0 * s.size() / lenGroups);
		for (int y = 0; y < numRows; y++) {
			for (int x = 0; x < numGroups; x++) {
				// 2.1竖直向下的元素。
				int index1 = lenGroups * x + y;
				if (index1 >= s.size())
					continue;
				res.push_back(s[index1]);
				// 2.2斜向上的元素。
				if (y > 0 && y < numRows - 1) {
					int index2 = lenGroups * (x + 1) - y;
					if (index2 >= s.size())
						continue;
					res.push_back(s[index2]);
				}
			}
		}
		return res;
	}
};

  分析：时间复杂度是 $O(n)$，空间复杂度是 $O(1)$。

5. LeetCode 8.字符串转换整数

---

  题目：输入的字符串形式是：(0 或多个空格，0 或 1 个正负号，0 或多个数字字符，0 或多个非数字字符)。
  注意：遇到非数字字符就停止解析。

class Solution {
public:
	int myAtoi(string s) {
		if (s.size() == 0)
			return 0;
		// 1.获取符号和第一个数字的下标。
		bool positive = true;
		int start = -1, end;
		for (int i = 0; i < s.size(); i++) {
			if (s[i] == '-' || s[i] == '+') {
				if (s[i] == '-')
					positive = false;
				if (i == s.size() - 1 || s[i + 1]<'0' || s[i + 1]>'9')
					return 0;
				start = i + 1;
				break;
			}
			// 找到第一个数字。
			else if (s[i] >= '0' && s[i] <= '9') {
				start = i;
				break;
			}
			// 遇到非空格字符就停止解析。
			else if (s[i] != ' ')
				return 0;
		}
		if (start == -1)
			return 0;
		// 2.获取最后一个数字的下标。
		end = start;
		while (end < s.size() && s[end] >= '0' && s[end] <= '9') {
			end++;
		}
		// 3.获取有效的数字部分。
		s = s.substr(start, end - start);
		// 4.存放结果。
		int sum = 0;
		int len = s.size();
		// 5.处理正数。
		int max = INT_MAX;
		if (positive == true) {
			for (int i = len - 1; i >= 0; i--) {
				if (s[i] == '0')
					continue;
				int exponent = len - 1 - i;
				if (exponent > 9)
					return INT_MAX;
				if (exponent == 9 && s[i] > '2')
					return INT_MAX;
				int numi = (s[i] - '0') * pow(10, exponent);
				if (numi >= INT_MAX - sum)
					return INT_MAX;
				sum += numi;
			}
			return sum;
		}
		// 6.处理负数。
		else {
			for (int i = len - 1; i >= 0; i--) {
				if (s[i] == '0')
					continue;
				int exponent = len - 1 - i;
				if (exponent > 9)
					return INT_MIN;
				if (exponent == 9 && s[i] > '2')
					return INT_MIN;
				int numi = (s[i] - '0') * pow(10, exponent);
				if (numi - 1 >= INT_MAX - sum) // 注意这里是INT_MAX而不是INT_MIN。
					return INT_MIN;
				sum += numi;
			}
			return -1 * sum;
		}
	}
};

  处理越界问题：INT_MAX = 2147483647，INT_MIN = -2147483648，最高位是 2 乘 10 的 9 次方。因为这两个边界的绝对值不相同，所以我们分开讨论，如第 5 部分和第 6 部分。每一部分我们都这样处理：

1. 先确保加数 numi 不越界。如果一个数的某个数位上的数大于 0 且下标(低位从 0 开始)大于 9 则一定越界，如第 46 行。如果数位下标等于 9 且数位上的数字大于 2 则也越界，如第 48 行。
2. 加数 numi 不越界，但和 sum 的和仍可能越界，所以加数 numi 不能超过 INT_MAX - sum。

6. LeetCode 11.盛最多水的容器

---

  题目。

$$图6盛最多水的容器$$

  分析：使用两层循环穷举任意两条线组成的容器，保留最大容积。这样的方法时间复杂度是 $O(n^2)$。
  双指针法：容器的容积由宽和高共同决定。在本题中，高是无序的，宽是有序的。所以我们可以按宽由大到小的顺序考察：第 1 条线和最后 1 条线组成的容器宽度最大，宽度确定后，容器的容积就由最短的边决定。因为第 1 条线比最后 1 条线短，所以可以得出结论：以第 1 条线为边界的容器，其最大容积是它的长度乘以它与最后 1 条线的距离。这样我们就把第 1 条线的情况考虑完了。
  根据上面的讨论可以总结规律：使用两个指针分别指向第 1 条线和第 n 条线，其容积为较短的那条线的长度乘以宽度，然后指向较短的那条线的指针移动一次，把较短的线排除。以此类推直到两个指针相邻。

class Solution {
public:
	int maxArea(vector<int>& height) {
		if (height.size() < 2)
			return 0;

		int res = 0, left = 0, right = height.size() - 1, width = height.size() - 1;
		while (left < right) {
			res = max(res, min(height[left], height[right]) * width);
			if (height[left] < height[right])
				left++;
			else
				right--;
			width--;
		}
		return res;
	}
};

  性能：时间复杂度是 $O(n)$，空间复杂度是 $O(1)$。

7. LeetCode 12.整数转罗马数字

---

  题目。

$$表7整数转罗马数字$$

  分析：由表 7 可以看出，整数转罗马数字时，可以把整数的每个数位上的数 x 分为 5 种情况处理：1<=x<=3、x=4、x=5、6<=x<=8、x=9。当 1<=x<=3 时，x 转换为 x 个 ‘I’、‘X’、‘C’ 或 ‘M’；当 x=4 时，x 转换为 “IV”、“XL”、或 “CD”；当 x=5 时，x 转换为 “V”、“L”、或 “D”；…
  个位上的 ‘I’,‘V’,‘X’ 相对于十位上的 ‘X’,‘L’,‘C’，相对于百位上的 ‘C’,‘D’,‘M’，相对于千位上的 ‘M’,’-’,’-’。其中 ‘-’ 用不到。所以我们把这四组存在二维数组中。

class Solution {
public:
	string intToRoman(int num) {
		if (num < 1)
			return "";

		char rome[][3] = { { 'I','V','X' },{ 'X','L','C' },{ 'C','D','M' },{'M','-','-'} };
		vector<string> res;
		string str;
		int x, index = 0;
		while (num != 0) {
			int x = num % 10;
			str.clear();
			if (x <= 3) {
				for (int i = 1; i <= x; i++) {
					str.push_back(rome[index][0]);
				}
			}
			else if (x == 4) {
				str.push_back(rome[index][0]);
				str.push_back(rome[index][1]);
			}
			else if (x == 5) {
				str.push_back(rome[index][1]);
			}
			else if (x >= 6 && x <= 8) {
				str.push_back(rome[index][1]);
				for (int i = 6; i <= x; i++)
					str.push_back(rome[index][0]);
			}
			else {
				str.push_back(rome[index][0]);
				str.push_back(rome[index][2]);
			}
			res.push_back(str);
			num /= 10;
			index++;
		}
		string res_str;
		for (int i = res.size() - 1; i >= 0; i--)
			res_str += res[i];
		return res_str;
	}
};

8. LeetCode 15.三数之和

---

  题目。
  注意：以某个数 x 开头的三元组可能有多个。
  分析：如果不排序，可以使用时间复杂度为 $O(n^3)$ 的算法。如果排序，因为使用双指针法可以设计时间复杂度为 $O(n)$ 的算法在有序数组中找出和为某个数的所有二元组，所以本题使用双指针法可以实现时间复杂度为 $O(n^2)$ 的算法。

class Solution {
public:
	vector<vector<int>> threeSum(vector<int>& nums) {
		if (nums.size() < 3)
			return{};
		// 1.排序。
		sort(nums.begin(), nums.end());
		vector<vector<int>> res, temp;
		// 2.避免重复：先执行一次获取last。
		temp = twoSum(nums, 0);
		for (auto x : temp)
			res.push_back(x);
		int last = nums[0];
		// 3.主要部分。
		for (int i = 1; i < nums.size(); i++) {
			if (nums[i] > 0)
				break;
			if (nums[i] == last)
				continue;
			temp.clear();
			// 4.固定一个数，查找二元组。
			temp = twoSum(nums, i);
			for (auto x : temp)
				res.push_back(x);
			last = nums[i];
		}
		// 5.如果三元组个数大于2，要去重复。
		if (res.size() < 2)
			return res;
		vector<vector<int>> no_repeat_res = { res[0] };
		int i = 0;
		for (auto vec : res)
			if (vec[0] != no_repeat_res[i][0] || vec[1] != no_repeat_res[i][1] || vec[2] != no_repeat_res[i][2]) {
				no_repeat_res.push_back(vec);
				i++;
			}
		return no_repeat_res;
	}
private:
	vector<vector<int>> twoSum(vector<int>& nums, int index) {
		vector<vector<int>> res;
		int left = index + 1, right = nums.size() - 1;
		int target = 0 - nums[index];
		while (left < right) {
			if (nums[left] + nums[right]>target)
				right--;
			else if (nums[left] + nums[right] < target)
				left++;
			else {
				res.push_back({ nums[index],nums[left],nums[right] });
				left++;
			}
		}
		return res;
	}
};

  注意：第 2 步和第 5 步都是为了去重复，这两个都不能少。如果没有第 5 步，输入 [0,0,0,0] 会 输出 [[0,0,0],[0,0,0]]。twoSum 函数中 left 从 index + 1 开始，而不是从 0 开始。

9. LeetCode 16.最接近的三数之和

---

  题目。
  分析：这一题和 LeeCode15 算法相同，所以时间复杂度也是 $O(n^2)$，但这一题的结果只是一个数，不用考虑结果是否有重复，所以更简单一些。

class Solution {
public:
	int threeSumClosest(vector<int>& nums, int target) {
		if (nums.size() < 3)
			return{};
		// 1.排序。
		sort(nums.begin(), nums.end());
		int res, min = INT_MAX;
		// 2.固定一个数，查找二元组。
		for (int i = 0; i < nums.size(); i++)
			twoSum(nums, target, i, min, res);
		return res;
	}
private:
	void twoSum(vector<int>& nums, int target, int index, int& min, int& res) {
		int left = index + 1, right = nums.size() - 1;
		while (left < right) {
			int three_num_sum = nums[index] + nums[left] + nums[right];
			if (abs(three_num_sum - target) < min) {
				res = three_num_sum;
				min = abs(three_num_sum - target);
			}
			if (three_num_sum > target)
				right--;
			else
				left++;
		}
	}
};

10. LeetCode 17.电话号码的字母组合

---

  题目。
  分析：该问题是求 n 个在指定范围内取值的字符的组合。类似于投掷 n 个骰子，求向上一面点数的集合。这既不是排列问题也不是组合问题，而是一个 n 重循环加回溯问题。

class Solution {
public:
	vector<string> letterCombinations(string digits) {
		if (digits.size() == 0)
			return {};
		// 1.完整的键盘。
		vector<vector<char>> keyboard = {
			{'a', 'b', 'c'}, {'d', 'e', 'f'},
			{'g', 'h', 'i'}, {'j', 'k', 'l'}, {'m', 'n', 'o'},
			{'p', 'q', 'r', 's'}, {'t', 'u', 'v'}, {'w', 'x', 'y', 'z'} };
		// 2.用到的按键。
		vector<vector<char>> keys;
		for (char ch : digits)
			keys.push_back(keyboard[ch - '2']);
		// 3.求按键上字母的组合。
		vector<string> res;
		permutation(keys, res);
		return res;
	}
private:
	void permutation(vector<vector<char>>& keys, vector<string>& res, int index = 0, string yi = string{}) {
		if (index == keys.size()) {
			res.push_back(yi);
			return;
		}
		for (int i = 0; i < keys[index].size(); i++) {
			yi.push_back(keys[index][i]);
			permutation(keys, res, index + 1, yi);
			yi.pop_back();
		}
	}
};

11. LeetCode 18.四数之和

---

  分析：这个题和《LeetCode 1.两数之和》、《LeetCode 15.三数之和》、《LeetCode 16.最接近的三数之和》方法相同。使用双指针法，求 m 数之和的时间复杂度为 $O(n^{m-1})$。

class Solution {
public:
	vector<vector<int>> fourSum(vector<int>& nums, int target) {
		if (nums.size() < 4)
			return {};
		sort(nums.begin(), nums.end());
		set<vector<int>> res;
		for (int idx1 = 0; idx1 < nums.size() - 3; idx1++)
			for (int idx2 = idx1 + 1; idx2 < nums.size() - 2; idx2++) {
				int idx3 = idx2 + 1, idx4 = nums.size() - 1;
				while (idx3 < idx4) {
					int sum = nums[idx1] + nums[idx2] + nums[idx3] + nums[idx4];
					if (sum == target) {
						res.insert({ nums[idx1], nums[idx2], nums[idx3], nums[idx4] });
						idx3++;
						idx4--;
					}
					else if (sum < target)
						idx3++;
					else
						idx4--;
				}
			}
		return vector<vector<int>>(res.begin(), res.end());
	}
};

  力扣的测试数据范围是 $-10^9$ 到 $10^9$，所以第 12 行使用 int 会越界，可以使用 long long 类型，也可以这样：

int sum12 = nums[idx1] + nums[idx2];
int sum34 = nums[idx3] + nums[idx4];
if (sum12 == target - sum34)

  重复的结果。为了避免结果中包含重复的四元数，先把结果存放在 set 中，再转移到 vector。

12. LeetCode 19.删除链表的倒数第 N 个结点（未实现）

---

  使用先后指针只需遍历一次。

13. LeetCode 22.括号生成

---

  这一题可以用回溯法解决。

class Solution {
public:
	vector<string> generateParenthesis(int n) {
		if (n < 1)
			return {};
		vector<string> res;
		backtrack(n, n, res);
		return res;
	}
private:
	void backtrack(int left, int right, vector<string>& res, string yi = string{}) {
		if (left == 0 && right == 0) {
			res.push_back(yi);
			return;
		}
		// 1.只要左括号还有剩余，就可以放左括号。
		if (left > 0) {
			yi.push_back('(');
			backtrack(left - 1, right, res, yi);
			yi.pop_back();
		}
		// 2.只有剩余的右括号多于剩余的左括号时，才可以放右括号。
		if (right > left) {
			yi.push_back(')');
			backtrack(left, right - 1, res, yi);
			yi.pop_back();
		}
	}
};

  回溯法的时间复杂度复杂，这里不讨论。我们的算法使用 yi 存放结果的一种可能，所以空间复杂度是 $O(n)$。

14. LeetCode 24.两两交换链表中的结点（未实现）

---

15. LeetCode 29.两数相除

---

  这个题与求快速幂的 LeetCode50:《Pow(x, n)》求解思想相同。
  商的意义是被除数中包含几个除数。不用除法求商，可以用被除数减除数，直到被除数小于除数，被除数减除数的次数就是商的整数部分。这种方法可行，但效率低，我们可以仿造快速幂的思想提高效率。先来看个例子，求 100 除以 3 的整数部分：

1. 100 大于 3 说明 100 中至少有 1 个 3，100 大于 6 说明 100 中至少有 2 个 3，100 大于 12 说明 100 中至少有 4 个 3，…，100 大于 96 说明 100 中至少有 32 个 3，100 小于 192 说明 100 中没有 192 个 3。至此我们只用 6 步就发现 100 中包含 32 个 3，这比每次减 3 需要 32 步快多了。然后 100 减去 32 个 3 得 4，因为 4 比 3 大，我们还要继续判断 4 中包含多少个 3。
2. 4 大于 3 说明 4 中至少有 1 个 3，4 小于 6 说明 4 中没有 2 个 3。至此我们发现 4 中包含 1 个 3。然后 4 减 3 得 1，因为 1 比 3 小，所以剩下的数中不包含 3 了，结束寻找过程。

  在第 1 步找到 32 个 3，在第 2 步找到 1 个 3，所以 100 中共有 33 个 3。上面的寻找过程主要是逐步判断被除数是否大于除数、除数的 2 倍，除数的 4 倍，除数的 8 倍…

class Solution {
public:
	int divide(int dividend, int divisor) {
		if (divisor == 0)
			throw exception("Divisor can not be zero!");
		// 1.确定符号。
		bool positive = (dividend ^ divisor) >= 0 ? true : false;
		// 2.转换成正数。
		long long lldividend = dividend, lldivisor = divisor, res = 0;
		lldividend = abs(lldividend), lldivisor = abs(lldivisor);
		// 3.核心算法。
		while (lldividend >= lldivisor) {
			// 4.求最大的 i，使 lldivisor * 2^i <= lldividend。
			long long lldivisor_pow2i = lldivisor;
			int left_move_time = 0;
			while ((lldivisor_pow2i << 1) <= lldividend) {
				lldivisor_pow2i <<= 1;
				left_move_time++;
			}
			res += pow(2, left_move_time);
			lldividend -= lldivisor_pow2i;
		}
		// 5.检查越界。
		res = positive == true ? res : 0 - res;
		if (res >= INT_MAX)
			return INT_MAX;
		else if (res <= INT_MIN)
			return INT_MIN;
		else
			return res;
	}
};

  越界问题。第 2 部分把负数转换成正数。$INT\_MIN=-2^{31},INT\_MAX=2^{31}-1$，当负数是 INT_MIN 时，32 位的 int 类型无法存放其相反数，只能使用 64 位长整型 long long 存放。一定要先转换成长整型再取绝对值，而不能先取绝对值再转换成长整型，因为对 INT_MIN 取绝对值会越界：abs(INT_MIN) = INT_MIN。

16. LeetCode 31.下一个排列

---

  这一题是求全排列的非递归算法的关键，详细的分析过程在全排列。

class Solution {
public:
	void nextPermutation(vector<int>& nums) {
		if (nums.size() < 2)
			return;
		// 1.从尾部开始找出第一个长度为2的递增子串。
		int p = nums.size() - 1;
		while (p > 0) {
			if (nums[p - 1] < nums[p])
				break;
			p--;
		}
		// 2.当前的排列是最大的，翻转它得到下一个最小排列。
		if (p == 0) {
			reverse(nums, 0);
			return;
		}
		// 3.从递减子串nums[p:n-1]的尾部开始查找第一个大于nums[p-1]的元素nums[min_index]。
		int min_index = nums.size() - 1;
		while (nums[min_index] <= nums[p - 1])
			min_index--;
		// 4.交换nums[p-1]与nums[min_index]。
		swap(nums[p - 1], nums[min_index]);
		// 5.把递减子串nums[p:n-1]翻转成递增子串。
		reverse(nums, p);
	}
private:
	void reverse(vector<int>& nums, int start) {
		int end = nums.size() - 1;
		while (start < end) {
			swap(nums[start], nums[end]);
			start++;
			end--;
		}
	}
};

  特别注意第 20 行是小于等于号，不要写成小于号。

17. LeetCode 33.搜索旋转排序数组

---

  这一题考察在旋转数组中查找 target。因为有序，所以可以使用二分查找。
  这一题的数组中的元素各不相同，也就是说旋转数组的前后两个递增子串都是严格递增的。LeetCode 81《搜索旋转排序数组 II》没有限制输入的元素各不相同，增加了难度。
  与旋转数组相关的题目还有 LeetCode 189《旋转数组》，考察怎么用 O(1) 的空间复杂度生成旋转数组；《剑指 Offer 第2版》第 11 题《旋转数组的最小数字》查找旋转数组的最小值。
  这里的 3.2 节详细讲解了在旋转数组中查找最小值、最大值和任意值的算法。

18. LeetCode 34.在排序数组中查找元素的第一个和最后一个位置（未实现）

---

19. LeetCode 36.有效的数独

---

  遍历三次、使用一个长度最长为 9 的 set：每次遍历时，使用 set 保存一行、一列或一个小区域内的字符以便检查重复。

class Solution {
public:
	bool isValidSudoku(vector<vector<char>>& board) {
		if (board.size() != 9 || board[0].size() != 9)
			return false;

		unordered_set<char> ust;
		// 1.检查每一行。
		for (int i = 0; i < 9; i++) {
			ust.clear();
			for (int j = 0; j < 9; j++) {
				if (board[i][j] == '.')
					continue;
				if (ust.count(board[i][j]) == 1)
					return false;
				ust.insert(board[i][j]);
			}
		}
		// 2.检查每一列。
		for (int j = 0; j < 9; j++) {
			ust.clear();
			for (int i = 0; i < 9; i++) {
				if (board[i][j] == '.')
					continue;
				if (ust.count(board[i][j]) == 1)
					return false;
				ust.insert(board[i][j]);
			}
		}
		// 3.检查每个小区域。
		for (int cx = 1; cx < 9; cx += 3) {
			for (int cy = 1; cy < 9; cy += 3) {
				ust.clear();
				for (int i = cx - 1; i <= cx + 1; i++) {
					for (int j = cy - 1; j <= cy + 1; j++) {
						if (board[i][j] == '.')
							continue;
						if (ust.count(board[i][j]) == 1)
							return false;
						ust.insert(board[i][j]);
					}
				}
			}
		}
		return true;
	}
};

  遍历一次、使用 27 个长度最长为 9 的 set：

class Solution {
public:
	bool isValidSudoku(vector<vector<char>>& board) {
		if (board.size() != 9 || board[0].size() != 9)
			return false;
			
		vector<unordered_multiset<char>> usts(27);
		for (int i = 0; i < 9; i++){
			for (int j = 0; j < 9; j++) {
				if (board[i][j] == '.')
					continue;
				if (usts[i].count(board[i][j]) > 0)
					return false;
				if (usts[9 + j].count(board[i][j]) > 0)
					return false;
				if (usts[18 + i / 3 * 3 + j / 3].count(board[i][j]) > 0)
					return false;
				usts[i].insert(board[i][j]);
				usts[9 + j].insert(board[i][j]);
				usts[18 + i / 3 * 3 + j / 3].insert(board[i][j]);
			}
		}
		return true;
	}
};

20. LeetCode 38.外观数列

---

class Solution {
public:
	string countAndSay(int n) {
		if (n <= 0)
			return "";
			
		string res = "1";
		vector<pair<int, char>> statistics;
		for (int i = 2; i <= n; i++) {
			// 1.统计外观数列的每个组。
			statistics.push_back({ 1,res[0] });
			char last_char = res[0];
			for (int j = 1; j < res.size(); j++) {
				if (res[j] == last_char)
					statistics.back().first++;
				else {
					statistics.push_back({ 1,res[j] });
					last_char = res[j];
				}
			}
			// 2.根据统计结果生成新的外观数列。
			res.clear();
			for(int i = 0; i < statistics.size(); i++) {
				res.push_back(statistics[i].first + '0');
				res.push_back(statistics[i].second);
			}
			statistics.clear();
		}
		return res;
	}
};

21. LeetCode 39.组合总和

---

  该题的数据量和数据范围都比较小，意味着除分治算法外，难以找到其它好方法。
  该题和《LeetCode 1.两数之和》、《LeetCode 15.三数之和》、《LeetCode 16.最接近的三数之和》、《LeetCode 18.四数之和》同是求和，区别在于该题求和的加数个数没有限制，这就类似《LeetCode 10.正则表达式匹配》，可以使用分治算法。

class Solution {
public:
	vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
		if (candidates.size() == 0)
			return{};

		set<vector<int>> pre_res;
		DAC(candidates, target, pre_res);
		backtrack(candidates, target, pre_res);
		vector<vector<int>> res(pre_res.begin(), pre_res.end());
		return res;
	}
private:
	void DAC(vector<int>& candidates, int target, set<vector<int>>& res, vector<int> yi = {}, int index = 0, int sum = 0) {
		if (sum > target || index >= candidates.size())
			return;
		if (sum == target) {
			res.insert(yi);
			return;
		}

		DAC(candidates, target, res, yi, index + 1, sum);
		yi.push_back(candidates[index]);
		sum += candidates[index];
		DAC(candidates, target, res, yi, index, sum);
		DAC(candidates, target, res, yi, index + 1, sum);
	}
	void backtrack(vector<int>& candidates, int target, set<vector<int>>& res, vector<int>& yi = vector<int>{}, int index = 0, int sum = 0) {
		if (sum > target || index >= candidates.size())
			return;
		if (sum == target) {
			res.insert(yi);
			return;
		}

		// 1.不使用candidates[index]。
		backtrack(candidates, target, res, yi, index + 1, sum);
		// 2.使用candidates[index]。
		yi.push_back(candidates[index]);
		sum += candidates[index];
		// 2.1继续使用candidates[index]。
		backtrack(candidates, target, res, yi, index, sum);
		// 2.2不再使用candidates[index]。
		backtrack(candidates, target, res, yi, index + 1, sum);
		// 撤销2。
		// sum -= yi.back();
		yi.pop_back();
	}
};

  该题还给出了回溯算法版的分治算法。它们的区别在于形参 yi，分治算法中的 yi 是值传递，递归函数栈中的每个函数都会有一个 yi 副本；回溯算法中的 yi 是引用传递，所有递归函数共享一个 yi 的实参，这样节省的内存是很明显的：

  本题中函数的形参尽量都使用默认参数。函数 backtrack 的第 4 个引用类型的形参 yi 也被赋予默认参数，有些编译器是不支持这样的，比如力扣。这时需要传递过来一个实参。
  题目中说了 candidates 中的元素是正整数，如果没有限定正数，不应该在 “sum > target” 时 return。为了避免结果中出现重复，本题先把结果保存在 set 中，再把 set 中的结果放入 vector。

22. LeetCode 40.组合总和Ⅱ（未实现）

---

23. LeetCode 43.字符串相乘

---

  分析与解决在 数学算法。

24. LeetCode 45.跳跃游戏Ⅱ

---

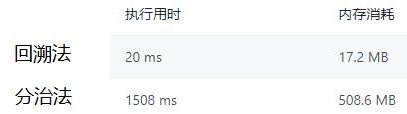
  我首先想到的是下面的分治算法。题目限定 1 <= nums.length <= 10000，所以下面的分治算法果然在长度为 39 的第 73/106 个测试数据 x73 上超时了。经测试，使用 x73 的后 35 个元素可以在几秒内计算出答案，但使用完整的 x73 等待很久还是不能得出答案。

class Solution {
public:
	int jump(vector<int>& nums) {
		if (nums.size() <= 1)
			return 0;

		int res = INT_MAX;
		DAC(nums, res);
		return res;
	}
private:
	void DAC(vector<int>& nums, int& step, int yi = 0, int location = 0) {
		if (location >= nums.size())
			return;
		if (location == nums.size() - 1)
			step = min(step, yi);

		for (int i = 1; i <= nums[location]; i++)
			DAC(nums, step, yi + 1, location + i);
	}
};
// vector x73 = { 5,6,4,4,6,9,4,4,7,4,4,8,2,6,8,1,5,9,6,5,2,7,9,7,9,6,9,4,1,6,8,8,4,4,2,0,3,8,5 };

  上面的分治算法是一种穷举算法，它枚举了所有可能的跳跃。下面我们找高效的枚举方法。
  分析数组 nums = { 2,5,3,1,1,1,9,1,1,1}。我们很容易知道最少需要 3 步就能到达末尾，其中第 3 步要从 9 开始跳。现在我们从头分析，第 1 步可以调到 5 和 3，我们应该跳到哪一个呢？如果跳到 5，下一步可以跳的范围是 (nums[2], nums[6])；如果跳到 3，下一步可以跳的范围是 (nums[3], nums[5])。因为通过前者可以跳得更远，下次选择的范围更大，所以应该跳到 5。

class Solution {
public:
	int jump(vector<int>& nums) {
		if (nums.size() <= 1)
			return 0;
			
		return DAC1(nums);
	}
private:
	int DAC1(vector<int>& nums, int location = 0) {
		if (location == nums.size() - 1)
			return 0;
		if (location + nums[location] >= nums.size() - 1)
			return 1;
			
		int min_stop = location + 1, max_stop = location + nums[location];
		int stop = find_stop(nums, min_stop, max_stop);
		return 1 + DAC1(nums, stop);
	}
	int DAC2(vector<int>& nums, int location = 0, int last_max_stop = 0) {
		if (location == nums.size() - 1)
			return 0;
		if (location + nums[location] >= nums.size() - 1)
			return 1;
			
		int min_stop = last_max_stop + 1, max_stop = location + nums[location];
		int stop = find_stop(nums, min_stop, max_stop);
		return 1 + DAC2(nums, stop, max_stop);
	}
	int find_stop(vector<int>& nums, int start, int end) {
		int stop = start, next_span = start + nums[start];
		for (int i =start + 1; i <= end; i++) {
			if (i + nums[i] > next_span) {
				stop = i;
				next_span = i + nums[i];
			}
		}
		return stop;
	}
};

25. LeetCode 64.最小路径

---

  本题求的是从左上角到右下角的最小路径，可以直接返回 dp[H - 1][W - 1]。如果求的是从左上角到底部的最小路径，应该返回 dp[H - 1] 的最小值。

class Solution {
public:
	int minPathSum(vector<vector<int>>& grid) {
		if (grid.size() == 0)
			return 0;

		int H = grid.size(), W = grid[0].size();
		vector<vector<int>> dp(H, vector<int>(W));
		for (int y = 0; y < H; y++) {
			for (int x = 0; x < W; x++) {
				if (y == 0 && x == 0)
					dp[y][x] = grid[y][x];
				else if (y == 0)
					dp[y][x] = dp[y][x - 1] + grid[y][x];
				else if (x == 0)
					dp[y][x] = dp[y - 1][x] + grid[y][x];
				else
					dp[y][x] = min(dp[y][x - 1], dp[y - 1][x]) + grid[y][x];
			}
		}
		return dp[H - 1][W - 1];
	}
};