牛客小白月赛68

小白月赛68

写在前面：今年开春被一些乱七八糟的事情耽误了很久，断断续续帮别人解决了一些问题，但直到今天才打了今年第一场比较正式的比赛，2023年的第一场AK局，在人生择业的三岔路口，我当前唯一能确信的是我仍然爱着coding，以后的事以后再说吧。鸽了很久的实习、论文、秋招历程等以后有时间之后再更新吧（不会再拖了，最迟六月份结束之前吧，也差不多该给自己的竞赛和学术生涯写一封遗书了）。回归正题，A-E应该都能秒过，F感觉差不多是常数级别的优化，中途wa了两发，可能是近期写的最恶心的题目之一了。

比赛网址

A. Tokitsukaze and New Operation

思路： 签到题，不做解释。

代码：

#include 
using namespace std;
const int N = 15;
char s1[N], s2[N];

int main(){
    int T;
    cin >> T;
    while(T--){
        cin >> s1 >> s2;
        int len = strlen(s1);
        if(len != strlen(s2)){
            cout << "-1\n";
            continue;
        }
        for(int i = 0; i < len; i++)
            cout << (s1[i]-'0')*(s2[i]-'0');
        cout << "\n";
    }
    return 0;
}

B. Tokitsukaze and Order Food Delivery

思路： 暴力的解法套了个背包的题面，暴力扫一遍所有店铺中的所有商品，取最小值即可，注意不要取负值。

代码：

#include 
using namespace std;
const int N = 1e5+5;
const int MAXN = 1e9+50;
int n, a, b;

int main(){
    int T;
    cin >> T;
    while(T--){
        int ans = MAXN;
        cin >> n >> a >> b;
        int k, x, y;
        for(int i = 0; i < n; i++){
            cin >> k >> x >> y;
            int v;
            for(int j = 0; j < k; j++){
                cin >> v;
                int tmp = v;
                if(v >= x) tmp -= y;
                if(v >= a) tmp -= b;
                tmp = max(tmp, 0);
                ans = min(tmp, ans);
            }
        }
        cout << ans << "\n";
    }
    return 0;
}

C. Tokitsukaze and Average of Substring

思路： n的上限为5000，n^2的解法可行，考虑枚举左右端点L和R，然而每次在计算完[l,r]范围内的C，即C(l, r)再计算C(l, r+1)时若再重复计算[l, r]会增加一个n的代价，无疑会超时，这里我们可以看到对于s[r+1]，他对于C(l, r)的贡献为s[r+1]在[l, r]区间内出现的次数，因此我们在确定左端点l后，只需要记录每个字符在[l,r]范围内出现的次数并更新即可。简单来说，我们将s[r+1]在[l, r]内出现的次数定义为cnt(s[r+1])，则我们可以轻易得出C(l, r+1) = C(l, r)+cnt(s[r+1])，这样优化掉一层n后可以直接n ^2暴力枚举即可。

代码：

#include 
#define ll long long 
#define mem(f, x) memset(f, x, sizeof(f))
using namespace std;
const int M = 30;
const int N = 5005;
char s[N];
int n;
int cnt[M];

int main(){
    int T;
    cin >> T;
    while(T--){
        cin >> n;
        cin >> s+1;
        for(int i = 0; i < M; i++)
            cnt[i] = 0;
        
        double ans = 0;
        for(int i = 1; i <= n; i++){
            for(int j = 0; j < M; j++)
                cnt[j] = 0;
            int pre = 0;
            for(int j = i; j <= n; j++){
                int id = s[j] - 'a';
                pre += cnt[id];
                cnt[id]++;
                ans = max(ans, pre*1.0/(j-i+1));
            }
        }
        printf("%.6lf\n", ans);
    }
    return 0;
}

D. Tokitsukaze and Development Task

思路： 粗看是个多重背包的dp，但是出题人简化了一下，三层的资源相互独立，对应的操作也是相互独立，只需BFS计算每一层所需操作的最少次数然后相加即可，唯一需要注意的是上下界合规性的判定以及已经经历过的状态用vis记录后可以有效剪枝。

代码：

#include 
#define mem(f, x) memset(f, x, sizeof(f))
using namespace std;
const int N = 305;
int a, b, c, d;
bool vis[N];

bool judge(int x){
    if(x < 10 || x > 300 || vis[x])
        return 0;
    return 1;
}

int BFS(int target){
    queue<int> q;
    q.push(10);
    set<int> st;
    mem(vis, 0);
    vis[10] = 1;
    int cnt = 0;
    while(!q.empty()){
        int num = q.size();
        for(int i = 0; i < num; i++){
            int cur = q.front();
            q.pop();
            if(cur == target)
                return cnt;
            int next = cur-1;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = cur+1;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = cur+10;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = cur-10;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = cur+100;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = cur-100;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = 300;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
            next = 10;
            if(judge(next)){
                vis[next] = 1;
                q.push(next);
            }
        }
        cnt++;
    }
    return 0;
}

int main(){
    int T;
    cin >> T;
    while(T--){
        cin >> a >> b >> c >> d;
        printf("%d\n", BFS(a)+BFS(b)+BFS(c)+BFS(d));
    }
    return 0;
}

E. Tokitsukaze and Colorful Chessboard

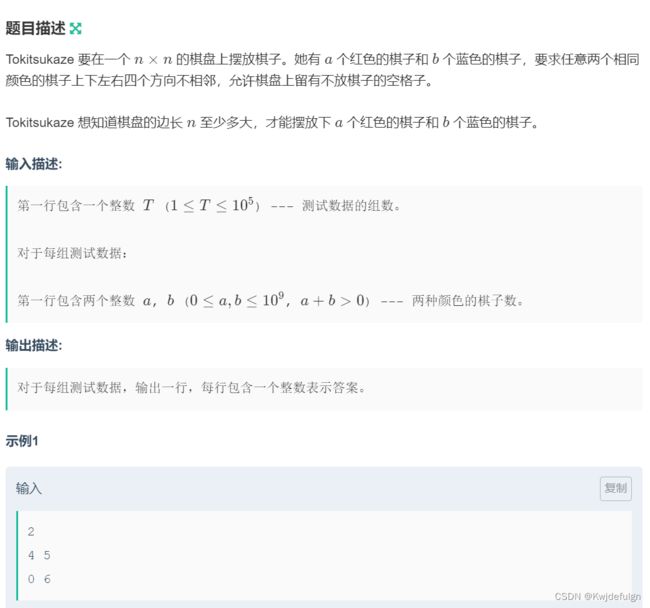
思路： 两类旗子考虑数量较多的那一类，由于不能上下左右相邻放置，我们记F(n)为边长为n的正方形最多可以放置的满足条件的棋子数，则F(n) = (n^2+1)/2，即面积的一半，若边长为奇，则应该比一半多一个（自己画个图填一下就能找到规律了）。现已知棋子数，求满足正方形的最小边长，由于边长单调递增，这里直接二分边长即可，唯一需要注意的就是边界的处理，举个例子，红棋和蓝棋都为1个，若取最大值后，二分的结果n=1，即边长为1的正方形就能放下一个棋子，胆子红蓝各有一个，因此n=1放不下，因此这里当红棋数=蓝棋数且数量都为奇数时需要将二分的目标值加一。

代码：

#include 
#define ll long long
#define mem(f, x) memset(f, x, sizeof(f))
using namespace std;
const int N = 305;


int main(){
    int T;
    cin >> T;
    while(T--){
        ll a, b;
        cin >> a >> b;
        if(a == b && a&1) a++;
        else a = max(a, b);
        ll L = 1, R = 1e5+5;
        while(L <= R){
            ll mid = (L+R) / 2;
            ll tmp = (mid*mid+1)/2;
            if(tmp < a) L = mid+1;
            else R = mid-1;
        }
        cout << L << "\n";
    }
    return 0;
}

F. Tokitsukaze and New RenKinKama

思路： 我们将不符合条件的点看做是坏点，由于最多只能进行两次交换操作，易知每次如果交换的是两个好点，那么本次操作是没有意义的。所以每次的操作只有两种可能：

1. 坏点和坏点交换
2. 坏点和好点交换

另外，由于最多只能进行两次交换，因此当总的坏点数超过12时，那么两次以内的交换操作一定不可能使所有的点变成好点。考虑最极端的情况：
1，1e9，1，…1，1e9，1，每次的交换操作最多只能使6个坏点变好，因此两次交换操作能使坏点变好的上限为12。

用上述几点剪枝后，直接暴力枚举坏点交换完后直接check是否合规即可（建议自己写一遍，细节不太好写，我自己比赛的时候写了40多分钟才把思路理顺）。

代码：

#include 
#define ll long long
#define pii pair<int,int>
#define pb push_back
#define fi first 
#define se second
#define mem(f, x) memset(f, x, sizeof(f))
using namespace std;
const int N = 305;
int v[N], n, k, flag;
vector<pii> ans;

bool judge(){
    for(int i = 0; i < n; i++)
        if(abs(v[(i+1)%n]-v[i]) > k) return 0;
    return 1;
}

void op(int id){
    for(int i = 0; i < n; i++){
        if(i == id) continue;
        ans.pb({id, i});
        swap(v[id], v[i]);
        if(judge()){
            flag = 1;
            return;
        }
        ans.pop_back();
        swap(v[id], v[i]);
    }
}

void change(int id){
    for(int i = 0; i < n; i++){
        if(i == id) continue;
        swap(v[id], v[i]);
        ans.pb({id, i});
        if(judge()){
            flag = 1;
            return;
        }
        for(int i = 0; i < n; i++){
            int next = (i+1)%n;
            if(abs(v[next]-v[i]) > k){
                op(i);
                if(!flag) op(next);
                if(flag) return;
                break;
            }
        }
        ans.pop_back();
        swap(v[id], v[i]);
    }
}

int main(){
    int T;
    cin >> T;
    while(T--){
        cin >> n >> k;
        for(int i = 0; i < n; i++)
            cin >> v[i];
        if(n == 1 || judge()){
            cout << "0\n";
            continue;
        }
        int cnt = 0;
        for(int i = 0; i < n; i++){
            if(abs(v[(i+1)%n]-v[i]) > k)
                cnt++;
        }
        if(cnt > 12){
            cout << "-1\n";
            continue;
        }
        flag = 0;
        ans.clear();
        for(int i = 0; i < n; i++){
            int next = (i+1)%n;
            if(abs(v[next]-v[i]) > k){
                change(i);
                if(!flag) change(next);
                break;
            }
        }
        if(flag){
            cout << ans.size() << "\n";
            for(auto &item:ans)
                cout << item.fi+1 << " " << item.se+1 << "\n";
        }else
            cout << "-1\n";
    }
    return 0;
}