数据结构——二叉树的应用

实验预备知识：

1. 熟练掌握二叉树的概念及5大性质。
2. 掌握二叉树的非递归遍历及递归遍历的方法。
3. 能利用二叉树的遍历解决实际问题。
4. 理解树和二叉树的含义、目的和处理方法。

一、实验目的

1. 理解和掌握树及二叉树的类型定义方法。
2. 定义二叉树的基本存储结构，实现基本运算
3. 学习利用树及二叉树解决实际问题

二、实验要求

【项目1】使用队列完成层次遍历，请将代码及验证结果填入以下表格中
程序代码：
main.cpp:

#include 
#include "btree.h"

using namespace std;

int main()
{
    char str[]="A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))";
    BTNode *b;
    int n=0;
    CreateBTNode(b,str);
    DispBTNode(b);
    printf("\n");
    Traversal(b);
    DestroyBTNode(b);
    return 0;
}

btree.cpp:

#include 
#include 
#include "btree.h"

void CreateBTNode(BTNode *&b,char *str)     //由str串创建二叉链
{
    BTNode *St[MaxSize],*p=NULL;
    int top=-1,k,j=0;
    char ch;
    b=NULL;             //建立的二叉树初始时为空
    ch=str[j];
    while (ch!='\0')    //str未扫描完时循环
    {
        switch(ch)
        {
        case '(':
            top++;
            St[top]=p;
            k=1;
            break;      //为左节点
        case ')':
            top--;
            break;
        case ',':
            k=2;
            break;                          //为右节点
        default:
            p=(BTNode *)malloc(sizeof(BTNode));
            p->data=ch;
            p->lchild=p->rchild=NULL;
            if (b==NULL)                    //p指向二叉树的根节点
                b=p;
            else                            //已建立二叉树根节点
            {
                switch(k)
                {
                case 1:
                    St[top]->lchild=p;
                    break;
                case 2:
                    St[top]->rchild=p;
                    break;
                }
            }
        }
        j++;
        ch=str[j];
    }
}
BTNode *FindNode(BTNode *b,ElemType x)  //返回data域为x的节点指针
{
    BTNode *p;
    if (b==NULL)
        return NULL;
    else if (b->data==x)
        return b;
    else
    {
        p=FindNode(b->lchild,x);
        if (p!=NULL)
            return p;
        else
            return FindNode(b->rchild,x);
    }
}
BTNode *LchildNode(BTNode *p)   //返回*p节点的左孩子节点指针
{
    return p->lchild;
}
BTNode *RchildNode(BTNode *p)   //返回*p节点的右孩子节点指针
{
    return p->rchild;
}
int BTNodeDepth(BTNode *b)  //求二叉树b的深度
{
    int lchilddep,rchilddep;
    if (b==NULL)
        return(0);                          //空树的高度为0
    else
    {
        lchilddep=BTNodeDepth(b->lchild);   //求左子树的高度为lchilddep
        rchilddep=BTNodeDepth(b->rchild);   //求右子树的高度为rchilddep
        return (lchilddep>rchilddep)? (lchilddep+1):(rchilddep+1);
    }
}
void DispBTNode(BTNode *b)  //以括号表示法输出二叉树
{
    if (b!=NULL)
    {
        printf("%c",b->data);
        if (b->lchild!=NULL || b->rchild!=NULL)
        {
            printf("(");
            DispBTNode(b->lchild);
            if (b->rchild!=NULL) printf(",");
            DispBTNode(b->rchild);
            printf(")");
        }
    }
}
void DestroyBTNode(BTNode *&b)   //销毁二叉树
{
    if (b!=NULL)
    {
        DestroyBTNode(b->lchild);
        DestroyBTNode(b->rchild);
        free(b);
    }
}
void preOrder(BTNode *b)
{
    if(b != NULL)
    {
        printf("%c",b->data);
        preOrder(b->lchild);
        preOrder(b->rchild);
    }
}
void countNode(BTNode *b,int &n)
{
    if(b!=NULL)
    {
        n++;
        countNode(b->lchild,n);
        countNode(b->rchild,n);
    }
}
void Traversal(BTNode *b)
{
    BTNode *temp;
    //定义顺序队列
    BTNode* que[MaxSize];
    int front = -1,rear = -1;
    //把根节点入队
    if(b == NULL)
        return;
    que[++rear]=b;
    while(front != rear)
    {
        //出队并显示队首元素
        front++;
        temp = que[front];
        printf("%c",temp->data);
        //把孩子节点做入队操作
        if(temp->lchild!=NULL)
        {
            que[++rear] = temp->lchild;
        }
        if(temp->rchild!=NULL)
        {
            que[++rear] = temp->rchild;
        }
    }
}

btree.h:

#ifndef BTREE_H_INCLUDED
#define BTREE_H_INCLUDED

#include 
#include 
#define MaxSize 100
typedef char ElemType;
typedef struct node
{
    ElemType data;              //数据元素
    struct node *lchild;        //指向左孩子
    struct node *rchild;        //指向右孩子
} BTNode;
void CreateBTNode(BTNode *&b,char *str);        //由str串创建二叉链
BTNode *FindNode(BTNode *b,ElemType x);     //返回data域为x的节点指针
BTNode *LchildNode(BTNode *p);  //返回*p节点的左孩子节点指针
BTNode *RchildNode(BTNode *p);  //返回*p节点的右孩子节点指针
int BTNodeDepth(BTNode *b); //求二叉树b的深度
void DispBTNode(BTNode *b); //以括号表示法输出二叉树
void DestroyBTNode(BTNode *&b);  //销毁二叉树

void preOrder(BTNode *b);
void countNode(BTNode *b,int &n);

void Traversal(BTNode *b);
#endif // BTREE_H_INCLUDED

运行结果截图：

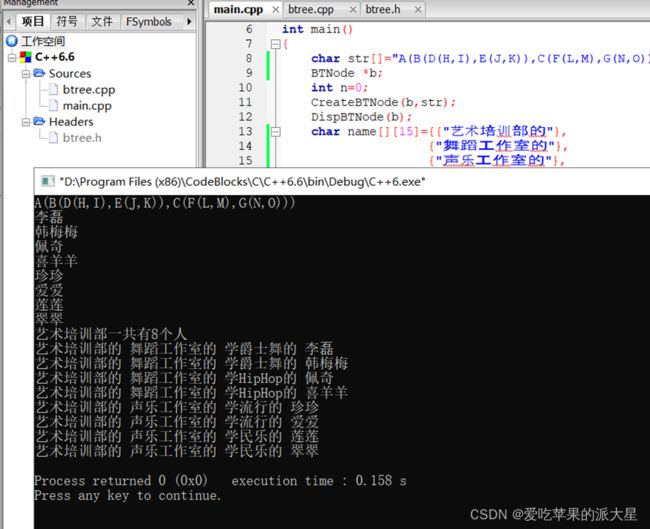
【项目2】----下图是某培训部的组织机构树状图，请在各机构的下面自行虚拟不超出2人的人员情况。完成以下操作：

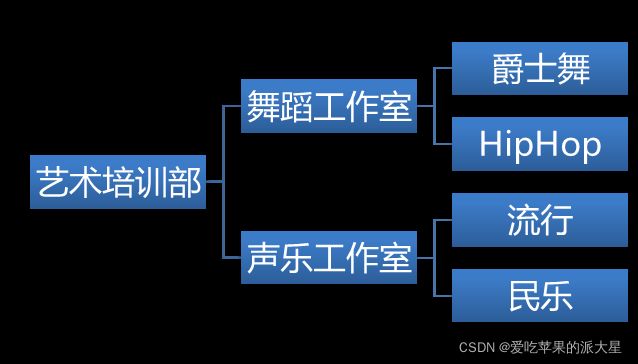
A（B(E,F(K,L)),C(G(M,N),H(O,P))）

【要求】：

1. 输出所有的人员，提示语为艺术培训部共有x人，分别为：xxx，xxx，xx
2. 输出每个人员的归属情况，比如艺术培训部门下舞蹈工作室下的爵士舞成员xxx
3. 利用上次实验的算法库来完成

程序代码：
Main.cpp:

#include 
#include "btree.h"

using namespace std;

int main()
{
    char str[]="A(B(D(H,I),E(J,K)),C(F(L,M),G(N,O)))";
    BTNode *b;
    int n=0;
    CreateBTNode(b,str);
    DispBTNode(b);
    char name[][15]={{"艺术培训部的"},
                    {"舞蹈工作室的"},
                    {"声乐工作室的"},
                    {"学爵士舞的"},{"学HipHop的"},
                    {"学流行的"},{"学民乐的"},
                    {"李磊"},{"韩梅梅"},{"佩奇"},{"喜羊羊"},
                    {"珍珍"},{"爱爱"},{"莲莲"},{"翠翠"}};
    printf("\n");
    countLeaf2(b,n,4,1,name);
    printf("艺术培训部一共有%d个人\n",n);
    path(b,name);
    DestroyBTNode(b);
    return 0;
}

Btree.cpp:

#include 
#include 
#include "btree.h"

void CreateBTNode(BTNode *&b,char *str)     //由str串创建二叉链
{
    BTNode *St[MaxSize],*p=NULL;
    int top=-1,k,j=0;
    char ch;
    b=NULL;             //建立的二叉树初始时为空
    ch=str[j];
    while (ch!='\0')    //str未扫描完时循环
    {
        switch(ch)
        {
        case '(':
            top++;
            St[top]=p;
            k=1;
            break;      //为左节点
        case ')':
            top--;
            break;
        case ',':
            k=2;
            break;                          //为右节点
        default:
            p=(BTNode *)malloc(sizeof(BTNode));
            p->data=ch;
            p->lchild=p->rchild=NULL;
            if (b==NULL)                    //p指向二叉树的根节点
                b=p;
            else                            //已建立二叉树根节点
            {
                switch(k)
                {
                case 1:
                    St[top]->lchild=p;
                    break;
                case 2:
                    St[top]->rchild=p;
                    break;
                }
            }
        }
        j++;
        ch=str[j];
    }
}
BTNode *FindNode(BTNode *b,ElemType x)  //返回data域为x的节点指针
{
    BTNode *p;
    if (b==NULL)
        return NULL;
    else if (b->data==x)
        return b;
    else
    {
        p=FindNode(b->lchild,x);
        if (p!=NULL)
            return p;
        else
            return FindNode(b->rchild,x);
    }
}
BTNode *LchildNode(BTNode *p)   //返回*p节点的左孩子节点指针
{
    return p->lchild;
}
BTNode *RchildNode(BTNode *p)   //返回*p节点的右孩子节点指针
{
    return p->rchild;
}
int BTNodeDepth(BTNode *b)  //求二叉树b的深度
{
    int lchilddep,rchilddep;
    if (b==NULL)
        return(0);                          //空树的高度为0
    else
    {
        lchilddep=BTNodeDepth(b->lchild);   //求左子树的高度为lchilddep
        rchilddep=BTNodeDepth(b->rchild);   //求右子树的高度为rchilddep
        return (lchilddep>rchilddep)? (lchilddep+1):(rchilddep+1);
    }
}
void DispBTNode(BTNode *b)  //以括号表示法输出二叉树
{
    if (b!=NULL)
    {
        printf("%c",b->data);
        if (b->lchild!=NULL || b->rchild!=NULL)
        {
            printf("(");
            DispBTNode(b->lchild);
            if (b->rchild!=NULL) printf(",");
            DispBTNode(b->rchild);
            printf(")");
        }
    }
}
void DestroyBTNode(BTNode *&b)   //销毁二叉树
{
    if (b!=NULL)
    {
        DestroyBTNode(b->lchild);
        DestroyBTNode(b->rchild);
        free(b);
    }
}
void preOrder(BTNode *b)
{
    if(b != NULL)
    {
        printf("%c",b->data);
        preOrder(b->lchild);
        preOrder(b->rchild);
    }
}
void countNode(BTNode *b,int &n)
{
    if(b!=NULL)
    {
        n++;
        countNode(b->lchild,n);
        countNode(b->rchild,n);
    }
}
void Traversal(BTNode *b)
{
    BTNode *temp;
    //定义顺序队列
    BTNode* que[MaxSize];
    int front = -1,rear = -1;
    //把根节点入队
    if(b == NULL)
        return;
    que[++rear]=b;
    while(front != rear)
    {
        //出队并显示队首元素
        front++;
        temp = que[front];
        printf("%c",temp->data);
        //把孩子节点做入队操作
        if(temp->lchild!=NULL)
        {
            que[++rear] = temp->lchild;
        }
        if(temp->rchild!=NULL)
        {
            que[++rear] = temp->rchild;
        }
    }
}
void countLeaf(BTNode *b,int &cnt)
{
    if(b!=NULL)
    {
        if(b->lchild == NULL && b->rchild == NULL)
            cnt++;
        else
        {
            countLeaf(b->lchild,cnt);
            countLeaf(b->rchild,cnt);
        }
    }
}
void countLeaf1(BTNode *b,int &cnt,int h,int i)
{
    if(b!=NULL)
    {
        if(b->lchild == NULL && b->rchild == NULL && i == h)
            cnt++;
        else
        {
            countLeaf1(b->lchild,cnt,h,i+1);
            countLeaf1(b->rchild,cnt,h,i+1);
        }
    }
}
void countLeaf2(BTNode *b,int &cnt,int h,int i,char name[][15])
{
    if(b!=NULL)
    {
        if(b->lchild == NULL && b->rchild == NULL && i == h)
        {
            cnt++;
            printf("%s\n",name[b->data-'A']);
        }
        else
        {
            countLeaf2(b->lchild,cnt,h,i+1,name);
            countLeaf2(b->rchild,cnt,h,i+1,name);
        }
    }
}
void path(BTNode *b,char name[][15])
{
    BTNode *temp;
    //定义顺序队列
    BTNode1 que[MaxSize];
    int front = -1,rear = -1;
    //把根节点入队
    if(b == NULL)
        return;
    que[++rear].node = b;
    que[rear].idx = -1;
    while(front != rear)
    {
        //出队并显示队首元素
        front++;
        temp = que[front].node;
        if(temp->lchild == NULL && temp->rchild == NULL)
        {
            int i = front;
            //定义顺序栈
            BTNode* stk[MaxSize];
            int top = -1;
            while(que[i].idx != -1)
            {
                stk[++top] = que[i].node;
                i = que[i].idx;
            }
            //做入栈操作
            stk[++top] = que[i].node;
            //输出路径
            while(top != -1)
            {
                printf("%s ",name[stk[top]->data-'A']);
                top--;
            }
            printf("\n");
        }
        //把孩子节点做入队操作
        if(temp->lchild!=NULL)
        {
            que[++rear].node = temp->lchild;
            que[rear].idx = front;
        }
        if(temp->rchild!=NULL)
        {
            que[++rear].node = temp->rchild;
            que[rear].idx = front;
        }
    }
}

Btree.h:

#ifndef BTREE_H_INCLUDED
#define BTREE_H_INCLUDED

#include 
#include 
#define MaxSize 100
typedef char ElemType;
typedef struct node
{
    ElemType data;              //数据元素
    struct node *lchild;        //指向左孩子
    struct node *rchild;        //指向右孩子
} BTNode;

typedef struct
{
    BTNode* node;
    int idx;
}BTNode1;

void CreateBTNode(BTNode *&b,char *str);        //由str串创建二叉链
BTNode *FindNode(BTNode *b,ElemType x);     //返回data域为x的节点指针
BTNode *LchildNode(BTNode *p);  //返回*p节点的左孩子节点指针
BTNode *RchildNode(BTNode *p);  //返回*p节点的右孩子节点指针
int BTNodeDepth(BTNode *b); //求二叉树b的深度
void DispBTNode(BTNode *b); //以括号表示法输出二叉树
void DestroyBTNode(BTNode *&b);  //销毁二叉树

void preOrder(BTNode *b);
void countNode(BTNode *b,int &n);

void Traversal(BTNode *b);
void countLeaf(BTNode *b,int &cnt);
void countLeaf1(BTNode *b,int &cnt,int h,int i);
void countLeaf2(BTNode *b,int &cnt,int h,int i,char name[][15]);

void path(BTNode *b,char name[][15]);
#endif // BTREE_H_INCLUDED

运行结果截图：