剑指offer读书笔记3(面试题39-52)
0503
剑指offer读书笔记3
- 面试题1-20
- 面试题21-38
- 第5章 优化时间和空间效率
-
- 5.2 时间效率
-
- 面试题39:数组中出现次数超过一半的数字
- 面试题40:最小的K个数
-
- 快速排序
- 堆排序
- queue deque priority_queued的比较
- 面试题41: 数据流中的中位数
- 面试题42:连续子数组的最大和(动态规划)
- 面试题43:1~n 整数中 1 出现的次数
- 面试题44:数字序列中某一位的数字
- 面试题45:把数组排成最小的数
- 面试题46:把数字翻译成字符串
- 面试题47:礼物的最大价值
- 5.3 时间效率与空间效率的平衡
-
- 面试题48:最长不含重复字符的子字符串
- 面试题49:丑数
-
- 补充:归并排序(分治 + 递归)
- 面试题50:字符串中第一个只出现一次的字符
-
- 相关题目:
- 补充:c++ unordered_map 3种遍历方式
- 面试题50':字符流中第一个只出现一次的字符
- 面试题51:数组中的逆序对
- 面试题52:两个链表的第一个公共结点
- 第6章 面试中的各项能力
面试题1-20
见剑指offer读书笔记1
面试题21-38
见剑指offer读书笔记2
第5章 优化时间和空间效率
5.2 时间效率
面试题39:数组中出现次数超过一半的数字
用前三种方法就行了,第四种看不懂,太绕了[捂脸]。
方法1:
比较笨的方法:用哈希表统计每个数字出现的次数。
(下面两种写法都可以,一个是找到出现的次数超过一半的元素;一个是找到出现次数最多的元素)
class Solution {
public:
int majorityElement(vector<int>& nums) {
//哈希表法:
unordered_map<int, int> hashTable;
//for(int i = 0; i < nums.size(); i++) ++hashTable[nums[i]];
for(int num : nums) ++hashTable[num];
//写法1:找到出现的次数超过一半的元素
int res;
for(auto it = hashTable.begin(); it != hashTable.end(); it++){
if(it->second > nums.size() / 2){
res = it->first;
break;
}
}
//写法2:找到出现次数最多的元素
int res, count = 0;
for(int x : nums) ++hashTable[x];
for(auto it = hashTable.begin(); it != hashTable.end(); it++){
if(it->second > count){
res = it->first;//数字
count = it->second;//数字出现的次数
}
}
//返回值:
return res;
}
};
方法2:
常规做法:给这个数组排序,然后位于**数组中间的数字(中位数)**一定就是那个出现次数超过数组长度一半的数字。
class Solution {
public:
int majorityElement(vector<int>& nums) {
//排序:
sort(nums.begin(), nums.end());
return nums[nums.size() / 2];
}
};
方法3:(很巧妙)
摩尔投票法:见剑指 Offer 39. 数组中出现次数超过一半的数字(摩尔投票法,清晰图解)
首先 int count = 0; int val;
然后遍历nums:
- 如果次数为0,就保存下一个数字,并把次数设为1;
- 如果次数不为0,
遇到下一个数字和之前保存的数字不相同,次数减1;
遇到下一个数字和之前保存的数字相同,次数加1;
最后返回val。
class Solution {
public:
int moreThanHalfNum_Solution(vector<int>& nums) {
//摩尔投票法:
int count = 0;
int val;
for(auto x : nums){
//如果次数为0,就保存下一个数字,并把次数设为1:
if(count == 0){
val = x;
count = 1;
}
else{//如果次数不为0
//遇到下一个数字和之前保存的数字不相同,次数减1
if(x != val)
count--;
//遇到下一个数字和之前保存的数字相同,次数加1
else
count++;
}
}
//最后一次把次数设为1时对应的数字就是要找的数字:
return val;
}
};
class Solution {
public:
int majorityElement(vector<int>& nums) {
//摩尔投票法:
int val, count = 0;
for(int num : nums){
if(count == 0){
val = num;
count = 1;
}
else{
if(num == val) ++count;
else --count;
}
}
return val;
}
};
方法4:(没怎么看懂[捂脸])
分治法(改变数组中数字的顺序的方法)
跟书上说的基于函数Partition()的方法还不一样,就用上面的三种方法。
下面的内容见数组中出现次数超过一半的数字
思路:
如果数 a 是数组 nums 的众数,如果我们将 nums 分成两部分,那么 a 必定是至少一部分的众数。
我们可以使用反证法来证明这个结论。假设 a 既不是左半部分的众数,也不是右半部分的众数,那么 a 出现的次数少于 l / 2 + r / 2 次,其中 l 和 r 分别是左半部分和右半部分的长度。由于 l / 2 + r / 2 <= (l + r) / 2,说明 a 也不是数组 nums 的众数,因此出现了矛盾。所以这个结论是正确的。
这样以来,我们就可以使用分治法解决这个问题:将数组分成左右两部分,分别求出左半部分的众数 a1 以及右半部分的众数 a2,随后在 a1 和 a2 中选出正确的众数。
算法:
我们使用经典的分治算法递归求解,直到所有的子问题都是长度为 1 的数组。长度为 1 的子数组中唯一的数显然是众数,直接返回即可。如果回溯后某区间的长度大于 1,我们必须将左右子区间的值合并。如果它们的众数相同,那么显然这一段区间的众数是它们相同的值。否则,我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。
代码:
class Solution {
int count_in_range(vector<int>& nums, int target, int lo, int hi) {
int count = 0;
for (int i = lo; i <= hi; ++i)
if (nums[i] == target)
++count;
return count;
}
int majority_element_rec(vector<int>& nums, int lo, int hi) {
if (lo == hi)
return nums[lo];
int mid = (lo + hi) / 2;
int left_majority = majority_element_rec(nums, lo, mid);
int right_majority = majority_element_rec(nums, mid + 1, hi);
if (count_in_range(nums, left_majority, lo, hi) > (hi - lo + 1) / 2)
return left_majority;
if (count_in_range(nums, right_majority, lo, hi) > (hi - lo + 1) / 2)
return right_majority;
return -1;
}
public:
int majorityElement(vector<int>& nums) {
return majority_element_rec(nums, 0, nums.size() - 1);
}
};
面试题40:最小的K个数
3种方法:
- 排序,然后输出前k的数;
- 堆排序:
我们用一个大根堆实时维护数组的前k小值。首先将前k个数插入大根堆中,随后从第k+1个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数(最大值)弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。
补充:
①大根堆:根的值最大;
②C++ 语言中的堆(即优先队列)为大根堆
③c++中的堆-priority_queue的使用方法:大根堆就是个优先队列priority_queue,用法和队列相似。 - 快速排序:
基于函数Partition()的方法(函数Partition()在剑指offer读书笔记1的2.4.2中有讲到)
如果基于数组的第k个数字来调整,则使得比第k个数字小的所有数字都位于数组的左边,比第k个数字大的所有数字都位于数组的右边,此时数组中左边的k个数字就是最小的k个数字
注意:这k个数字不一定是排序的,而且这种方法会调整数组中数字的顺序,即会修改输入的数组;
方法1:直接sort排序
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
//排序:
vector<int> res;
sort(arr.begin(), arr.end());
for(int i = 0; i < k; i++) res.push_back(arr[i]);
return res;
}
};
方法2:用大根堆来解决
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
//堆:
vector<int> res;//(k, 0)
//如果k为0,就返回res
if(k == 0) return res;
//(大根)堆:
priority_queue<int> Q;
//先把前k个数入队:
for(int i = 0; i < k; i++)
Q.push(arr[i]);
//从第k+1个数开始遍历:
for(int i = k; i < arr.size(); i++){
//如果arr[i]比堆顶元素小,就把堆顶元素弹出,然后把arr[i]入队,这样就可以使得堆中的元素一定是最小的k个数
if(arr[i] < Q.top()){
Q.pop();
Q.push(arr[i]);
}
}
//把堆中的数给到res容器,并返回:
for(int i = 0; i < k; i++){
res.push_back(Q.top());//res[i] = Q.top();
Q.pop();
}
//或者写成下面几行:
//while(!Q.empty()){
// res.push_back(Q.top());
// Q.pop();
//}
return res;
}
};
上面的程序中堆是用优先队列priority_queue来表示,还可以自己去实现一个堆,程序如下:
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res;
if(k == 0) return res;
//堆排序:只排k个数
HeapSort(arr, k);
//再调整堆:
for(int i = k; i < arr.size(); i++){
if(arr[i] < arr[0]){
swap(arr[i], arr[0]);
adjustHeap(arr, 0, k);
}
}
for(int i = 0; i < k; i++) res.push_back(arr[i]);
return res;
}
private:
void adjustHeap(vector<int>& arr, int root, int len){
//这个函数的作用就是用来使当前root节点的子树符合堆的规律/堆的规则:
//root是某个节点的下标,len是总的结点个数
int left = 2 * root + 1;//左孩子
int right = 2 * root + 2;//右孩子
//大根堆:
int max = root;
if(left < len && arr[left] > arr[max]) //left <= len 防止节点不存在
max = left;
if(right < len && arr[right] > arr[max]) //arr[right] > arr[max] 判断是不是根节点最大(因为你每个子树都要符合大根堆的性质)
max = right;
if(root != max){//确实最大值不是父节点
swap(arr[root], arr[max]);
adjustHeap(arr, max, len);
}
}
void HeapSort(vector<int>& arr, int len){
//初始化建堆:
for(int i = len / 2 - 1; i >= 0; --i)//遍历每个非叶子节点
adjustHeap(arr, i, len);//使每个非叶子节点的子树符合堆的规律
//排序重建堆:
//for(int i = len - 1; i >= 0; --i){
// swap(arr[0], arr[i]);
// adjustHeap(arr, 0, i);
//}
}
};
补充:leetcode上的答案
class Solution {
public:
void adjustHeap(vector<int>& arr, int i, int heapsize){//大顶堆
int l = 2*i+1, r = 2*i+2, maxindex = i;
if(l<heapsize && arr[l]>arr[maxindex])
maxindex = l;
if(r<heapsize && arr[r]>arr[maxindex])
maxindex = r;
if(maxindex != i){
swap(arr[i], arr[maxindex]);
adjustHeap(arr, maxindex, heapsize);
}
}
void buildHeap(vector<int>& arr, int heapsize){
for(int i = (heapsize-1)/2; i>=0; --i){
adjustHeap(arr, i, heapsize);
}
}
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res;
if(k==0) return res;
buildHeap(arr, k);
for(int i = k; i<arr.size(); ++i){
if(arr[i] < arr[0]){
swap(arr[i], arr[0]);
adjustHeap(arr, 0, k);
}
}
for(int i = 0; i<k; ++i){
res.push_back(arr[i]);
}
return res;
}
};
方法3:快排思想(partition函数是一次快排,以最左边的数为参考值)
代码中k指的是下标:
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> res;
if(k == 0) return res;
//快排:
QuickSort(arr, 0, arr.size() - 1, k);
for(int i = 0; i < k; i++) res.push_back(arr[i]);
return res;
}
private:
void QuickSort(vector<int>& arr, int left, int right, int k){
//这行可要可不要,因为这里不是完整的快排,而是只快排前k个数:
if(left >= right) return;
//执行一次快排:
int pos = Partition(arr, left, right);
//pos是下标,表示第pos + 1个数:
if(pos + 1 == k) return;//if(pos == k) return;当一共有10个数,pos为9,k为10时,if(pos == k)就不满足了,所以是if(pos + 1 == k)
else if(pos + 1 > k)
QuickSort(arr, left, pos - 1, k);
else
QuickSort(arr, pos + 1, right, k);
}
int Partition(vector<int>& arr, int left, int right){
//最左边的数作为基准:
int tmp = arr[left];
while(left < right){
while(left < right && arr[right] > tmp) --right;
arr[left] = arr[right];
while(left < right && arr[left] <= tmp) ++left;//这里是<=,不要只写<
arr[right] = arr[left];
}
//这个别忘了!!!
arr[left] = tmp;// arr[high] = tmp;都可以
return left;
//最右边的数作为基准:参数换成了low和high
// int tmp = arr[high];
// while(low < high){
// while(low < high && arr[low] <= tmp) ++low;
// arr[high] = arr[low];
// while(low < high && arr[high] > tmp) --high;
// arr[low] = arr[high];
// }
// arr[high] = tmp;//arr[low] = tmp;都可以
// return low;
}
};
(力扣上的官方答案)这里的k是指个数,上面的一种方法中k指的是下标。
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
srand((unsigned)time(NULL));
randomized_selected(arr, 0, arr.size() - 1, k);
vector<int> res;
for(int i = 0; i < k; i++)
res.push_back(arr[i]);
return res;
}
private:
void randomized_selected(vector<int>& arr, int left, int right, int k){
if(left >= right) return;
//随机生成一个下标:
int pos = randomized_partition(arr, left, right);
//计算下标是第几个下标:
int num = pos - left + 1;
//这里的k是个数:
if(num == k) return;
else if(num > k) randomized_selected(arr, left, pos - 1, k);
else randomized_selected(arr, pos + 1, right, k - num);//所以这里是k - num
}
int randomized_partition(vector<int>& arr, int left, int right){
int i = rand() % (right - left + 1) + left;
swap(arr[right], arr[i]);
return partition(arr, left, right);
}
int partition(vector<int>& nums, int left, int right){
int pivot = nums[right];
int i = left - 1;
for(int j = left; j < right; ++j){
if(nums[j] <= pivot){
++i;
swap(nums[i], nums[j]);
}
}
swap(nums[i + 1], nums[right]);
return i + 1;
}
};
快速排序
书上说的partition函数,是想随机选出一个下标,然后将此下标对应的数和数组最后边的数进行交换,然后以最右边的数为参考值,进行一次快排。
书上的快排算法:
//快速排序:
void QuickSort(int data[], int length, int start, int end){
if(start == end)
return ;
int index = Partition(data, length, start, end);
if(index > start)
QuickSort(data, length, start, index - 1);
if(index < end)
QuickSort(data, length, index + 1, end);
}
//一次快排:
int Partition(int data[], int length, int start, int end){
if(data == nullptr || length <= 0 || start < 0 || end >= length)
return -1;
int index = RandomInRange(start, end);//生成一个在start和end之间的随机数
Swap(&data[index], &data[end]);//交换两个数字
int small = start - 1;
for(index = start; index < end; ++index){
if(data[index] < data[end]){
++small;
if(small != index)
Swap(&data[index], &data[small]);
}
}
++small;
Swap(&data[small], &data[end]);
return small;
}
自己模仿着写的快排:
#include还有一个直接写在一个函数里的快排算法代码:
void QuickSort1(vector<int>& arr, int left, int right){
//若待排序序列只有一个元素,返回空
if(left >= right) return;
int i = left;//i作为指针从左向右扫描
int j = right;//j作为指针从右向左扫描
int tmp = arr[i];//第一个数作为基准数
while(i < j){
int tmp = arr[i];
while(i < j && arr[j] > tmp) --j;//从右边找小于基准数的元素 (此处由于j值可能会变,所以仍需判断i是否小于j)
arr[i] = arr[j];
while(i < j && arr[i] <= tmp) ++i;//从左边找大于基准数的元素
arr[j] = arr[i];
}
arr[i] = tmp;//当i和j相遇,将基准元素赋值到指针i处
int pos = i;
QuickSort1(arr, i, pos - 1);//pos左边的序列继续递归调用快排
QuickSort1(arr, pos + 1, j);//pos右边的序列继续递归调用快排
}
堆排序
参考链接:堆排序——C++实现 和 堆的构建, 以及堆排序的c++实现。
堆排序总共分为两步:
1、初始化建堆:
找到一个树的最后一个非叶节点, 计算公式为 (n-1)/2 -1, 然后遍历树的每个非叶节点,使其符合堆的规则。
2、排序重建堆:
此时 [0, len - 1] 为一个堆 ,将堆的顶部,与最后一个元素交换(swap(arr[0], arr[i]);),此时剩下的元素[0, len - 2] 所组成的树已经不是堆了,所以要将剩下的元素通过 堆调整函数adjustHeap()调整成堆,具体就是adjustHeap(arr, 0, i);。
void adjustHeap(vector<int>& arr, int root, int len){
//这个函数的作用就是用来使当前root节点的子树符合堆的规律/堆的规则:
//root是某个节点的下标,len是总的结点个数
int left = 2 * root + 1;//左孩子
int right = 2 * root + 2;//右孩子
//大根堆:
// int max = root;
// if(left < len && arr[left] > arr[max]) //left <= len 防止节点不存在
// max = left;
// if(right < len && arr[right] > arr[max]) //arr[right] > arr[max] 判断是不是根节点最大(因为你每个子树都要符合大根堆的性质)
// max = right;
// if(root != max){//确实最大值不是父节点
// swap(arr[root], arr[max]);
// adjustHeap(arr, max, len);
// }
//小根堆:
int min = root;
if(left < len && arr[left] < arr[min]) //left <= len 防止节点不存在
min = left;
if(right < len && arr[right] < arr[min]) //arr[right] < arr[min]判断是不是根节点最小(因为你每个子树都要符合小根堆的性质)
min = right;
if(root != min){//确实最小值不是父节点
swap(arr[root], arr[min]);//堆顶元素和末尾元素进行交换
adjustHeap(arr, min, len);//从当前节点开始,调整下面的堆
//这里递归的解释见下面
}
}
void HeapSort(vector<int>& arr, int len){
//初始化建堆:
for(int i = len / 2 - 1; i >= 0; --i)//遍历每个非叶子节点
adjustHeap(arr, i, len);//使每个非叶子节点的子树符合堆的规律
//排序重建堆:
for(int i = len - 1; i >= 0; --i){
swap(arr[0], arr[i]);
adjustHeap(arr, 0, i);
}
}
int main(){
vector<int> arr = {1, 9, 3, 3, -2, 5, 6, 8};
for(int x : arr) cout << x << ", "; cout << endl;//1, 9, 3, 3, -2, 5, 6, 8,
//快速排序:
//QuickSort(arr, 0, arr.size() - 1);
//堆排序:
HeapSort(arr, arr.size());
for(int x : arr) cout << x << ", "; cout << endl;//-2, 1, 3, 3, 5, 6, 8, 9,
return 0;
}
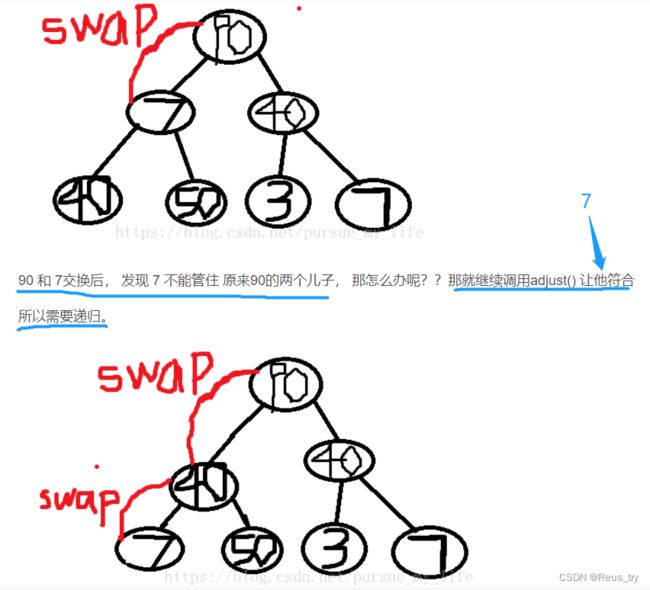
堆调整函数adjustHeap()最后为什么要用递归?
答:
queue deque priority_queued的比较
①大根堆:根的值最大;
②C++ 语言中的堆(即优先队列)为大根堆
③c++中的堆-priority_queue的使用方法:大根堆就是个优先队列priority_queue,用法和队列相似。
vector(单端数组):
vector<int> v;
v.push_back();//尾插
v.pop_back();//尾删
v.front();//首元素
v.back();//最后一个元素
deque(双端数组):
deque<int> d;
d.push_back(num);//尾插
d.pop_back();//尾删
d.push_front(num);// 头插
d.pop_front();//头删
//d.front();//首元素
//d.back();//最后一个元素
stack(栈):
stack<int> st;
st.push(num);//栈顶入栈
st.pop();//栈顶出栈 ——>记得判断是否栈空,栈空之后再出栈会报错
st.top();//返回栈顶元素
queue(队列):
queue<int> q;
q.push(num);//队尾入队
q.pop();//队头出队 ——>记得判断是否队空,队空之后再出队会报错
q.front();//返回队头元素
q.back();//返回队尾元素
priority_queue(优先队列):
//头文件:
#include 面试题41: 数据流中的中位数
难度:困难
先不看
面试题42:连续子数组的最大和(动态规划)
动态规划解析:
状态定义: 设动态规划列表 dp ,dp[i] 代表以元素 nums[i] 为结尾的连续子数组最大和。
为何定义最大和 dp[i] 中必须包含元素 nums[i] :保证 dp[i] 递推到 dp[i+1] 的正确性;如果不包含 nums[i],递推时则不满足题目的 连续子数组 要求。
转移方程: 若 dp[i−1]≤0 ,说明 dp[i−1] 对 dp[i]产生负贡献,即 dp[i−1]+nums[i] 还不如 nums[i] 本身大。
当 dp[i - 1] > 0时:执行 dp[i] = dp[i-1] + nums[i];
当 dp[i−1]≤0 时:执行 dp[i] = nums[i];
初始状态: dp[0] = nums[0],即以 nums[0] 结尾的连续子数组最大和为 nums[0]。
返回值: 返回 dp 列表中的最大值,代表全局最大值。
代码:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
//定义dp数组:
vector<int> dp(n, 0);
dp[0] = nums[0];
int res = nums[0];//如果只有一个数,就返回第一个数
//状态转移:
for(int i = 1; i < n; i++){
if(dp[i - 1] > 0)
dp[i] = dp[i - 1] + nums[i];//与前面相加
else if(dp[i - 1] <= 0) //负贡献
dp[i] = nums[i];//自成一派
if(dp[i] > res) res = dp[i];
}
return res;
}
};
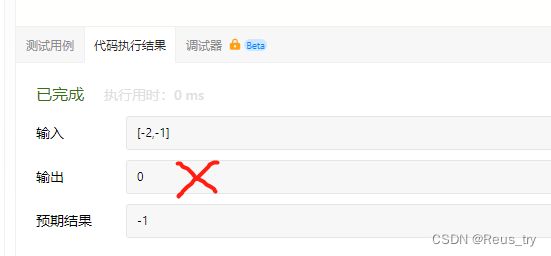
注意:res的初始值只能是nums[0],不能是0:
如果只有一个数,不会进入状态转移的for循环,会直接返回0,结果是错误的;
如果数组是[-2, -1],应该返回-1,如果res初始化为0,会返回0,结果是错误的。
即,如果res初始化为0,如果数组中的元素都是负数,结果就是错误的,因此res的初始值只能是nums[0],不能是0。
面试题43:1~n 整数中 1 出现的次数
难度:困难
先不看
至少要能写出一种常规方法:
class Solution {
public:
int countDigitOne(int n) {
int count = 1;
if(n < 10) return 1;
else{
for(int i = n; i >= 10; --i){
int num = i;
while(num > 0){
if(num % 10 == 1)
++count;
num /= 10;
}
}
}
return count;
}
};
会超出时间限制,因为n的范围:1 <= n < 2^31。
面试题44:数字序列中某一位的数字
更好的方法:(找规律)
先找到是属于几位数的范畴,然后找到是哪个数,再找到是这个数的第几位,把这个数转换成string,结果为str[index] - '0'。
class Solution {
public:
int findNthDigit(int n) {
//一位数单独处理:
if(n < 10) return n;
//
long start = 1;//1位数的第一个数字
long count = 10;//1位数总共有10个数:0-9
int digit = 1;//1位数
while(n > count){
n = n - count;//
start *= 10;
++digit;
count = 9 * start * digit;//
}
//哪一个数?
int target = start + n / digit;
//这个数的哪一位?
int index = n % digit;
//转成string
string str = to_string(target);
//再转成一个数字:
int res = str[index] - '0';
return res;
}
};
注意:start 和 count 要用long型,否则会越界。
常规方法:从0开始注意枚举每个数字,求出该数字是几位数,并把该数字的位数和前面所有数字的位数累加,如果位数之和仍然小于或者等于n,就继续枚举下一个数字;如果累加的数位大于n,那就在当前的数字中找出对应的那一位。
代码:(超出时间限制)n的范围:0 <= n < 2^31
class Solution {
public:
int findNthDigit(int n) {
if(n < 10) return n;
int countSum = 9;
int res;
for(int i = 10; i <= n; ++i){
int tmp = i;
int countNum = getNumCount(i);
countSum += countNum;
if(countSum >= n){
res = getNumICount(tmp, countSum - n + 1);
break;
}
}
return res;
}
private:
int getNumCount(int num){
int count = 0;
while(num){
++count;
num /= 10;
}
return count;
}
int getNumICount(int num, int k){//从右往左数第k位上的数字
int res;
for(int i = 1; i <= k; ++i){
res = num % 10;
num /= 10;
}
return res;
}
};
面试题45:把数组排成最小的数
全排列 面试题38:字符串的排列
这道题不好实现全排列,因为vector中的int位数可能不同,不好拼接成string,拼接好之后也不好比较大小。
这道题是一道排序题,思路如下:
设数组 nums 中任意两数字的字符串为 x 和 y ,则规定 排序判断规则 为:
- 若拼接字符串 x + y > y + x ,则 x “大于” y ;
- 反之,若 x + y < y + x,则 x “小于” y ;
x “小于” y 代表:排序完成后,数组中 x 应在 y 左边;
x “大于” y 代表:排序完成后,数组中 x 应在 y 右边。
本文列举 快速排序 和 内置排序函数 两种排序方法,其他排序方法也可实现。
一、快速排序:
面试题40:最小的K个数后面写了个快速排序,那里是针对int型数组的快速排序,
这道题要写一个针对string型数组的快速排序。
class Solution {
public:
string minNumber(vector<int>& nums) {
//快速排序:
vector<string> v;
for(int x : nums) v.push_back(to_string(x));
QuickSort(v, 0, v.size() - 1);
string res;
for(string str : v) res += str;
return res;
}
private:
void QuickSort(vector<string>& v, int low, int high){
if(low >= high) return;
int pos = Partition(v, low, high);
QuickSort(v, low, pos - 1);
QuickSort(v, pos + 1, high);
}
int Partition(vector<string>& v, int low, int high){
string tmp = v[low];
while(low < high){
while(low < high && v[high] + tmp >= tmp + v[high]) --high;//这里不一样 4 30 > 30 4
v[low] = v[high];
while(low < high && v[low] + tmp <= tmp + v[low]) ++low;//这里不一样 2 30 < 30 2
v[high] = v[low];
}
v[low] = tmp;
return low;
}
};
二、内置排序:(自定义排序规则)
注意:仿函数不能是private,否则会编译出错。
//全局函数实现自定义排序规则(升序):
bool mysort(string a, string b){
if((a + b).compare(b + a) < 0)
return true;
return false;
}
class Solution {
public:
string minNumber(vector<int>& nums) {
vector<string> vec;
for(int i = 0; i < nums.size(); ++i){
vec.push_back(to_string(nums[i]));
}
//sort(vec.begin(), vec.end());//内置的sort函数是升序,但针对的是int数据类型,不是string类型,所以要自定义排序规则
//sort(vec.begin(), vec.end(), mysort);//用全局函数实现
sort(vec.begin(), vec.end(), Solution());//用仿函数实现
//最后把排序后的容器v中的内容拼接成一个完整的串:
string res;
for(string str : vec) res += str;
return res;
}
//private:
//仿函数实现自定义排序规则(升序):
bool operator()(string a, string b){
//用compare函数进行比较:
//if((a + b).compare(b + a) < 0)
// return true;
//return false;
//或者用比较运算符进行比较:
if(a + b < b + a)
return true;
return false;
//或者直接一句代码:
//return a + b < b + a;
}
};
面试题46:把数字翻译成字符串
num为0时的结果是1。
动态规划:

初始状态: dp[0] = dp[1] = 1 ,即 “无数字” 和 “第 11 位数字” 的翻译方法数量均为 11 ;
返回值: dp[n] ,即此数字的翻译方案数量。
Q: 无数字情况 dp[0]=1 从何而来?
A: 当 num 第 1,2 位的组成的数字 ∈[10,25] 时,显然应有 2 种翻译方法,即 dp[2] = dp[1] + dp[0] = 2 ,而显然 dp[1]=1 ,因此推出 dp[0] = 1 。
具体实现:
方法1:把数字num转换成string,然后对字符串进行遍历处理;
方法2:把数字num转换成vector数组,然后对数组进行遍历处理。
方法1:字符串遍历
代码1:
写了个专门用来计算数字num的位数的函数,边界条件是num为0时的情况,需要单独处理。代码2更简洁,也不用单独处理num为0时的情况。
class Solution {
public:
int translateNum(int num) {
//num转换成str:
string str = to_string(num);
//求num的位数:
if(num == 0) return 1;
int n = getNumCount(num);//这样算下来0是0位数,所以要写上面一行单独处理num为0时的情况,因为下面的dp数组长度为1,就不存在dp[1]了,就会出错
//动态规划数字:
vector<int> dp(n + 1);
//初始化:
dp[0] = dp[1] = 1;//如果上面不单独处理num为0时的情况,这里的dp[]的长度为1,那么初始化dp[1]就是错误的
//转移方程:
for(int i = 2; i <= n; ++i){
//第2位数在str中的下标是1,所以是下面这行
int tmp = 10 * (str[i - 2] - '0') + (str[i - 1] - '0');
if(tmp >= 10 && tmp <= 25)//当前位和它的前一位能组成一个在区间[10,25]内的两位数,
dp[i] = dp[i - 1] + dp[i - 2];
else
dp[i] = dp[i - 1];
}
return dp[n];
}
private:
int getNumCount(int num){
int count = 0;
while(num > 0){
++count;
num /= 10;
}
return count;
}
};
代码2:
比较简洁的写法:直接用str.size()来表示数字的位数,这样当num为0时,位数也是1,就不会出现代码1中需要单独处理的情况了。
class Solution {
public:
int translateNum(int num) {
//num转换成str:
string str = to_string(num);
//求num的位数:
int n = str.size();
//动态规划数字:
vector<int> dp(n + 1);
//初始化:
dp[0] = dp[1] = 1;
//转移方程:
for(int i = 2; i <= n; ++i){
//第2位数在str中的下标是1,所以是下面这行
int tmp = 10 * (str[i - 2] - '0') + (str[i - 1] - '0');
if(tmp >= 10 && tmp <= 25)//当前位和它的前一位能组成一个在区间[10,25]内的两位数,
dp[i] = dp[i - 1] + dp[i - 2];
else
dp[i] = dp[i - 1];
}
return dp[n];
}
};
方法2:数字求余
代码:
这种方法就必须要用getNumCount()函数
class Solution {
public:
int translateNum(int num) {
if(num == 0) return 1;
vector<int> v;
int n = getNumCount(num, v);
vector<int> dp(n + 1, 0);
dp[0] = dp[1] = 1;
for(int i = 2; i <= n; ++i){
int tmp = 10 * v[i - 2] + v[i - 1];
if(tmp >= 10 && tmp <= 25)
dp[i] = dp[i - 1] + dp[i - 2];
else
dp[i] = dp[i - 1];
}
return dp[n];
}
private:
int getNumCount(int num, vector<int>& v){
int count = 0;
while(num){
++count;
v.push_back(num % 10);
num /= 10;
}
reverse(v.begin(),v.end());
return count;
}
};
面试题47:礼物的最大价值
代码:
class Solution {
public:
int maxValue(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
//动态规划数组:
vector<vector<int>> dp(rows, vector<int>(cols, 0));
//初始化:
dp[0][0] = grid[0][0];
//第1列:
for(int i = 1; i < rows; ++i) dp[i][0] = grid[i][0] + dp[i - 1][0];
//第1行:
for(int j = 1; j < cols; ++j) dp[0][j] = grid[0][j] + dp[0][j - 1];
//
for(int i = 1; i < rows; ++i){
for(int j = 1; j < cols; ++j){
dp[i][j] = grid[i][j] + max(dp[i - 1][j], dp[i][j - 1]);
}
}
//返回值:
return dp[rows - 1][cols - 1];
}
};
5.3 时间效率与空间效率的平衡
面试题48:最长不含重复字符的子字符串
下面写了好几种方法,直接看最后一种方法吧,滑动窗口+哈希set。(动态规划方法的效率最高)
unordered_set中存的就是每次找到的不重复子串,所以set的长度就是不重复子串的长度,如果比res大,就更新res。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
//哈希集合:
unordered_set<char> buf;//用set hashSet;也可以
int res = 0;//最长不重复子串的长度
int start = 0;//最长不重复子串的左边界,即首字符下标
//遍历整个s:
for(int i = 0; i < s.size(); ++i){
//只要当前元素是第二次出现,就把set中的元素从头开始删,直到把当前元素删掉为止
while(buf.find(s[i]) != buf.end()){
buf.erase(s[start]);//删除set集合中对应字符串s中下标为start的元素,直到把s[i]给删掉
++start;
}
//元素首次出现:就插入到哈希set中
buf.insert(s[i]);
//更新res
if(buf.size() > res)
res = buf.size();
}
return res;
}
};
补充其他的方法:
动态规划+哈希表(这个效率高)
滑动窗口(双指针)+哈希表(这个不好理解)
注意:这道题用哈希表的作用只有一个,就是判断一个字符是否出现过,hashMap.count(s[j])) i = hashMap[s[j]就是没出现过,反之就是出现过。
参考最长不含重复字符的子字符串(C++动态规划+滑窗两种方法):
方法1:动态规划+哈希表:
最长不含重复字符的子字符串,如果用动态规划的方法,我们可以想到用dp[i]表示以第i个字符结尾的不含重复字符的子字符串的最大长度。
那么dp[i]如何通过前面的dp[i-1]递推得到呢?
可以从dp[0]开始,当字符串不为空时,一定可以得到dp[0] = 1。
- 以"abcabcbb"为例,dp[0] = 1;
- 循环判断当前字符是否在前面出现过,这里需要用到哈希表记录前面字符出现过的位置;
- 如果当前字符首次出现,那么dp[i] = dp[i - 1] + 1,比如dp[2] = dp[1] + 1, dp[3] = dp[2] + 1;
- 如果当前字符和哈希表记录的发生重复,计算当前字符位置与前面重复的字符位置的距离
i - j,这里就要分两种情况:
(1)距离i - j > dp[i - 1],即前面重复的那个字符已经不在当前最长非重复子串里面了,比如"abcdeca"中的’a’,我们直接将当前长度在前面的基础上加一即可,因此dp[i] = dp[i - 1] + 1;
(2)i - j <= dp[i - 1], 即前面重复的那个字符包含在当前最长非重复子串里面了,如上面的’c’,我们当前新的最长非重复子串长度应该为i - j,即dp[i] = i - j; - 更新哈希表
- 取
dp中的最大值即为答案。
判断字符是否是首次出现,hashTable.find(s[i]) == hashTable.end() //或者hashMap.count(s[i]) == 0,但是不能写hashMap[s[i]] == 0,因为哈希表中存的是某个元素上次出现的位置下标,而不是出现的次数,前两种写法都可以判断出是否是第一次出现。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.size();
if(n == 0) return 0;
int res = 0;
//动态规划:
vector<int> dp(n, 0);
//哈希表:
unordered_map<char, int> hashTable;
//状态转移:
for(int i = 0; i < n; ++i){
//第1个字符:
if(i == 0)
dp[i] = 1;
//如果字符时首次出现:
else if(hashTable.find(s[i]) == hashTable.end())//hashMap.count(s[i]) == 0,但是不能写hashMap[s[i]] == 0
dp[i] = dp[i - 1] + 1;
//如果字符时第二次出现:
else{//这里写if(hashTable[s[i]] > 0)也可以,因为如果一个字符出现第二次,它的下标最少都是1
int j = hashTable[s[i]];
if(i - j > dp[i - 1])//这里是严格大于,不能是>=
dp[i] = dp[i - 1] + 1;
else
dp[i] = i - j;
}
//更新s[i]最新出现的位置下标:
hashTable[s[i]] = i;//这个别忘了!!!
//更新最大值:
if(dp[i] > res)
res = dp[i];
}
return res;
}
};
//或者这么写:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.size();
if(n == 0) return 0;//空串直接返回0
if(n == 1) return 1;//一个字符的时候直接返回1
//动态规划+哈希表:
unordered_map<char, int> hashMap;
vector<int> dp(n, 0);
//初始化:
dp[0] = 1;
hashMap[s[0]] = 0;//这个别忘了
int res = 0;//如果这里写res = 1,就不需要上面的if(n == 1) return 1;相当于是只要不是空串,res最少为1
for(int i = 1; i < n; ++i){
//首次出现:
if(hashMap.find(s[i]) == hashMap.end())
dp[i] = dp[i - 1] + 1;
else{//第二次出现:
int j = hashMap[s[i]];
if(i - j > dp[i - 1])
dp[i] = dp[i - 1] + 1;
else
dp[i] = i - j;
}
hashMap[s[i]] = i;//这个别忘了!!!
if(dp[i] > res)
res = dp[i];
}
return res;
}
};
方法2:滑动窗口 + 哈希表:
利用滑动窗口也可以方便的解决这个问题,思路类似上面的解法,利用双指针start和i,i用来遍历整个字符串,
初始时start = -1,向右遍历字符串,
如果没有遇到重复的字符,则不含重复字符的子字符串的长度就为i - start,一直增加。
当出现和前面重复的字符时,判断start和之前重复字符的索引大小hashTable[s[i]],然后进行移动,将start指针移到max(hashTable[s[i]], left)的位置,每次遇到重复的字符时,start都要更新。
用unordered_map实现:char是字符,int是字符char的下标
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.size();
if(n == 0) return 0;
unordered_map<char, int> hashTable;
int left = -1;
int res = 0, tmp = 0;
for(int i = 0; i < n; ++i){
//如果是第一次出现:
if(hashTable.find(s[i]) == hashTable.end()){
tmp = i - left;
}
//第二次出现:
else{
left = max(hashTable[s[i]], left);//不是hashTable[s[i]];
tmp = i - left;
}
hashTable[s[i]] = i;
if(tmp > res)
res = tmp;
}
return res;
}
};
//或者这么写:
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int n = s.size();
if(n == 0) return 0;
//if(n == 1) return 1;
//滑动窗口+哈希表:
unordered_map<char, int> hashMap;
int left = -1;
int res = 0, tmp = 0;
for(int i = 0; i < n; ++i){
//如果一个字符重复出现:
if(hashMap.find(s[i]) != hashMap.end()){
left = max(left, hashMap[s[i]]);
}
hashMap[s[i]] = i;
int tmp = i - left;
if(tmp > res) res = tmp;
}
return res;
}
};
用unordered_set实现:
我们可以使用「滑动窗口」来解决这个问题:
我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表着「枚举子串的起始位置」,而右指针为不包含重复字符的最长子串的结束位置 ;
右指针遇到重复字符时,左指针跳到子串里第一个重复字符的位置,并且set把子串中重复字符前的字符去掉,重新右指针再往右扩展;
所以说unordered_set中存的就是每次找到的不重复子串,所以set的长度就是不重复子串的长度,如果比res大,就更新res。
判断重复字符:
在上面的流程中,我们还需要使用一种数据结构来判断 是否有重复的字符,常用的数据结构为哈希集合(即 C++ 中的 std::unordered_set。在左指针向右移动的时候,我们从哈希集合中移除一个字符,在右指针向右移动的时候,我们往哈希集合中添加一个字符。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
//哈希集合:
unordered_set<char> buf;
int res = 0;//最长不重复子串的长度
int start = 0;//最长不重复子串的左边界
//遍历整个s:
for(int i = 0; i < s.size(); ++i){
//元素第二次出现:就把set中的元素挨个删除,直到s[i]被删,这样set中就没有s[i]了,下面再把这个元素插入集合中
while(buf.find(s[i]) != buf.end()){
buf.erase(s[start]);
++start;
}
//元素首次出现:就插入到哈希set中
buf.insert(s[i]);
//更新res
if(buf.size() > res)
res = buf.size();
}
return res;
}
};
面试题49:丑数
方法1:小根堆(优先队列)+手动去重 -->先存后排 (效率很低)
方法2:直接用set实现排序+去重 -->先存后排 (效率很低)
方法3:动态规划 (三指针) -->先排再存 (效率高)
推荐用方法2,然后是方法3,最后是方法1。
补充知识:
优先队列+小根堆–>c++优先队列(priority_queue)用法详解 和 优先队列详解/C++ 和 优先队列(priority_queue)的原理及用法。
在优先队列中,优先级高的元素先出队列,并非按照先进先出的要求,类似一个堆(heap)。
头文件#include :
| 大根堆 | 小根堆 | |
|---|---|---|
| 表示方法 | priority_queue 等同于priority_queue |
priority_queue |
| 队头元素 | top()返回的是最大值 | top()返回的是最小值 |
| 排序 | 数据从小到大排列 | 数据从大到小排列 |
基本操作有:
- empty( ) //判断一个队列是否为空
- pop( ) //删除队顶元素
- push( ) //加入一个元素
- size( ) //返回优先队列中拥有的元素个数
- top( ) //返回优先队列的队顶元素
以下的两种方法参考链接:暴力+优先队列(小顶堆)+动态规划(三指针)。
方法1:
小根堆(优先队列)+手动去重–>先存后排
思路:
利用优先队列有自动排序的功能;
每次取出队头元素,存入队头元素*2、队头元素*3、队头元素*5;
注意:像 12 这个元素,可由 4 乘 3 得到,也可由 6 乘 2 得到,所以要注意去重,这里采用 set 来识别有无重复。
①用小根堆排序,手动去重:先存到priority_queue中然后取队顶元素
class Solution {
public:
int nthUglyNumber(int n) {
//小根堆:
priority_queue<double, vector<double>, greater<double>> q;
double res = 1;//第1个数
for(int i = 1; i < n; ++i){
q.push(res * 2);
q.push(res * 3);
q.push(res * 5);
res = q.top();//队顶元素是队中最小的元素,这样就不会遗漏掉某个丑数
q.pop();//记得把队顶元素出队
//去重:如果q中队顶元素依然等于res,就出队,这样就可以去重
while(!q.empty() && res == q.top()) q.pop();
}
return res;
}
};
②用小根堆排序,用set去重:(这个不太好写)
class Solution {
public:
int nthUglyNumber(int n) {
//小根堆:
priority_queue<double, vector<double>, greater<double>> q;
//set集合:(去重用的)
set<double> s;
//每次都要用当前最小的丑数乘以2 3 5
vector<int> mask = {2, 3, 5};
s.insert(1);
double res = 1;//第1个数
for(int i = 1; i < n; ++i){
for(int j : mask){
//res * j 如果不在set中,再入queue,入set,否则就不管了,这样就可以达到去重的效果
if(s.find(res * j) == s.end()){//s.count(res * j) == 0//
q.push(res * j);
s.insert(res * j);
}
}
//每次取queue队顶元素出来,让它分别乘2 3 5
res = q.top();//队顶元素是队中最小的元素,这样就不会遗漏掉某个丑数
q.pop();//记得把队顶元素出队
}
return res;
}
};
方法2:(方法1的升级版,更简洁)
直接用set来完成排序和去重:先存到set中然后取首元素
class Solution {
public:
int nthUglyNumber(int n) {
//set容器既能去重,也能排序:
set<double> s;
double res = 1;//第1个res,下面再计算n-1个res即可
for(int i = 1; i < n; ++i){
s.insert(res * 2);
s.insert(res * 3);
s.insert(res * 5);
//取set的首元素为res,并且从set中把首元素删除掉
res = *s.begin();
s.erase(res);
}
return res;
}
};
//或者这么写:这种写法看着就不太像是先存后排了
class Solution {
public:
int getUglyNumber(int n) {
//set集合实现排序+去重:
set<double> s;
s.insert(1);
double res;
for(int i = 0; i < n; ++i){
res = *s.begin();
s.erase(res);
s.insert(res * 2);
s.insert(res * 3);
s.insert(res * 5);
}
return res;
}
};
方法3:
动态规划 (三指针) -->先排再存
思路:
我们先模拟手写丑数的过程
1 打头,1 乘 2 1 乘 3 1 乘 5,现在是 {1,2,3,5}
轮到 2,2 乘 2 2 乘 3 2 乘 5,现在是 {1,2,3,4,5,6,10}
手写的过程和采用小顶堆的方法很像,但是怎么做到提前排序呢?
小顶堆的方法是先存再排,dp 的方法则是先排再存;
我们设 3 个指针 ptr2, ptr3, ptr5
代表的是第几个数的2倍、第几个数 3 倍、第几个数 5 倍
动态方程 dp[i] = min(min(num2, num3), num5);
小顶堆是一个元素出来然后存 3 个元素
动态规划则是标识 3 个元素,通过比较他们的 2 倍、3 倍、5 倍的大小,来一个一个存
代码:
class Solution {
public:
int nthUglyNumber(int n) {
//动态规划:
vector<int> dp(n);
//初始化:
dp[0] = 1;
//三个指针:
int ptr2, ptr3, ptr5;//第ptr2个数的2倍,第ptr3个数的3倍,第ptr5个数的5倍
ptr2 = ptr3 = ptr5 = 0;//初始值都是第0个数
for(int i = 1; i < n; ++i){
int num2 = 2 * dp[ptr2];
int num3 = 3 * dp[ptr3];
int num5 = 5 * dp[ptr5];
dp[i] = min(min(num2, num3), num5);
if(dp[i] == num2) ++ptr2;
if(dp[i] == num3) ++ptr3;
if(dp[i] == num5) ++ptr5;
}
return dp[n - 1];
}
};
下面的几个补充是帮助理解动态规划思想的:
补充1:
那个动态规划法,我觉得换一种解释能更清晰一点儿:
相当于3个数组,分别是能被2、3、5整除的递增数组,且每个数组的第一个数都为1;
然后就简单了,维护三个指针,将三个数组合并为一个严格递增的数组。就是传统的双指针法,只是这题是三个指针;
然后优化一下,不要一下子列出这3个数组,因为并不知道数组预先算出多少合适;
这样就一边移指针,一边算各个数组的下一个数,一边merge,就变成了题解的动态规划法的代码。
补充2:
下一次寻找丑数时,则对这三个位置分别尝试使用一次乘2机会,乘3机会,乘5机会,看看哪个最小,最小的那个就是下一个丑数。最后,得到下一个丑数的指针位置加一,因为它对应的那次乘法使用完了。
这里需要注意下去重的问题,如果某次寻找丑数,找到了下一个丑数10,则pointer2和pointer5都需要加一,因为5乘2等于10, 2乘5也等于10,这样可以确保10只被数一次。
补充3:
三指针方法的理解方式:(见链接)
官方题解里提到的三个指针p2,p3,p5,但是没有说明其含义,实际上pi的含义是有资格同i相乘的最小丑数的位置。这里资格指的是:如果一个丑数nums[pi]通过乘以i可以得到下一个丑数,那么这个丑数nums[pi]就永远失去了同i相乘的资格(没有必要再乘了),我们把pi++让nums[pi]指向下一个丑数即可。
不懂的话举例说明:
一开始,丑数只有{1},1可以同2,3,5相乘,取最小的1×2=2添加到丑数序列中。
现在丑数中有{1,2},在上一步中,1已经同2相乘过了,所以今后没必要再比较1×2了,我们说1失去了同2相乘的资格。
现在1有与3,5相乘的资格,2有与2,3,5相乘的资格,但是2×3和2×5是没必要比较的,因为有比它更小的1可以同3,5相乘,所以我们只需要比较1×3,1×5,2×2。
依此类推,每次我们都分别比较有资格同2,3,5相乘的最小丑数,选择最小的那个作为下一个丑数,假设选择到的这个丑数是同i(i=2,3,5)相乘得到的,所以它失去了同i相乘的资格,把对应的pi++,让pi指向下一个丑数即可。
补充:归并排序(分治 + 递归)
LeetCode刷题1:☆☆☆力扣912题:排序算法 中的 ⑥归并排序(分治 + 递归)
1.Merge()中
要新建一个临时数组,把左右两部分的按从小到大的顺序存进来,然后再存回到原来数组的[low, high]区间;
2.MergeSort()中
mid是数组的中间位置,左右两部分分别是闭区间的[low, mid]和[mid + 1, high]。
代码:
#include面试题50:字符串中第一个只出现一次的字符
思路:哈希表实现(遍历s创建哈希表,然后再遍历s)
class Solution {
public:
char firstUniqChar(string s) {
unordered_map<char, int> hashTable;
char res;
bool flag = false;
//遍历s:
for(int i = 0; i < s.size(); ++i){
++hashTable[s[i]];
}
//再次遍历s:
for(int i = 0; i < s.size(); ++i){
if(hashTable[s[i]] == 1){
res = s[i];
flag = true;
break;
}
}
if(flag)
return res;
return ' ';
}
};
//简洁一点的写法:
class Solution {
public:
char firstUniqChar(string s) {
class Solution {
public:
char firstUniqChar(string s) {
unordered_map<char, int> hashTable;
for(int i = 0; i < s.size(); ++i){
++hashTable[s[i]];
}
for(int i = 0; i < s.size(); ++i){//
if(hashTable[s[i]] == 1)
return s[i];
}
return ' ';
}
};
//更简洁的写法:
class Solution {
public:
char firstUniqChar(string s) {
int n = s.size();
//哈希表:
unordered_map<char, int> hashMap;
for(char& ch : s) ++hashMap[ch];
for(char& ch : s){
if(hashMap[ch] == 1)
return ch;
}
return ' ';
}
};
这里有个问题,如果我直接遍历hashTable,结果不对:
class Solution {
public:
char firstUniqChar(string s) {
//if(s.size() == 0) return ' ';
unordered_map<char, int> hashTable;
char res;
bool flag = false;
for(int i = 0; i < s.size(); ++i){
++hashTable[s[i]];
}
//for(int i = 0; i < s.size(); ++i){//
//if(hashTable[s[i]] == 1){//
for(auto it = hashTable.begin(); it != hashTable.end(); ++it){
//cout << it->first << ", ";//输出
if(it->second == 1){
res = it->first;//
flag = true;
break;
}
}
if(flag)
return res;
return ' ';
}
};
结果是:
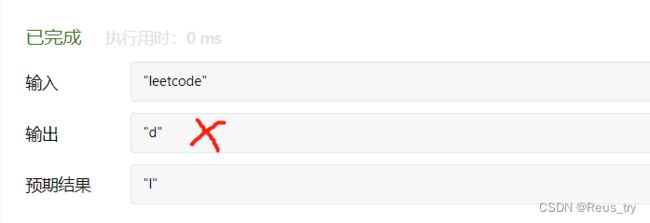
然后我把hashTable中的内容输出,发现是反的:
for(auto it = hashTable.begin(); it != hashTable.end(); ++it){
cout << it->first << ", ";
}
结果是d, o, c, t, e, l, ,而不是预期的l, e, t, c, o, d, ,这块再查一下是什么原因(???)
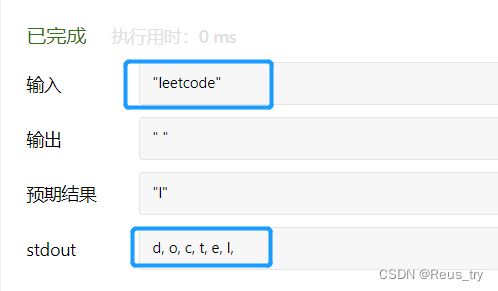
原因:
map 和 unordered_map的比较:
- map: map内部实现了一个红黑树(不严格平衡的二叉排序树),该结构具有自动排序的功能,因此map内部的所有元素都是有序的;
- unordered_map: unordered_map内部实现了一个哈希表,因此其元素的排列顺序是杂乱的,无序的。
所以不能通过遍历hashTable来找出现次数为1的元素。
相关题目:
补充:c++ unordered_map 3种遍历方式
链接:点这里
先创建一个unordered_map:
unordered_map<int,int> map={
pair<int,int>(1,2),
pair<int,int>(3,4)
};
方式一:值传递遍历
for(pair<int,int> kv:map){
cout<<kv.first<<kv.second<<endl;
}
//使用auto:
for(auto kv:map){
cout<<kv.first<<kv.second<<endl;
}
方式二:引用传递遍历
注意:要加const
for(const pair<int,int>& kv:map){
cout<<kv.first<<kv.second<<endl;
}
//使用auto:
for(auto& kv:map){
cout<<kv.first<<kv.second<<endl;
}
方式三:使用迭代器遍历
for(unordered_map<int,int>::iterator it=map.begin();it!=map.end();it++){
cout<<it->first<<it->second<<endl;
}
//使用auto:
for(auto it=map.begin();it!=map.end();it++){
cout<<it->first<<it->second<<endl;
}
面试题50’:字符流中第一个只出现一次的字符
题目:
请实现一个函数用来找出字符流中第一个只出现一次的字符。
例如,当从字符流中只读出前两个字符 go 时,第一个只出现一次的字符是 g。
当从该字符流中读出前六个字符 google 时,第一个只出现一次的字符是 l。
如果当前字符流没有存在出现一次的字符,返回 # 字符。
样例
- 输入:“google”
- 输出:“ggg#ll”
解释:每当字符流读入一个字符,就进行一次判断并输出当前的第一个只出现一次的字符。
思路:
哈希表只统计每个字符出现的次数,队列中只存首次出现的字符,出现次数大于1次的出队,并且再也不会入队。
代码:
class Solution{
unordered_map<char, int> hashTable;
queue<char> q;
public:
//Insert one char from stringstream
void insert(char ch){
//如果字符ch是首次出现,就入队,否则不入队:
if(hashTable.find(ch) == hashTable.end())//hashTable[ch] == 0 //hashMap.count(ch) == 0
q.push(ch);
++hashTable[ch];
}
//return the first appearence once char in current stringstream
char firstAppearingOnce(){
//遍历队列,如果队头元素出现次数大于1,就出队,并且不会再入队了
while(!q.empty() && hashTable[q.front()] > 1)
q.pop();
if(q.empty())
return '#';//队空就返回'#':
return q.front();//否则返回队头元素
}
};
注意:队头元素是q.front(),不是q.top()。
面试题51:数组中的逆序对
等级:困难
先不做了。
面试题52:两个链表的第一个公共结点

问题1:在示例1中为什么1不是交点?
答:看看示例1前面那个图 和示例1图, 只是两个节点的val值都为1罢了,一个节点是a2,一个节点b3, 并不是同一个节点 ,相同的节点是c1。
就好像两个人名字一样,长得不一样,住的地方也不一样
问题2:HashSet不是不能重复吗 ? 万一链表里有值相同的节点呢
答:hashset存的是node的ListNode *,哪怕相同val的node,ListNode *值还是不同的。
下面介绍两种方法:其中方法2的效率更高
方法1:哈希集合(空间复杂度为链表A的长度)
首先遍历链表 headA,并将链表 headA 中的每个节点加入哈希集合中;
然后遍历链表 headB,对于遍历到的每个节点,判断该节点是否在哈希集合中:
- 如果当前节点不在哈希集合中,则继续遍历下一个节点;
- 如果当前节点在哈希集合中,则后面的节点都在哈希集合中,即从当前节点开始的所有节点都是两个链表的公共节点,因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表的第一个公共节点,返回该节点。
如果链表 headB 中的所有节点都不在哈希集合中,则两个链表不相交,返回 null。
方法2:双指针法(可以将空间复杂度降至 O(1))
只有当链表 headA 和 headB 都不为空时,两个链表才可能相交。因此:
首先判断两个链表是否为空,如果其中至少有一个链表为空,则两个链表一定不相交,返回null。
当链表 headA 和 headB 都不为空时,创建两个指针 pA 和 pB,初始时分别指向两个链表的头节点 headA 和 headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:
每步操作需要同时更新指针 pA 和 pB。
如果指针 pA 不为空,则将指针 pA 移到下一个节点;
如果指针 pB 不为空,则将指针 pB 移到下一个节点。
如果指针 pA 为空,则将指针 pA 移到链表 headB 的头节点;
如果指针 pB 为空,则将指针 pB 移到链表 headA 的头节点。
当指针 pA 和 pB 指向同一个节点或者都为空时,返回它们指向的节点或者 null。
代码1:哈希集合
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
//哈希集合:
unordered_set<ListNode*> hashSet;
ListNode* cur = headA;
while(cur){
hashSet.insert(cur);
cur = cur->next;
}
cur = headB;
while(cur){
if(hashSet.count(cur) != 0)//hashSet.find(cur) != hashSet.end()
return cur;
cur = cur->next;
}
return NULL;
}
};
代码2:双指针法
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
//双指针法:
ListNode* pA = headA;
ListNode* pB = headB;
//有一个为空:
if(pA == NULL || pB == NULL) return NULL;
//都非空:
while(pA != pB){
if(pA)
pA = pA->next;
else
pA = headB;
if(pB)
pB = pB->next;
else
pB = headA;
}
return pA;
}
};
//更简洁的写法:
class Solution {
public:
ListNode *findFirstCommonNode(ListNode *headA, ListNode *headB) {
if(headA == NULL || headB == NULL) return NULL;
ListNode* pA = headA;
ListNode* pB = headB;
while(pA != pB){
pA = (pA == NULL) ? headB : pA->next;
pB = (pB == NULL) ? headA : pB->next;
}
return pA;
}
};
第6章 面试中的各项能力
点这里