Leetcode刷题笔记 2021-6-26更新

动态规划

354.俄罗斯套娃

解题思路在于，将数组的其中一维从小到大排列，从而固定一维，把问题简化到找出另一维中的最长递增序列。

思路一

依次遍历第二维的序列，令$f(i)$为序列前i个数字中的最长递增序列的长度，则有$f(i)=ma{x}_{j<i,h[j]<h[i]}f(j)+1$.

for (i = 1; i < m; ++i)
        {
            for (j = 0; j < i; ++j)
            {
                if (envelopes[i][1] > envelopes[j][1])dp[i] = max(dp[i], dp[j] + 1);
            }
        }

这个算法需要两次遍历数组的其中一维，因此时间复杂度为$O(n^2)$.

trick1: sort()函数

sort(envelopes.begin(), envelopes.end(), [](const auto& left, const auto& right) 
            {
                return left[0] == right[0] ? left[1] > right[1]:left[0] < right[0];
            }
            );

trick2: max_element()

*max_element(dp.begin(), dp.end());

返回vector中最大的字符，不加*返回的是迭代器。

思路二

设$f(i)$为长度为$i$的递增序列中最小的末尾值，因此当从前往后遍历数组的第二维数据，当遍历到的$h[j]$大于$f(i)$时，可将$h[j]$直接添加到已存在的最长递增序列之后，从而最长递增序列的长度由$j$变为$j+1$。
而当遍历到的$h[j]$小于或等于$f(i)$时，则在$f(k),k<i$中找到某个值$k_0$，使得$f(k_0)$为小于$h[j]$的$f(k)$中的最大值，即:
$f(k_0)<h[j]<=f(k_0+1)$
如果找到了该值$f(k_0)$，则说明可更新:
$f(k_0+1)=min(f(k_0+1),h[j])$.
该算法在查找$f(k_0)$时使用了查找有序序列值最快的二分查找，从而使得算法复杂度变为$O(nlogn)$.

trick1: lower_bound()

二分查找有如下三个函数：
lower_bound(起始地址，结束地址，要查找的数值) 返回的是数值第一个次出现的位置。
upper_bound(起始地址，结束地址，要查找的数值) 返回的是第一个大于待查找数值出现的位置。
binary_search(起始地址，结束地址，要查找的数值) 返回的是是否存在这么一个数，是一个bool值。

338.比特位计数

思路一

$y=x\&(x-1)$得到的$y$的二进制数为将$x$的二进制数的最后一个1转换为0，即$y$的1要比$x$的1少一个，因此可以使用动态规划：
令$f(x)$为数字x的二进制序列中1的个数，则有
$f(x)=f(x\&(x-1))+1$

trick1: $x\&(x-1)$

思路二

记录那些2的次方的数字，这类数字的特点为$x\&(x-1)=0$. 设某个数字n，有$2^i<n<2^{i+1}$，则$f(n)=f(n-2^i)+1$，时间复杂度为$O(n)$.

32.最长有效括号

思路一

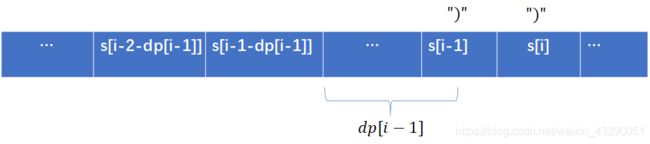
使用动态规划的思想，设下标为$i$的子串的总的最长有效括号长度为$dp[i]$，则可以得知，当$s[i]==‘(’$时，$dp[i]=0$;而当$s[i]={=}^{\prime }{)}^{\prime }$时，则需要分情况讨论：
1.若$s[i-1]={=}^{\prime }{(}^{\prime }$，则有$dp[i]=dp[i-2]+2$
2.若$s[i-1]={=}^{\prime }{)}^{\prime }$，则如果满足$s[i-1-dp[i-1]]={=}^{\prime }{(}^{\prime }$，则有$dp[i]=dp[i-1]+dp[i-2-dp[i-1]]+2$.

115.不同的子序列

用$dp[i][j]$来表示$s[i:]$中的$t[j:]$个数，$s[i:]$，$t[j:]$分别表示$s$和$t$两个字符串中，以下标$i,j$为起点到两字符串末尾的子字符串。
当$s[i]==t[j]$时，$dp[i][j]=dp[i+1][j+1]+dp[i+1][j]$，而当$s[i]!=t[j]$时，$dp[i][j]=dp[i+1][j]$.

152.乘积最大子数组

动态规划，分别计算以i为下标的最大与最小连续子串的乘积：
因为遍历到的数字有可能为负数，假如nums[i]为负数，则求以i结尾的最大连续子串乘积就可以为以i-1结尾的最小连续子串乘积再乘以nums[i]。

if(nums[i]>0)
 {
     dpmax[i]=max(dpmax[i-1]*nums[i],nums[i]);
     dpmin[i]=min(dpmin[i-1]*nums[i],nums[i]);
 }
 else if(nums[i]<0)
 {
     dpmax[i]=max(dpmin[i-1]*nums[i],nums[i]);
     dpmin[i]=min(dpmax[i-1]*nums[i],nums[i]);
 }
 else
 {
     dpmax[i]=dpmin[i]=0;
 }

322.零钱兑换

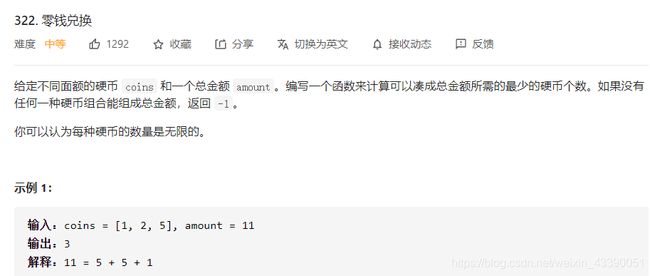
$dp[i]$表示凑成i需要的最小数额
转移方程：
$dp[i]=min\left\{dp[i-c_0],dp[i-c_1],...,dp[i-c_k]\right\}$
$k$为coins的数量。

877.石子游戏

https://leetcode-cn.com/problems/stone-game/

树形动态规划

337.打家劫舍3

树形动态规划可以采用哈希表的方式存储树节点与值。

双指针

15.三数之和

思路一

首先将数据进行从小到大排列，并设置三个指针，$i$指针依次遍历序列，而$j$指针从每次$i+1$开始，$k$指针每次从序列末尾，即$n-1$开始。每当$i,j,k$三个指针所指的数字相加大于0时，则说明$k$指针太大，作$k-1$操作；同理若之和小于0，则说明$j$太小，作$j+1$操作。
本题难度在于如何去重。每次在作为$nums[i]+nums[j]+nums[k]$与0的关系之后，对相应的指针进行移动时，需判断该指针所指的数字与下一个位置的数字是否相同，例如判断$nums[j]?=nums[j+1]$或者$nums[k]?=nums[k-1]$，如果等于，则指针需继续往下一个位置移动。

 if (sum > 0)
 	{
 		while (j<k&&nums[k] == nums[k - 1])k--;
        k--;
    }
 else if (sum < 0)
    {
        while (j<k&&nums[j] == nums[j + 1])j++;
        j++;
    }
 else
    {
        res.push_back({ nums[i],nums[j],nums[k] });
        while (j<k&&nums[j] == nums[j + 1])j++;
        while (j<k&&nums[k] == nums[k - 1])k--;
        j++;
        k--;
    }

160.相交链表

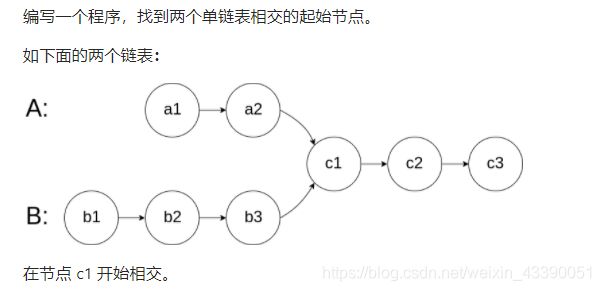
设置两个i，j指针，分别从A，B头指针开始往后遍历。当i指针遍历到A尾部时，将i返回到B的头指针继续遍历；当j指针遍历到B尾部时，将j返回到A头指针继续遍历，当i，j相等时，即为相交节点。

142.环形链表

设置快慢指针，慢指针每次走一步，快指针每次走两步，如图所示：

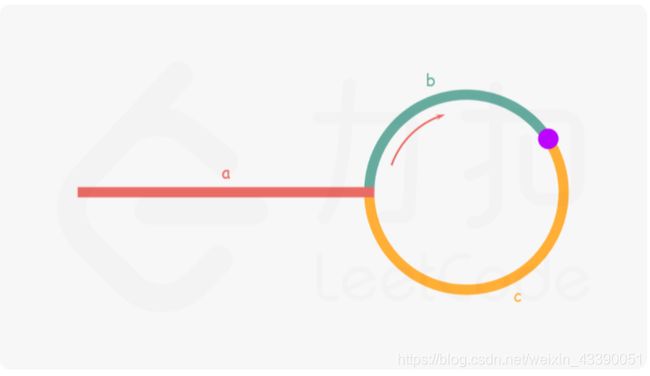
则当他们在环中相遇时：
慢指针走的步数为：$k=a+b$
快指针走的步数为：$2k=a+(n+1)b+nc$
则有：$2k=2a+2b$
$a=(n-1)b+nc=(n-1)(b+c)+c$
因此从相遇点到入环点的距离就等于从头部到入环点的距离，因此可以设置两个指针分别从相遇点和头部往后走，相遇时即为入环点。

287.寻找重复数

构建映射关系：
0->nums[0]=1;
1->nums[1]=3;
3->nums[3]=2;
2->nums[2]=4;
4->nums[4]=2;
即生成了一个1->3->2->4->2带环的链表，从而就可以用142题的环形链表找环的入口来解。

回溯算法

回溯算法可以看作是建立一棵二叉树，使用深度优先遍历，当遍历到某个结点走不通时，则返回该节点的父结点，并继续判断兄弟结点。

131.分割回文串

判断是否为回文串，可以使用动态规划的方法，即判断$dp[i][j]=dp[i+1][j-1]\&\&(s[i]==s[j])$，而对于遍历所有可能，则可建立二叉树，以“aab”为例，如图所示。

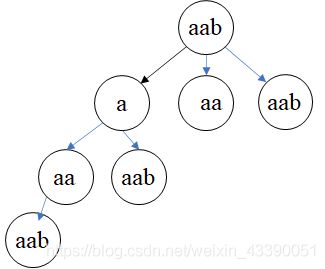
具体代码实现为：

auto dfs(string s,int i)
    {
        if (i == n) {
            res.push_back(temp);
            return;
        }
        int j;
        for (j = i; j < n; ++j)
        {
            if (dp[i][j])
            {
                temp.push_back(s.substr(i, j - i + 1));
                dfs(s, j + 1);
                temp.pop_back();
            }
        }
    }

46.全排列

这道题最简单的思路便是用深度优先算法遍历，并且遍历的过程中，需要判断该元素是否已被遍历，最简单的想法是设立一个记录数组，但这样会造成空间和搜寻时间的增加。
而全排列官方讲解中提出了一种不需要多余空间的回溯算法。

单调栈：寻找下一个更大/最小元素

503.下一个更大元素

解释见：503.下一个更大元素

42.接雨水

采用单调栈的思想，相当于找寻下一个比当前栈顶元素大的值。
动画演示：42.接雨水_单调栈动画演示

456.132模式

这道题维护一个从栈顶到栈底依次减小的单调栈，从后往前遍历。并且记录下右边最大的可以当作2的值。
每当遍历到一个数字时，首先判断其是否小于已保存的2的值，若小于，则返回true，否则继续判断其是否大于栈顶元素，如果大于，则将其入单调栈，且更新2的值为最后一个小于该元素的栈顶元素，此时2的含义即为最大小于该元素的数字。
若小于，则将其入栈，并且不做其他操作。

 tmp2 = INT_MIN;
        for (i = n - 2; i >= 0; --i)
        {
            if (nums[i] < tmp2)return true;
            if (nums[i] > s.top())
            {
                while (!s.empty() && nums[i] > s.top())
                {
                    tmp2 = s.top();
                    s.pop();
                }
            }
            s.push(nums[i]);
        }

84.柱状图中最大的矩形

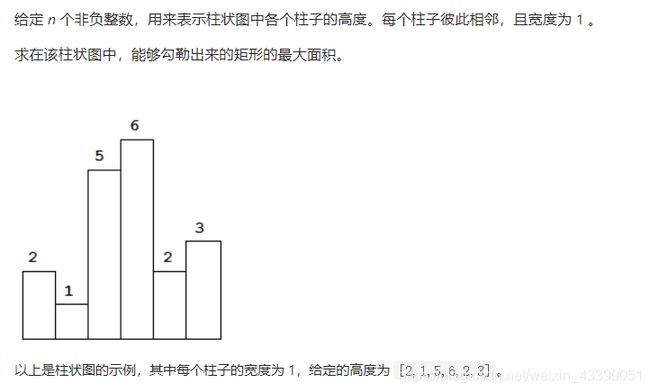
从左往右遍历，维护一个从单调递增的单调栈，即栈底元素到栈顶元素单调递增。每当入一个比栈顶元素小的元素时，则栈顶元素出栈，且以栈顶元素为高的长方形的面积就等于栈顶元素左边连续大于等于其高度的长方形数量$n_{left}$，再乘以其高度$height[s.top().first]$，再加上右边（包括自身）大于等于其高度的长方形数量$n_{right}$，再乘以其高度，因此以当前栈顶所在长方形为高的最大面积为：
$S=(n_{left}+n_{right})\ast height[s.top().first]$
可以求得$n_{right}=i-s.top()$
而对于$n_{left}$，则在元素入栈时记录。当元素入栈时，若栈为空，则说明该元素为目前遍历到此最小元素，因此$n_{left}=i$，而若栈不空，则$n_{left}=i-s.top()-1$

stack<pair<int,int>>s;
for(int i=0;i<m+1;++i)
{
	count=0;
    while(!s.empty()&&heights[i]<heights[s.top().first])
    	{
        	res=max(res,heights[s.top().first]*(i-s.top().first)+s.top().second);
            s.pop();
        }
        if(!s.empty())count=(i-s.top().first-1)*heights[i];
        else count=i*heights[i];
        s.emplace(i,count);
}

85.最大矩形

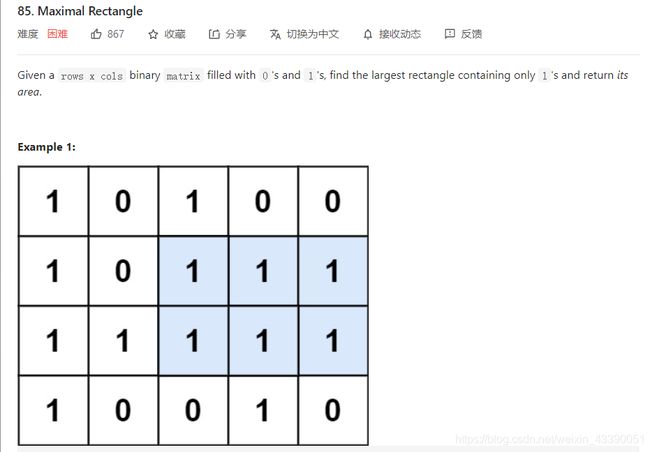
此题如果从矩阵第一行依次往下遍历，以每一行为底，上面的矩形为高，则该题本质上就转换成了第84题。

栈

224.基本计算器+,-,()

实现一个简单计算器来计算简单字符串s的值：

思路一

设置两个栈，一个用来存储运算符，另一个则存储数字，依次遍历s的每个字符。

1. 当遍历到的字符为数字时，需要判断 ：①此时该数字是否为多位数，即遍历到的$s[i]$的后面一个或几个是否也是数字，如果是，则需要将完整的整数提取出来。 ②在得到完整的数字后，需判断操作符栈的栈顶操作符，如果为+或者-，则需要将该数字与数字栈顶的数字作相应的+或-操作，再将得到的结果入数字栈中。

2. 当遍历到的字符为“）”时，此时栈顶的元素一定为“(”，因此将“（”出栈，同时此时要判断操作符栈的栈顶是否为运算符，若是则需要从数字栈中取栈顶两个数字进行运算。因为运算符栈中不可能有两个运算符+或-相邻，因此在(出栈之后，只需判断一次运算符栈顶元素

3. 当遍历到其他运算符时，则直接入运算符栈。

思路二

由于题目中只考虑+，-以及括号，因此将括号全部取消后，不会影响运算优先级，只会可能对某些运算符产生影响。设置一个符号栈，用于存储碰到‘（’时的符号。设置sign表示当前符号，初始为1.

1. 当遇到减号，则$sign=-sign$
2. 若遇到加号，$sign=sign$
3. 若遇到（，则当前sign入栈
4. 若遇到 )，则sign栈顶元素出栈

 sign.push(1);
 sig = 1;
 while (i < n)
        {
            if (s[i] == '(')
                sign.push(sig);
            else if (s[i] == ')')
                sign.pop();
            else if (s[i] == '-')
                sig = -sign.top();
            else if (s[i] == '+')
                sig = sign.top();
            else if (s[i] >= 48 && s[i] <= 58)
            {
                int num = 0;
                while (i<n&&s[i] >= 48) { num = 10 * num + s[i] - 48; ++i; }
                i--;
                res = res + sig * num;
            }
            ++i;
        }

链表

23.合并K个升序链表

思路一：分治递归

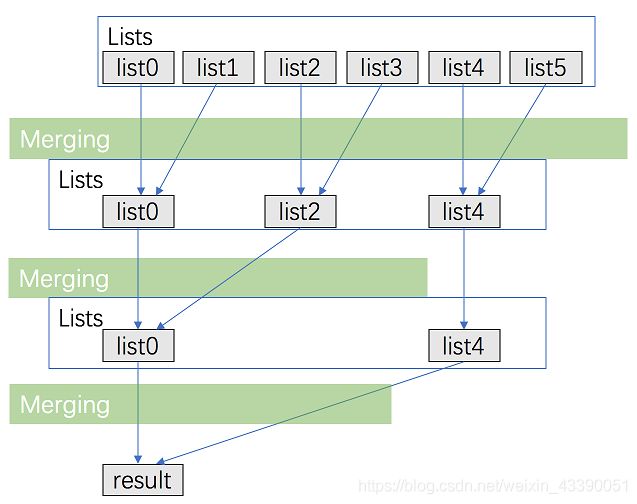
$result=merge(lists,0,n-1)=merge2list(merge(lists,0,\frac{n-1}{2}),merge(lists,\frac{n+1}{2},n-1))$表示合并一个升序链表向量，等于将其分成两半，分别将各一半的链表进行合并后，再将这两个合并好之后的链表进行合并。
递归的边界条件为:
$merge(lists,i,j)，if(i==j)returnlists[i]$

思路二：优先级队列

假设有k个升序链表，建立一个长度为k的优先级队列，来存放每个链表的头部结点，由于优先队列的队首是最小值（需重载运算符），故每次只需取队首结点插入到结果链表中，然后队首节点所在的链表移到下一个结点。

trick:优先级队列（priority_queue+重载运算符）

struct Node
    {
        ListNode* node;
        bool operator < (const Node &a) const
        {
            return node->val > a.node->val;
        }
    };
priority_queue<Node>q;

双向链表+哈希表

双向链表+哈希表可以让删除增添操作的复杂度为O(1).
哈希表定位双向链表中结点位置，通过节点pre,next指针可以快速将其删除或者添加。

哈希函数

705.设计哈希集合

trick：bitset

bitset可用于直接表示哈希函数，由于其每一个位置只占1位，因此所占的空间很小，且查找的时间非常快。

bitset<1000001>hash;
void add(int key) {
	hash[key]=true;
    }
    
void remove(int key) {
    hash[key]=false;
    }

49.字母异位词分组

由于字母异位词，字母数量相同，因此可以将字符串进行排序后，作为哈希表的键值。

560.和为K的子数组

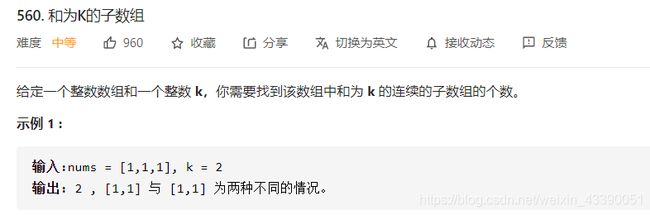
依次遍历数组，在遍历的同时，计算前缀和，并使用hash表来记录前缀和的数量。当遍历到数组中的某个元素时，假设位置为$i$，元素为$nums[i]$，则判断哈希表中存储的前缀和为$sum[i]-k$的数量，即可得到$i$前面的元素中连续子数组和为$k$的个数。

树

广度优先遍历（层次遍历）

可使用一个队列来存储遍历到的结点，即可实现广度优先遍历。

根据前序遍历和中序遍历构造二叉树

前序遍历顺序为头->左->右，而中序遍历为左->中->右，因此可以根据前序遍历序列中，找到头结点，从而对应到中序遍历中，递归构建二叉树。

多叉树

定义：

struct Node
{
    Node *next[NUM]; 
};

每一个结点都有多个子节点，在分配next结点时，需要对next进行初始化0操作

memset函数

初始化数组，将数组均设为初值0(NULL)。

前缀树题208

#include
memset(Node->next,0,sizeof(Node->next));

字符串

179.最大数

定义比较函数：

sort(int2str.begin(), int2str.end(), [](string& a, string& b)
{return a + b > b + a;}
);

字符串之间的比较是从左往右依次比
同时to_string()函数可以将整数型转换为字符型。

Boyer-Moore投票法求众数

设置一个candidate作为众数，count为计数，依次遍历每一个元素，当count=0时则更换candidate：

for(int i=0;i<n;++i)
{
    if(!count)
    {
        candidate=nums[i];
        count++;
    }
    else if(candidate==nums[i])count++;
    else count--;
}

摩尔投票法的思路可以如下：

优先队列priority_queue

692.前k个高频单词

1. 哈希+排序

哈希表map中不能直接对value进行排序，只能将hash表转换到vector中，再在vector中自定义排序。

2. 优先队列priority_queue

遇到这种求前k个，可用优先级队列。优先级队列可以自定义排序方式：
定义排序方式：注意，return a
优先级队列定义方式：

239.滑动窗口求最大值

思路一.优先级队列（大顶堆）

依次遍历数组，当遍历到位置大于k-1时，则将当前的元素及其下标加入到优先级队列中，并依次判断堆顶元素的下标是否还在范围内，若不在，则依次取掉堆顶元素，最终堆顶元素即为最大值。

思路二.双向队列deque 实现单调队列

对于前k-1个元素，维护一个从队首到队尾单调递减的队列，队列存储的是对应的下标值。当遍历到位置大于k-1时，先将该元素添加至该单调队列中，再从队首判断队首元素的下标是否处在范围之内，否则则去除掉队首元素。
由于涉及到同时需要在队首以及队尾消除元素，因此采用双向队列。

子数组

532.连续子数组和（同余定理）

若m-n%k=0，则m%k=n%k

双向广度优先

从初始状态和target状态两个方向进行广度优先遍历。

A*启发式算法

在广度优先的基础上，每次挑选总距离最短的，进行下一次遍历：
$f(n)=g(n)+h(n)$，其中$f(n)$表示起点到当前点走过的距离，$h(n)$表示当前点到终点的估计距离，这个距离可以为曼哈顿距离或者欧氏距离，每次挑选队列中$f(n)$最小的进行遍历。

图

207.课程表

广度优先搜索

利用哈希表来存储每个结点的后继结点，然后单独开放一个数组来存储每个结点的入度数。将入度数为0的结点放入队列中，然后从队列中每取出一个结点，就将其定位到哈希表中，将其后继结点的入度数-1，并且当后继结点入度数为0时，则添加进队列中。
当队列为空时，且遍历入度表，若发现还有节点的入度数不为0，则说明存在环，若没有则不存在。

深度优先搜索

还是利用哈希表才存储后继结点，依次对第0…numCourses-1课进行深度优先遍历。对每个结点设置三种状态：
1：当前结点进行DFS
0：未进行DFS
-1：其他结点发起的DFS
若DFS遍历到某个节点，其状态为1，则直接返回False；若为-1，则说明已被其他DFS过，直接返回True；若为0，则继续进行dfs。
具体动画见：
https://leetcode-cn.com/problems/course-schedule/solution/course-schedule-tuo-bu-pai-xu-bfsdfsliang-chong-fa/
深度优先部分代码如下

bool dfs(unordered_map<int,vector<int>>&hash,vector<int>&flags,int i)
{
    if(flags[i]==1)return false;
    if(flags[i]==-1)return true;
    flags[i]=1;
    if(hash.find(i)!=hash.end())
    {
        for(int k:hash[i])
        {
            if(!dfs(hash,flags,k))
                return false;
        }
    }
    flags[i]=-1;
    return true;
}

Tricks

1.string_to_integer

int i;
string s;
i=atoi(s.c_str());

2.integer_to_string

to_string()

3.函数形参传入引用，速度会更快

4.异或

a⊕b⊕a=b 因此可将所有数字进行异或，最终可以得到只出现了一次的数字。

5.计算二进制1的数目__builtin_popcount()

6.合理使用bitset或者位运算，可节省大量时间

1239.串联字符串的最大长度

使用26位运算（或者bitset）以及深度优先来解题。

function<void(int, bitset<26>)> dfs = [&](int pos, bitset<26> mask)
{
    if(pos==masks.size())
    {
        res=max(res,int(mask.count()));
        return;
    }
    //如果当前字符串masks[pos]与之前的字符串mask无重复字符(mask&masks[pos]==0)
    //则可选择 选择加入该字符串或者不加入该字符串
    if((mask&masks[pos])==0)
        dfs(pos+1,mask|masks[pos]);
    dfs(pos+1,mask);
};