Leetcode每日一题（困难）：834. 树中距离之和（2023.7.16 C++）

目录

834. 树中距离之和

题目描述：

实现代码与解析：

DFS

原理思路：

---

834. 树中距离之和

题目描述：

        给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例 1:

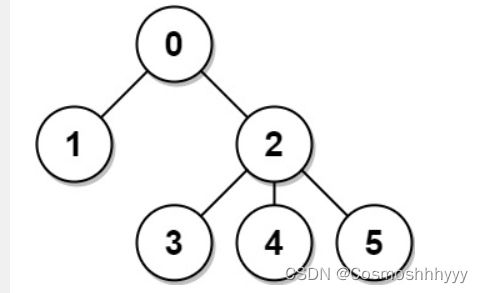
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

示例 2:

输入: n = 1, edges = []
输出: [0]

示例 3:

输入: n = 2, edges = [[1,0]]
输出: [1,1]

实现代码与解析：

DFS

class Solution {
public:
    int nodeNum[300010]; // 结点 i 所在子树的结点个数
    int distSum[300010]; // 第一次dfs：结点 i 所在的子树的结点到 i 距离和。
                        // 第二次dfs2：结果，结点 i 到所有节点的距离和。
    int h[300010], e[300010], ne[300010], idx; // 邻接表

    // 邻接表加边
    void add(int a, int b)
    {
        e[idx] = b, ne[idx] = h[a], h[a] = idx++;
    }

    // 后序遍历
    void dfs(int u, int f)
    {
        for (int i = h[u]; ~i; i = ne[i])
        {
            int j = e[i];
            if (j == f) continue; // 防止遍历回去
            dfs(j, u); // 开始继续计算

            nodeNum[u] += nodeNum[j]; // nodeNum 初始化就为1，不用再单独＋1了
            distSum[u] += distSum[j] + nodeNum[j]; // 等于子树距离和 + 此边要走的此数（也就是子树结点数）
        }
    }

    // 先序遍历
    void dfs2(int u, int f, int n)
    {
        for (int i = h[u]; ~i; i = ne[i])
        {
            int j = e[i];
            if (j == f) continue;
            distSum[j] = distSum[u] - nodeNum[j] + (n - nodeNum[j]); // 这里用到总的节点个数了，参数加上n
            dfs2(j, u, n);
        }
    }
    vector sumOfDistancesInTree(int n, vector>& edges) {

        // 初始化
        memset(h, -1, sizeof h);
        memset(distSum, 0, sizeof distSum);
        for (int i = 0; i < n; i++) nodeNum[i] = 1;

        // 构建邻接表边
        for (int i = 0; i < edges.size(); i++)
        {
            add(edges[i][0], edges[i][1]);
            add(edges[i][1], edges[i][0]);
        }

        dfs(0, -1);
        dfs2(0, -1, n);
        // 截取结果
        vector res;
        res.assign(distSum, distSum + n);
        return res;
    }
};

原理思路：

        首先，我们要算出每个以 i 为根结点的子树的结点数量 nodeNum[i] 和 i 到子树其他结点的距离总和distSum[i]。

        结点数量很好计算，但是 distSum[i] 如何计算呢？用例 1 举例，当计算2的distSum时：

可以发现，其不单单是子树的 dist 相加，还要加上其各自的结点数量，因为其子树的各个结点想要到达根节点都需要经过一次此边。

nodeNum[u] += nodeNum[j]; // nodeNum 初始化就为1，不用再单独＋1了
distSum[u] += distSum[j] + nodeNum[j]; // 等于子树距离和 + 此边要走的此数（也就是子树结点数）

        我们会发现现在 distSum 的含义是表示根结点 i 到其子树结点的距离和，并不是我们的结果。

        那么结果（也就是节点 i 到树中每一个结点的距离总和）如何计算呢？还是拿例 1 举例，根据现在 distSum 的含义 distSum[0]（也就是根节点）就是我们的一个结果，我们可以利用此结果自顶向下的遍历，找出子树结果和根结果的关系，推算出每个节点的最终distSum(真正的结果)。

        这样就有此题最关键的核心问题？如何根据根结点的结果计算出子树根结点的结果呢？

        就例 1 来说，我们还是算节结 2 的时候（这时候是第二次遍历，自顶向下），我们用已经算出结果的distSum[0] - nodeNum[2]，结点 0 到各个结点的距离总和 减去 以结点2为根节点的子树结点个数，这样减去得到的数字含义为：结点 0 到 结点1 的距离（普遍来说是到其他子树的结点距离总和） 加上 结点 2 到以结点 2 为根的子树的结点距离总和。可见还不是我们要的结果，我们再把数字加上除结点2这颗子树的节点个数（此例中就为2个，也就是结点 0 和 1），为什么要加呢？还是一样的道理，结点 0 和 1 想要到达结点 2 都需要走结点0 - 2这条边两次。

distSum[j] = distSum[u] - nodeNum[j] + (n - nodeNum[j]); // 这里用到总的节点个数了，参数加上n

        这样我们就能算出结果了。至于邻接表如何建立和如何遍历是属于基础，每个人写法可能不太一样（当然原理都是一样的），这里就不再详细解释了，不会的可以去查一查。