【数据结构】七大排序算法（超详细）

  欢迎来到南方有乔木的博客！！！

---

博主主页：点击点击！戳一戳！！

博主名:南方有乔木

博主简介：

一名在校大学生，正在努力学习Java语言编程。穷且意坚，不坠青云之志，希望能在编程的世界里找到属于自己的光。

跪谢帅气or美丽的朋友们能够帮我点赞! 请对文中内容请多多指教！！！

​

目录

一.排序算法简介

1.内部排序

2.外部排序

二.排序算法的分类

三.七大排序算法的实现

1.冒泡排序（交换排序之一）

 2.快速排序（交换排序之一）

 3.直接选择排序（选择排序之一）

4.堆排序（选择排序之一）

5.直接插入排序（插入排序之一）

6.希尔排序（插入排序之一）

7.归并排序

---

一.排序算法简介

排序的定义：

排序就是将一组无序的数据排序成有序的序列的操作。

排序分类：

1.内部排序

内部排序是指待排序序列全部存放在内存中的进行的排序过程。这种方法适用于数量不大的数据元素的排序。

2.外部排序

外部排序是指需要排序的数据非常的多，它们必须存储在外部的存储器上，这种排序的过程需要访问外部存储器，这种排序就是外部排序。

排序的稳定性

概念：

对于一组数据元素序列，使用某种排序算法对它进行排序，若相同数据之间的前后位置排序后和未排序之前是相同的，我们就称这种排序算法是具有稳定性的。

比如 关键字序列：

1，5a，3，7，5b，9，12

这个序列中有两个5，我们将第一个数字记成5a，第二个5记为5b,若排序后：

1，3，5a，5b，7，9，12

5a还是在5b之前，相对位置不变，称排序所用的算法具有稳定性

若排序后：

1，3，5b，5a，7，9，12

5b变到了5a之前，相对位置发生变化，则称排序的算法不具有稳定性。

二.排序算法的分类

常见的七大基于比较的排序算法一共有七种，分别是，冒泡排序

直接选择排序，希尔排序，快速排序，堆排序，直接插入排序，归并排序。

分类示意图：

根据它们的特性这七种算法又被分成了四类

1.选择排序：直接选择排序，堆排序

2.插入排序：直接插入排序，希尔排序

3.交换排序：冒泡排序，快速排序

4.归并排序：归并排序

三.七大排序算法的实现

1.冒泡排序（交换排序之一）

示意图：

原理：

在无序区间中，将两两相邻的元素进行比较，每一轮比较出最大的一个元素，交换到有序区间。

步骤：

1.冒泡排序的主要思想是两两比较，因此先确定要比较多少次，因为前面经过比较只剩最后一个元素的时候，最后一个元素必定已经有序，因此，如果有n个元素，只需要比较n-1次。

2.进行两两比较的过程，从第一个元素开始，把它与它两两相邻的元素比较，把大的换到右边，一直比较，直到把数组里最大的元素换到最右边，因为只需要比较到倒数第二个元素的时候，它与倒数第一个元素比较已经可以换到最右边，因此下标只需要到数组的倒数第二个就行。

实现：

import java.util.Arrays;
public class BubbleSort {
   //实现数组内两元素交换
    public static void swap(int[]array,int i,int j){
        int temp=array[i];
        array[i]=array[j];
        array[j]=temp;
    }
    //冒泡排序
    public static void bubbleSort(int[]array){
        int size=array.length;
      //一开始控制进行两两比较的次数，最后一轮必定有序，所有比较次数为size-1次
        for(int i=0;iarray[j+1]){
                    swap(array,j,j+1);
                    //若发生交换则说明已经还未有序
                    sort=false;
                }
            }
            if(sort==true){
                //一轮比较后未发生交换，说明已经有序
                return ;
            }
        }
    }
    public static void main(String[] args) {
        int[]arr={1,3,5,0,8,2,6};
        bubbleSort(arr);
        System.out.println("冒泡排序："+Arrays.toString(arr));
    }
}

 执行结果：

 2.快速排序（交换排序之一）

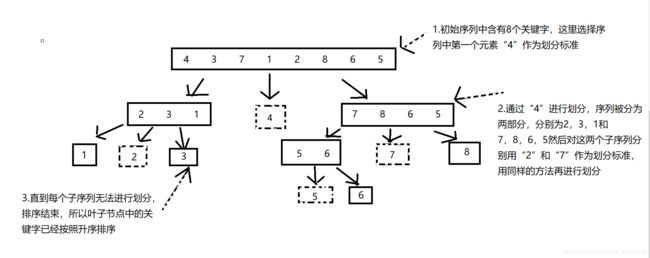
示意图：

原理：

从待排序的区间取一个基准值，比基准值大的放到基准值的右边，比基准值小的放到基准值的左边，对于左右两边，再次充分这样的步骤。

快速排序是冒泡排序的改进算法，它采用了分治的思想，将原问题划分为若干个规模更小的子问题，子问题的依旧与原问题是相似的，递归解决所有的子问题，也就解决了原问题。

步骤：

1.从待排序区间取一个数作为基准值

2.遍历待排序区间，把所有比基准值小的数放到基准值的左边，比基准值大的放到基准值的右边，这个过程使用专业的术语叫做parttion.

3.对于基准值的左右两边重复以上过程，直到整个序列变得有序。

实现：

import java.util.Arrays;
public class QuickSort {
    public static void swap(int[]arr,int i,int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    private static void quickSort(int[]arr){
        quickSortRange(arr,0,arr.length-1);

    }
    private static void quickSortRange(int[]arr,int formIndex,int toIndex){
        //求出要求数组区间的元素个数
        int size=toIndex-formIndex+1;
        if(size<=1){
            return;
        }
        int pivotIdx=partition(arr,formIndex,toIndex);
        quickSortRange(arr,formIndex,pivotIdx-1);
        quickSortRange(arr,pivotIdx+1,toIndex);
    }
    //partition Hoare法
    private static int partition(int[]arr,int formIndex,int toIndex){

        int lefIdx=formIndex;
        int rigIdx=toIndex;

        int pivot=arr[toIndex];

        while(rigIdx>lefIdx){
            while(rigIdx>lefIdx&&arr[lefIdx]<=pivot){
                lefIdx++;
            }
            //此循环结束说明找到了大于基准值的元素
            while(rigIdx>lefIdx&&arr[rigIdx]>=pivot){
                rigIdx--;
            }
            //此循环结束说明找到了小于基准值的元素
            swap(arr,lefIdx,rigIdx);

        }
        swap(arr,lefIdx,toIndex);
        return lefIdx;
    }


  //检测：
    public static void main(String[] args) {
        int[]arr={1,5,2,4,8,3,7,10};
        quickSort(arr);
        System.out.println(Arrays.toString(arr));

    }
}

运行结果：

 3.直接选择排序（选择排序之一）

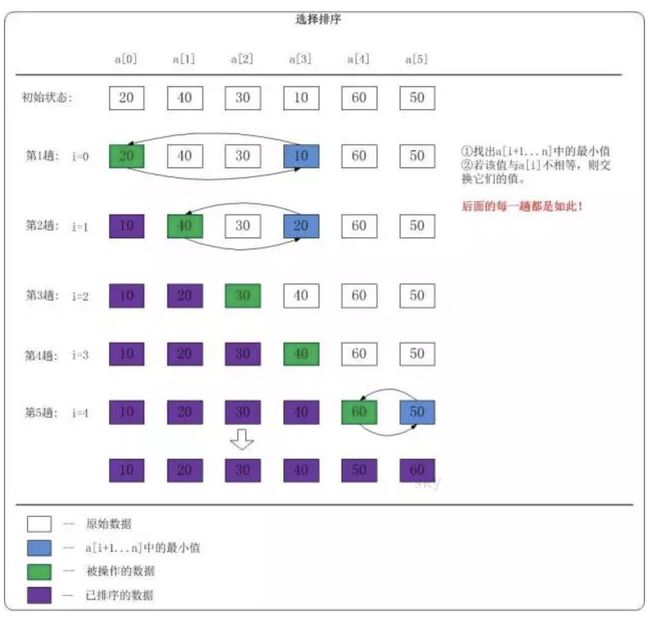
示意图：

原理：

每一次从无序区间选出最大（或者最小）的元素，放在有序区间的最后（或者无序区间的最前），直到所有的元素有序。

步骤：（此步骤针对无序区间在前，有序区间在后）

1.找到到无序区间的最大值元素的下标

2.将无序区间最大值元素的下标交换到有序区间的最后一个

3.重复此过程，直到数组有序

实现：

import java.util.Arrays;
public class SelectSort {
    private static void swap(int[]arr,int i,int j){

        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
    }
   //直接选择排序（无序区间在前，有序区间在后的写法）
    public static void selectSort(int[]arr,int size) {
        //外层需要选择size-1次
        for (int i = 0; i < size - 1; i++) {
            //无序区间 [0,size-i)

            //有序区间 [size-i,size)
            //要找到一个最大值下标，可以先假设最大值下标，再拿其他与它比较
            int maxIdx = 0;
            //遍历整个无序区间
            int j=0;//已经取了第一个元素为最大
            //遍历时从第二个元素开始遍历
            for( j=1;jarr[j]){
                    minIdx=j;
                }
            }
            //找到无序区间的最小值以后，交换到无序区间的第一个元素
            swap(arr,minIdx,i);
        }

    }
    //直接选择排序（左边为有序区间，中间为无序区间，右边为无序区间）
    //每次找出最大与最小，最大往右边有序区间移，最小往左边有序区间移

    public static void selectSort3(int[]arr,int size){


    }
//简单测试：
    public static void main(String[] args) {
        int[]arr={9,8,5,9,2,3,4};
        selectSort2(arr, arr.length);
        System.out.println(Arrays.toString(arr));
    }

}

简单测试结果：

4.堆排序（选择排序之一）

示意图：

原理：

堆排序也是选择排序中的一种，找到无序区间中的最大值（或者最小值），将它交换到有序区间的最后（或者无序区间的最前）。与直接选择排序最大的不同在于，它不在使用遍历的方式来寻找无序区间的最大值（或最小值），而是通过创建堆的方式来创建最大值（或者最小值）。

步骤：

1.创建堆，要创建堆，先实现向下调整。

2.创建堆以后，堆顶元素就是最大值，找到了最大值就将它交换到最后，放到无序区间的最后

3.放到无序区间最后以后，再从堆顶进行向下调整，调整长度减掉有序区间的长度

实现：

import java.util.Arrays;
public class HeapSort{

    // 堆排序
       public static void heapSort(int[] array){
        createHeap(array);
        for(int i=0;i=0;i--){
            //创建最大堆
            shiftDown2(array,array.length,i);
        }
        }

     //最大堆向下调整
        public static void shiftDown2(int[]array,int size,int index){

        while(true){
          int leftIdx=2*index+1;
          if(leftIdx>=size){
              return;
          }
          int maxIdx=leftIdx;
          if(leftIdx+1array[leftIdx]){
              maxIdx=leftIdx+1;
          }
          if(array[maxIdx]<=array[index]){
              return ;
          }
          swap(array,maxIdx,index);
          index=maxIdx;
       }
      }

        public static void main (String[]args){
           //简单测试

            int[] arr2 = {27, 15, 19, 18, 28, 34, 65, 49, 25, 37};
            shiftDown(arr2, 0,arr2.length);
            System.out.println("向下调整："+Arrays.toString(arr2));

            int[]arr3={8,4,6,5,1,3};
            createHeap(arr3);
            System.out.println("创建堆："+Arrays.toString(arr3));

            int[]arr4={1,0,9,55,4,5,8,3};
            heapSort(arr4);
            System.out.println("堆排序"+Arrays.toString(arr4));

        }
}

简单测试结果:

5.直接插入排序（插入排序之一）

示意图

原理：

每次在无序区间选择无序区间的第一个元素，在有序区间找到合理的位置插入。可以将它想象成平时打牌我们对于扑克牌的排序。

步骤：

1.遍历整个无序区间，循环选择无序区间的第一个元素

2.在有序区间找到合适的位置，进行插入即可。（在插入时，要提前把不合适的位置往后搬）

实现：

import java.util.Arrays;

//插入排序
public class InsertSort {

    //对数组全部做插入排序
    public static void insertSort(int[]arr,int size){
        //一开始认为第一个数已经有序
        for(int i=1;i=0&&key=arr[j]找到了合适的插入位置
            //找到key>=arr[j]后，插入到arr[j]的后面就是arr[j+1]位置
            arr[j+1]=key;
        }
    }
    //对指定范围做插入排序
    public static void insertSort2(int[]arr,int formIndex,int toIndex){
        int n=toIndex-formIndex;
        for(int i=1;i=formIndex&&key

简单测试结果：

6.希尔排序（插入排序之一）

原理：

希尔排序还叫做缩小增量排序。它开始先选定一个增量gap，把间隔为增量gap的数分为一组，对每个组内进行插入排序。一次排序完成后，缩小增量，再次分组，再次对每个组内进行插入排序。当增量gap==1，说明数组已经有序。

步骤：

1.确定增量，根据增量进行分组。

2.对每组内元素进行插入排序。

3.完成上两步后缩小增量，再次循环进行

4.当增量==1，数组有序，排序结束

import java.util.Arrays;

public class ShellSort {
    //希尔排序

    private static void shellSort(int[]arr){
        //假设有10个元素就分5组
        int group= arr.length/2;
        //分组后循环对每个组内的元素进行插入排序
        while(true){
            insertSortWithGroup(arr,group);
            if(group==1){
                //如果只剩一组说明已经有序
                return;
            }
            //每次排序后再分组
            group=group/2;
        }
    }

    //希尔排序分组后对每一组的插入排序方法
    private static void insertSortWithGroup(int[]arr,int group){

        for(int i=group;i< arr.length;i++){
            int key=arr[i];
            int j=i-group;
            for( j=i-group;j>=0&&key

简单测试结果：

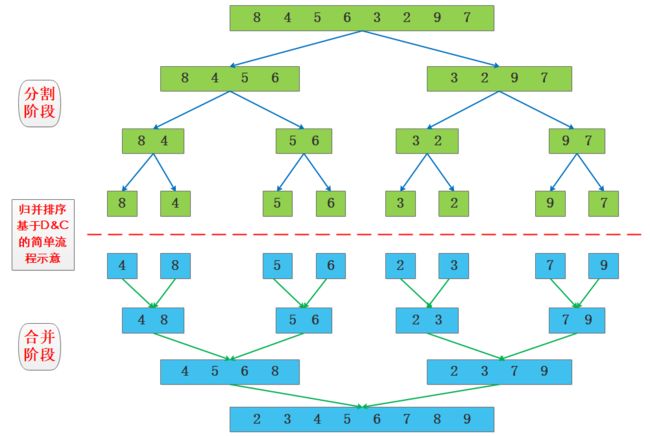
7.归并排序

示意图：

原理：

归并排序的原理是原序列先分割成一个一个的小的子序列，先使每个子序列有序，再将子序列合并，得到一个完整的有序序列，这就是归并排序。

（我这里采用二路归并）步骤：

1.先将原来的无序序列分割成若干个子序列，当分割到一个序列里只有一个元素时说明分割完毕。

2.再将分割后的子序列不断归并，归并的原理是合并两个有序的子序列，一直归并，直到归并得到一个完整的序列。

实现：

import java.util.Arrays;
public class MergeSort {
    public static void mergeSort(int[] array){
        mergeSortFunc1(array,0,array.length-1);
    }
    public static void mergeSortFunc1(int[]array,int left,int right){
        //开始先分割
        if(left>=right){
            return ;
        }
        int mid=(left+right)/2;
        //递归左区间和递归右区间分割
        mergeSortFunc1(array,left,mid);
        mergeSortFunc1(array,mid+1,right);
        //分割后合并
        merge(array,left,mid,right);

    }
     // 合并原理：合并两个有序数组
    public static void merge(int[]array,int start,int mid,int end){

        //先分别找出两个数组中第一个更小的元素，将更小的元素搬到
        //额外空间
        int[] extra=new int[end-start+1];

        int i=start;
        int j=mid+1;
        int k=0;
        //两个数组都还有元素时
        while(i<=mid&&j<=end){
            if(array[i]<=array[j]){
                 extra[k++]=array[i++];
            }else {
                extra[k++] = array[j++];
            }
        }
        //当有一个数组已经搬完时，需要判断哪个数组搬完了
        while(i<=mid){
            //把没有搬完的数组全部搬到额外数组
            extra[k++]=array[i++];
        }
        while(j<=end){
            //把没有搬完的数组全部搬到额外数组
          extra[k++]=array[j++];
        }
        //全部搬到额外空间时，再搬回原数组

        for(int n=0;n

 简单测试结果：

以上就是7种常见的排序算法，对于排序算法，必须需要掌握它们的基本原理，只有知道了它们的基本原理，我们才能够根据原理写出对应的实现代码。