【算法和数据结构】347、LeetCode前 K 个高频元素

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

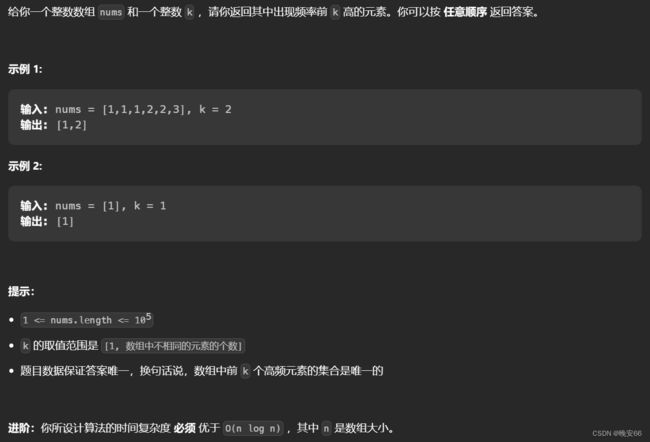
一、题目

二、解法

  思路分析：首先我们使用一个哈希表记录每个元素出现的频率。再设置一个优先队列，并将数组中元素出现的频率和该元素依次加入到优先队列。由于优先队列会自动进行排序，所以此时优先队列中存储的值就是按照频率进行排序的。注意排序是按照对组的第一个元素进行，插入优先队列后，对组的first代表元素频率，对组的second代表插入的元素。最后设置一个结果数组，再根据题目中的要求向数组中压入需要的k个最大频率的元素即可。
  程序如下：

	vector<int> topKFrequent(vector<int>& nums, int k) {
		unordered_map<int, int> m;
		for (int num : nums) m[num]++;	// 记录元素出现频率，num代表元素，value代表出现的频率
		priority_queue<pair<int, int>> que;			
		for (auto i : m) que.emplace(i.second, i.first);	// 降序排列，大根堆，频次最高的元素在队头
		vector<int> result(k);
		while (!que.empty() && k--) {
			result.emplace_back(que.top().second);
			que.pop();
		}
		return result;
	}

复杂度分析：

• 时间复杂度： $O(n\ast logn)$。记录元素出现频率需要的复杂度为$O(n)$，然后遍历频率数组复杂度为$O(n)$，其中优先级队列又要插入频率数组，大顶堆的插入操作复杂度为$O(logn)$，最后向结果数组插入k个最大元素,复杂度为$O(k)$。总复杂度为$O(n+n\ast logn+k)=O(n\ast logn)$。
• 空间复杂度：$O(n)$。

  代码优化：这道题的时间复杂度还可以进一步优化。我们首先要意识到目标是最大的K个频率的元素，因此没有必要将所有的元素都插进优先队列当中，仅仅需要插入K个最大出现频率的元素即可。那么需要与已经插入的K个元素进行对比，此时大根堆就不在适用了，找到最小的值就很困难。因此我们使用小根堆，如果插入元素大于堆顶（小根堆，最小元素），那么插入元素，同时弹出堆顶。使用这种方式只需要维护K个元素的优先级队列，插入的次数也仅仅为$O(logk)$，因此总时间复杂度为$O(n\ast logk)$。
  程序如下：

	vector<int> topKFrequent2(vector<int>& nums, int k) {
		class mycomparison {	// 为小顶堆提供比较函数
		public:
			bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
				return lhs.second > rhs.second;
			}
		};
		unordered_map<int, int> m;
		for (int num : nums) m[num]++;	// 记录元素出现频率，key/num代表元素，value代表出现的频率
		priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> que;
		for (unordered_map<int, int>::iterator it = m.begin(); it != m.end(); it++) {
			que.push(*it);
			if (que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
				que.pop();
			}
		}
		vector<int> result(k);		// 向结果数组中插入K个最大元素
		for (int i = k - 1; i >= 0; i--) {
			result[i] = que.top().first;
			que.pop();
		}
		return result;
	}

三、完整代码

# include 
# include 
# include 
# include 
using namespace std;

class Solution {
public:
	vector<int> topKFrequent(vector<int>& nums, int k) {
		unordered_map<int, int> m;
		for (int num : nums) m[num]++;	// 记录元素出现频率，num代表元素，value代表出现的频率
		priority_queue<pair<int, int>> que;			
		for (auto i : m) que.emplace(i.second, i.first);	// 降序排列，大根堆，频次最高的元素在队头
		vector<int> result(k);
		while (!que.empty() && k--) {
			result.emplace_back(que.top().second);
			que.pop();
		}
		return result;
	}

	vector<int> topKFrequent2(vector<int>& nums, int k) {
		class mycomparison {	// 为小顶堆提供比较函数
		public:
			bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
				return lhs.second > rhs.second;
			}
		};
		unordered_map<int, int> m;
		for (int num : nums) m[num]++;	// 记录元素出现频率，key/num代表元素，value代表出现的频率
		priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> que;
		for (unordered_map<int, int>::iterator it = m.begin(); it != m.end(); it++) {
			que.push(*it);
			if (que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为k
				que.pop();
			}
		}
		vector<int> result(k);		// 向结果数组中插入K个最大元素
		for (int i = k - 1; i >= 0; i--) {
			result[i] = que.top().first;
			que.pop();
		}
		return result;
	}
};

void my_print(vector <int>& v, string msg)
{
	cout << msg << endl;
	for (vector<int>::iterator it = v.begin(); it != v.end(); it++) {
		cout << *it << "  ";
	}
	cout << endl;
}

void VectorGenerator(int* arr, vector<int>& v, int arr_len) {
	for (int i = 0; i < arr_len; ++i) {
		v.push_back(arr[i]);
	}
}

int main(){
	int topK = 2;
	int arr[] = { 1,1,1,2,2,3 };
	int arr_len = sizeof(arr) / sizeof(int);
	vector<int> nums;
	VectorGenerator(arr, nums, arr_len);
	my_print(nums, "目标数组");
	Solution s1;
	vector<int> result = s1.topKFrequent2(nums, topK);
	my_print(result, "频率最高的元素");
	system("pause");
	return 0;
}

end