轻松入门Python量化交易(二)
大家好,我们继续接上文分析金融数据。
直方图
直方图是数据集中值的分布图形表示,显示这些值的频率。
每日收益率的直方图有助于帮助投资者识别模式,例如某个资产在一定期间内的每日收益率范围,表明其稳定性和波动性水平,再次使用Quantstats绘制所分析资产的直方图。
# 绘制直方图
print('\nApple Daily Returns Histogram')
qs.plots.histogram(aapl, resample = 'D')
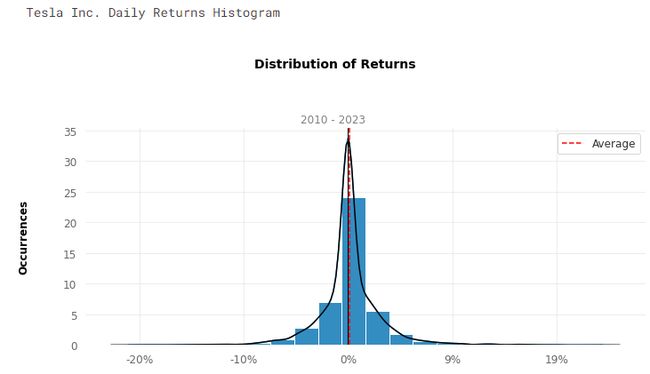
print('\nTesla Inc. Daily Returns Histogram')
qs.plots.histogram(tsla, resample = 'D')
print('\nThe Walt Disney Company Daily Returns Histogram')
qs.plots.histogram(dis, resample = 'D')
print('\nAdvances Micro Devices, Inc. Daily Returns Histogram')
qs.plots.histogram(amd, resample = 'D')
通过对直方图的分析,我们可以观察到大多数每日收益率在分布的中心接近于零。但是,很容易看到一些远离均值的极端值,这就是AMD的情况,每的日收益率约为50%,表明在分布的正值范围存在离群值。相反,在负值范围内,似乎有一个约为-20%的限制。迪士尼似乎显示出更平衡的收益率,其价值范围在-15%到15%之间,而大部分收益率更接近于平均值。
使用直方图,我们可以提取一些有价值的统计数据,例如峰度和偏度。
峰度
每日收益率的高峰度值可能表明价格的频繁波动明显偏离该投资的平均收益率,这可能导致波动性和风险增加。峰度值超过3.0的分布称为尖峰分布,其特征是离群值和更多远离平均值的值,这会在直方图中表现为水平轴的拉伸。具有尖峰分布的证券通常与更高的风险水平相关,但也因为过去发生的大幅价格变动而具有更高的回报潜力。
在下面的图像中,可以看到左边是负峰度,右边是正峰度。左边的分布显示极端值的概率较低,平均值附近的数值集中度也较低,而右边的分布显示平均值附近的数值集中度较高,但也存在极端值,因此发生的概率也较高。
在金融领域,高水平的过度峰度,或“尾部风险”,代表了因罕见事件而发生损失的可能性。这种风险对于投资者在做出投资决策时考虑是非常重要的,因为它可能会影响特定证券的潜在回报和稳定性。
同样,我们使用quantstats来测量所分析峰度。
# 使用quantstats来测量峰度
print("Apple's kurtosis: ", qs.stats.kurtosis(aapl).round(2))
print("Tesla's kurtosis: ", qs.stats.kurtosis(tsla).round(2))
print("Walt Disney's kurtosis: ", qs.stats.kurtosis(dis).round(3))
print("Advances Micro Devices' kurtosis: ", qs.stats.kurtosis(amd).round(3))Apple's kurtosis: 5.26
Tesla's kurtosis: 5.04
Walt Disney's kurtosis: 11.033
Advances Micro Devices' kurtosis: 17.125上述峰度值显示,苹果、特斯拉等这些证券都具有很高的峰度水平,这表明它们的每日收益分布观测值集中在尾部,表明这些证券面临很高的波动率和风险,价格波动明显偏离平均收益。
偏度
偏度是量化收益不对称性的指标。它反映了分布的形状,并确定它是否对称、左偏或右偏。使用quantstats和Python可以计算偏度,如下所示:
# 使用quantstats测量偏度
print("Apple's skewness: ", qs.stats.skew(aapl).round(2))
print("Tesla's skewness: ", qs.stats.skew(tsla).round(2))
print("Walt Disney's skewness: ", qs.stats.skew(dis).round(3))
print("Advances Micro Devices' skewness: ", qs.stats.skew(amd).round(3))Apple's skewness: -0.07
Tesla's skewness: 0.33
Walt Disney's skewness: 0.199
Advances Micro Devices' skewness: 1.043通常,-0.5到0.5之间的值表示轻微的偏斜,而小于-1和大于1的值则表示强烈的不对称。
标准差
标准差是广泛使用的统计指标,用于量化数据集的变异性。当应用于证券的每日收益时,它可以指示与投资特定证券相关的风险水平,具有高的每日收益波动性(高标准差)的证券被认为比每日收益波动性较低(低标准差)的更具风险。
标准差使投资者能够评估风险水平,比较不同证券的波动性。例如,如果两个资产具有相似的平均回报,但一个的标准差更高,通常被认为是更具风险的投资。因此,标准差是帮助投资者在投资选择和投资组合管理方面做出明智决策的有用工具。
# 使用quantstats测量标准差
print("Apple's Standard Deviation from 2010 to 2023: ", aapl.std().round(3))
print("\nTesla's Standard Deviation from 2010 to 2023: ", tsla.std().round(3))
print("\nDisney's Standard Deviation from 2010 to 2023: ", dis.std().round(3))
print("\nAMD's Standard Deviation from 2010 to 2023: ", amd.std().round(3))Apple's Standard Deviation from 2010 to 2023: 0.018
Tesla's Standard Deviation from 2010 to 2023: 0.036
Disney's Standard Deviation from 2010 to 2023: 0.016
AMD's Standard Deviation from 2010 to 2023: 0.036根据上述数值,我们可以说,苹果和迪士尼的波动性比特斯拉和AMD小,这表明苹果和迪士尼是更安全的投资选择,在市场上表现出更小的价格波动。