【复习10-12天内容】【我们一起60天准备考研算法面试(大全)-第十四天 14/60】
专注 效率 记忆
预习 笔记 复习 做题
欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录)
文章字体风格:
红色文字表示:重难点★✔
蓝色文字表示:思路以及想法★✔
如果大家觉得有帮助的话,感谢大家帮忙
点赞!收藏!转发!
本博客带大家一起学习,我们不图快,只求稳扎稳打。
由于我高三是在家自学的,经验教训告诉我,学习一定要长期积累,并且复习,所以我推出此系列。
只求每天坚持40分钟,一周学5天,复习2天
也就是一周学10道题
60天后我们就可以学完81道题,相信60天后,我们一定可以有扎实的代码基础!我们每天就40分钟,和我一起坚持下去吧!
qq群:878080619
第十四天【考研408-数据结构(笔试)】
- 十一、KMP
- 十二、排序
-
- 1. 快速排序
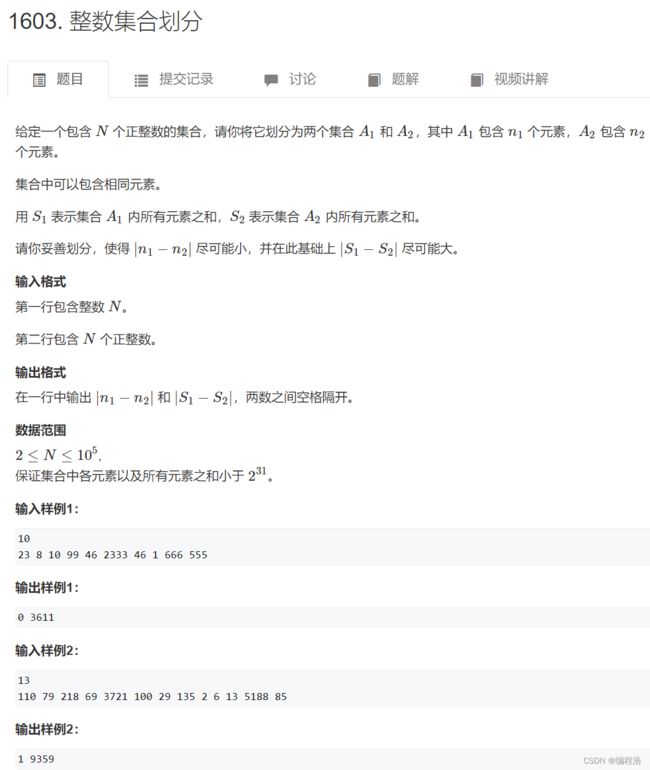
- 2. 整数集合划分
- 十三、多路归并
-
- 1. 三元组的最小距离(2020年全国硕士研究生招生考试)
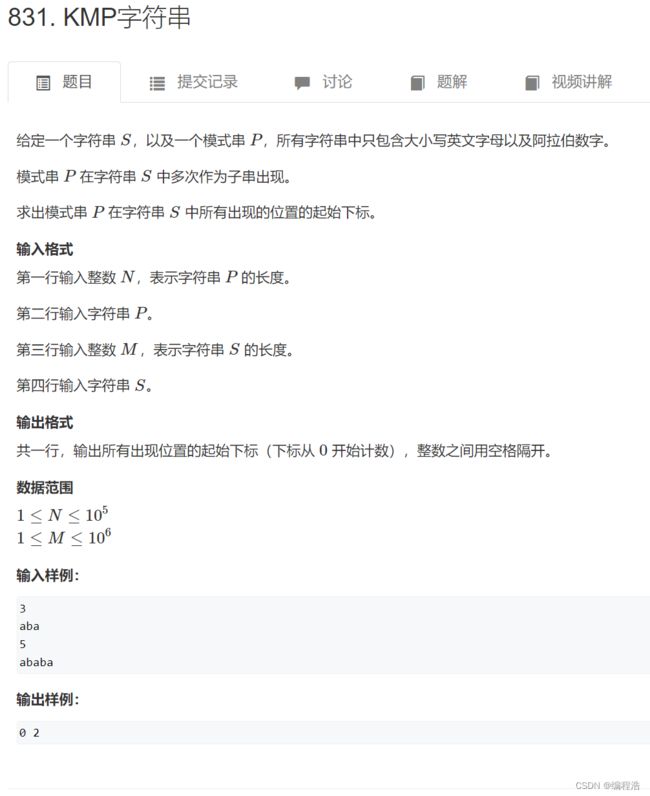
十一、KMP
KMP是快速帮助 子串A 去匹配 主串B的算法
我们利用next记录
当B和A不匹配的时候,A应该返回B中的哪个位置
所以next应该记录的是B的快速匹配位置
具体逻辑可以搜CSDN
#include 十二、排序
1. 快速排序
- 快速排序的核心思想是:
大于x的 放到数组右边
小于x的放在数组左边
等于x的放在数组中间 - 剩下的背模板即可
#include2. 整数集合划分
#include 十三、多路归并
1. 三元组的最小距离(2020年全国硕士研究生招生考试)


什么是多路归并?
就是三个数组排序到一个数组进行比较
是需要开一个数组的空间的
为了节约空间,我们可以通过三个数组分别用三个指针
指向各自数组,然后判断当前三个元素的大小关系以及进行相应的运算或者应用数据去计算,之后根据三个元素的大小关系进行角标转移
放到本题中
首先我们要理解题意
题意是让我们求三个数组中放到一个数组排序后,出现的最小值到最大值距离最短的是多少
比如
a b c之间满足
最小值a 到 最大值c距离最小
并且之间包含b数组的元素
或者是
b a c也可以
总之就是
最小值和最大值并且中间包含一个与这两个集合不一样的集合元素
的距离值 ✖ 2就是答案
#include