《信号与系统》——连续傅里叶变换与拉布拉斯变换专题
公众号公式总结
信号与系统:研究时域连续的模拟信号
- 一、线性时不变系统(LTI)
-
- 3.1 我们研究的是什么
-
- 信号
- LTI系统
- 卷积、微分方程、差分方程
- 系统函数
- 3.3常见的RC滤波器与电路
-
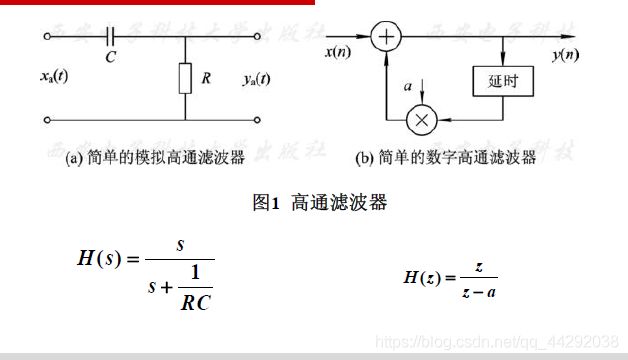
- 高通滤波器
- 低通滤波器
- 带通滤波器
- 二、连续傅里叶变换
-
- 1.连续周期信号傅里叶级数(FS)——频谱F(nw1)
- 2.连续周期信号傅里叶变换(FT)————频谱密度函数F(w)
-
- 周期单位冲击信号的FT
- 3.连续非周期信号傅里叶变换(FT)————频谱密度函数F(w)
-
- 3.1傅里叶变换的性质
- 3.2傅里叶级数与非周期傅里叶变换系数互求
- 4.常用小公式
-
- 抽样信号
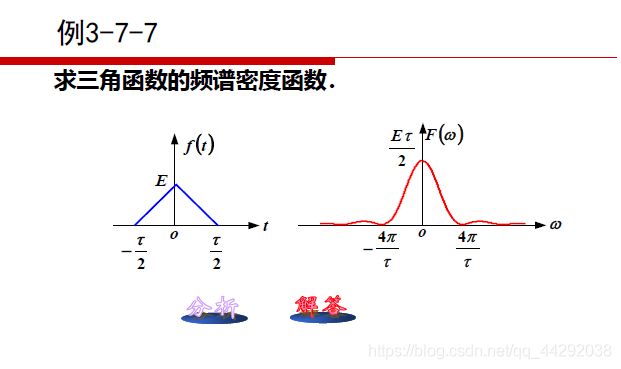
- 三角波信号的FT
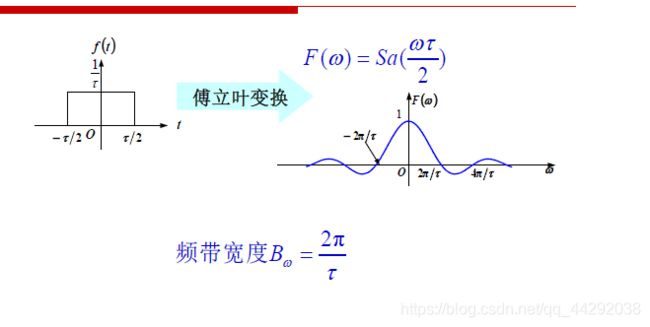
- 矩形信号 (门函数、窗函数)的FT
- 频域矩形信号的傅里叶反变换
- 周期矩形信号的傅里叶级数
- 周期矩形信号的FT
- 5.其他常见信号的傅里叶变换
-
- 欧拉公式
-
- 复指数信号、三角函数的FT
- 冲击信号、冲击偶信号的FT
- 直流信号的FT
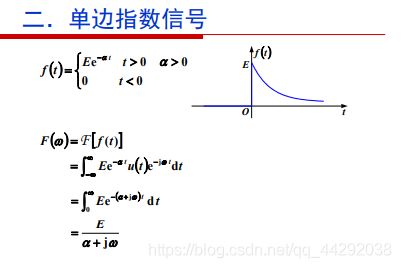
- 单边指数信号
- 双边指数信号
- 符号函数
- 单位阶跃函数u(t)
- 三、拉普拉斯变换
-
- 拉普拉斯变换与傅里叶变换
- 2.1拉普拉斯变换的定义
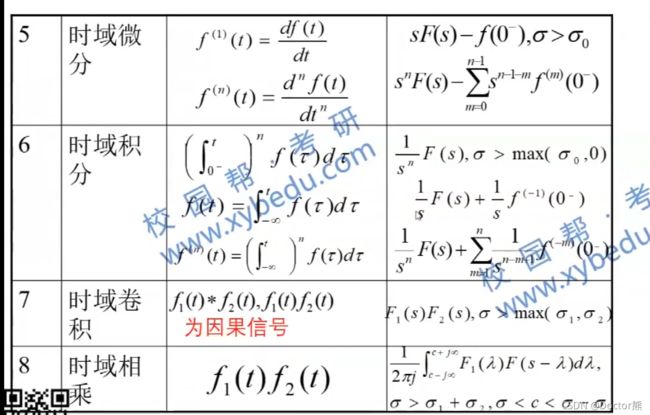
- 2.2拉普拉斯变换的性质
- 2.3 H(s)零极点分布决定系统单位冲击响应h(t)时域特性
- 2.3 H(s)零极点分布判断系统的频响特性H(jw)
- 四、简单z变换
一、线性时不变系统(LTI)
3.1 我们研究的是什么
信号
无限长的信号:
理论研究中存在而现实中没有,其中研究最多的是周期信号
有限长的信号:
满足绝对可和的非周期信号是傅里叶变换的研究重点
LTI系统
系统就是函数
不同之处在于函数研究对于不同的自变量取值因变量是什么样的
系统多了一个自变量时间,系统输入输出的变量都自带时间属性
也可以说是研究两个因变量之间的函数关系
线性系统:y(t)=kx(t),x(t)扩大多少倍,y(t)就扩大多少倍,且可以叠加
正比例函数:y=kx,自变量x扩大多少倍,因变量就扩大多少倍,且可以叠加
时不变系统:输入波形平移多少,输出波形就平移多少
输入波形从0到第5秒,输出波形是1到第6秒
则若在第6秒再次输入波形,输出波形在第7秒再次出现
卷积、微分方程、差分方程
连续卷积与离散卷积
解方程专题(各学科:高数、线代、专业课)
系统函数
3.3常见的RC滤波器与电路
电容通高频阻低阻,通交流隔直流
在基本的RC滤波电路中:C做输出端就是低通滤波器,R做输出就是高通滤波器
考虑一个连续的过程,当电源频率由0变大时,电阻逐渐分压
在高通电路中,电阻两端的电压由0慢慢变大,因而高通
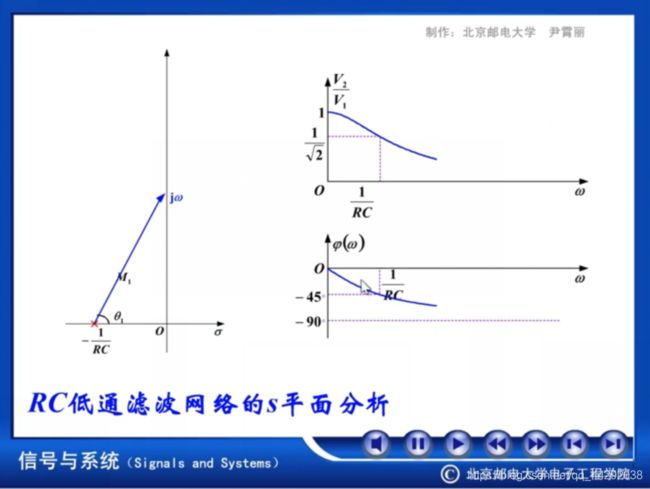
而在低通电路中,电容两端电压由大变小,因而低通
基本原理是,当电容和电阻串联时
若电源为直流电(f=0 ),由于电容的隔直作用,故只有电容两端有电压,而电阻两端的电压为0,
若电源为交流电(f>0 ),电容导通,频率越高导通阻抗越小,因而高通
高通滤波器
低通滤波器
带通滤波器
二、连续傅里叶变换
1.连续周期信号傅里叶级数(FS)——频谱F(nw1)


有幅度频谱图与相位频谱图


周期越大,频谱越密集
复数F(nw1)=信号余弦分量实部+信号正弦分量虚部
偶函数傅里叶级数不含正弦项,F(nw1)为实函数(幅度谱就是频谱)
奇函数傅里叶级数不含余弦项,F(nw1)为虚函数
2.连续周期信号傅里叶变换(FT)————频谱密度函数F(w)
注:
理论上只有满足绝对可和条件的非周期信号才能傅里叶变换
不满足绝对可和条件的非周期信号无法进行傅里叶变换
不满足绝对可和条件的周期信号(不绝对可和)无法进行傅里叶变换
实际中因为正余弦周期信号都有傅里叶变换,普通周期信号可以先求傅里叶级数转化成很多正弦信号的和,再对傅里叶级数傅里叶变换
周期单位冲击信号的FT
3.连续非周期信号傅里叶变换(FT)————频谱密度函数F(w)
物理意义:f(t)分解成无穷多个连续的频率不同的振幅无穷小的正弦信号
——在某个具体频率w处频谱是1/TF(w)= F(w)dw/2pi,T是无穷大周期
频谱1/TF(w)无穷小,频谱密度F(w)有限值



3.1傅里叶变换的性质

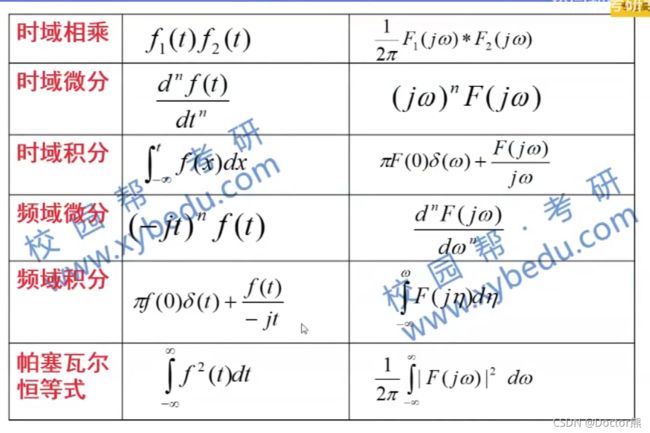
8.奇偶虚实性
f(t)偶函数,只有R(w),相位±兀
f(t)偶函数,只有X(w),相位±兀/2
3.2傅里叶级数与非周期傅里叶变换系数互求
非周期如果当做是周期的一部分
非周期傅里叶变换除以有限长度,得到周期信号傅里叶级数系数!(周期频谱)
非周期傅里叶变换除以无限长度,得到非周期傅里叶级数系数!(非周期频谱)
求周期傅里叶变换:3步
1.求非周期傅里叶变换
2.求周期傅里叶级数(上面的转换法)
周期的傅里叶变换系数F(nw1)=非周期的傅里叶变换F(w)除以有限周期(w换成nw1)
3.求周期傅里叶变换:对级数形式做傅里叶变换
F T ( ω ) = 级 数 和 F ( n w 1 ) 乘 以 2 π δ ( w − n w 1 ) ) F _T(ω)=级数和F(nw1)乘以2\pi\delta(w-nw_1)) FT(ω)=级数和F(nw1)乘以2πδ(w−nw1))
?有点像那个能量、功率信号那个意思

4.常用小公式
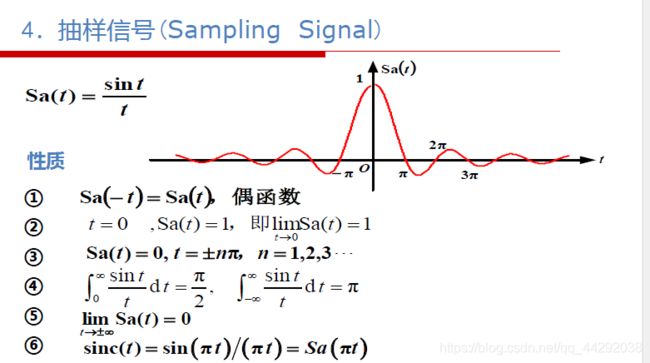
抽样信号
三角波信号的FT
矩形信号 (门函数、窗函数)的FT
频域矩形信号的傅里叶反变换
周期矩形信号的傅里叶级数
周期矩形信号的FT
5.其他常见信号的傅里叶变换
欧拉公式
复指数信号、三角函数的FT
e j w 0 t < — — > 2 π δ ( w − w 0 ) e^{jw_0t}<——>2\pi\delta(w-w_0) ejw0t<——>2πδ(w−w0)
e − j w 0 t < — — > 2 π δ ( w + w 0 ) e^{-jw_0t}<——>2\pi\delta(w+w_0) e−jw0t<——>2πδ(w+w0)
c o s w 0 t < — — > π [ δ ( w + w 0 ) + δ ( w − w 0 ) ] cosw_0t<——>\pi[\delta(w+w_0)+\delta(w-w_0)] cosw0t<——>π[δ(w+w0)+δ(w−w0)]
s i n w 0 t < — — > j π [ δ ( w + w 0 ) − δ ( w − w 0 ) ] sinw_0t<——>j\pi[\delta(w+w_0)-\delta(w-w_0)] sinw0t<——>jπ[δ(w+w0)−δ(w−w0)]
冲击信号、冲击偶信号的FT
δ ( t ) < — — > 1 \delta(t)<——>1 δ(t)<——>1
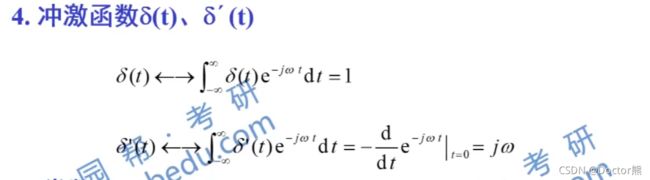

直流信号的FT
1 < — — > 2 π δ ( w ) 1<——>2\pi\delta(w) 1<——>2πδ(w)
E < — — > 2 π E δ ( w ) E<——>2\pi E\delta(w) E<——>2πEδ(w)
单边指数信号
双边指数信号
其他推导链接
符号函数
单位阶跃函数u(t)
三、拉普拉斯变换
拉普拉斯变换与傅里叶变换
2.1拉普拉斯变换的定义
拉普拉斯变换是给信号指数级衰减(大小收敛域实部),信号进行傅里叶变换的结果
收敛域是给信号收敛域实部对应的衰减可以使信号收敛的区域
极点是使信号拉普拉斯变换结果趋向无穷的点,变换的结果不是有限值
s负半平面是给信号增长趋势,极点位于左半平面说明给信号一定程度的增长都可以使得信号收敛
s正半平面是给衰减衰减趋势,极点位于右半平面必须给予信号衰减才能使得信号收敛
s=0是不对信号做变化,极点在原点信号不收敛,应该衰减才能使信号收敛
2.2拉普拉斯变换的性质
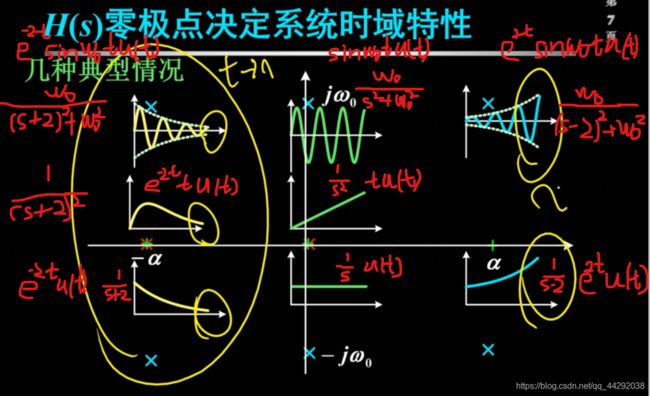
2.3 H(s)零极点分布决定系统单位冲击响应h(t)时域特性
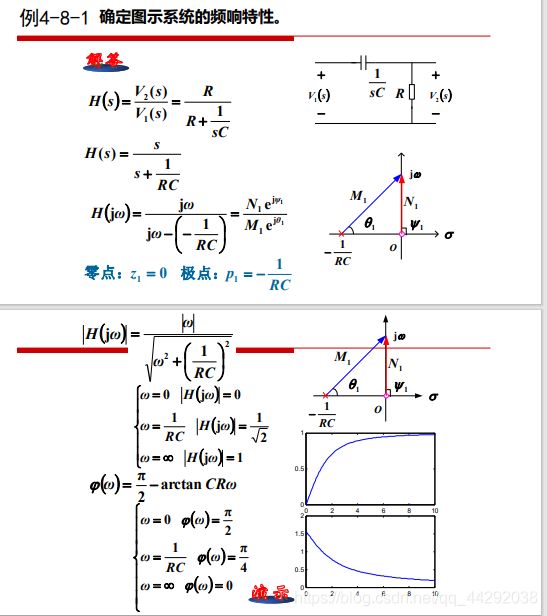
2.3 H(s)零极点分布判断系统的频响特性H(jw)
H(jw)变换成零极点类型,根据零极点大致判断H(jw)的频响特性曲线
s复平面两种形式:直角坐标,极坐标
jw是在虚轴上移动的点,从0到正无穷
分子变成零点矢量,由零点指向虚轴上的点
分母变成极点矢量,由极点指向虚轴上的点