【数据结构】:二叉树,线索二叉树,排序二叉树,AVL树
文章目录
- 前言
- 一 二叉树
-
- 0)二叉树较为重要的种类
-
- 1. 满二叉树
- 2.完全二叉树
- 1) 二叉树的存储结构
- 2) 初始化二叉树
- 3)创建二叉树
-
- 1.创建二叉树的方式 1
- 2.创建二叉树 2
- 3.创建二叉树 3
- 4)遍历二叉树
-
- 1.前序递归遍历
- 2.中序递归遍历
- 3.后序递归遍历
- 4.层次遍历
- 5. 前序非递归遍历
- 6. 中序非递归遍历
- 7. 后序非递归遍历。
- 5)二叉树的常用方法实现
-
- 1.二叉树的结点数
- 2.二叉树的高度
- 3. 查找二叉树某个结点
- 4.查找二叉树某个结点的父结点
- 5.二叉树的镜像
- 二 线索二叉树
-
- 0)线索化二叉树的存储结构
- 1)初始化线索二叉树
- 2)创建线索化二叉树
- 三 二叉排序树(二叉搜索树)
-
- 0)二叉排序树的存储结构
- 1)二叉排序树的插入
- 2)二叉排序树的常用操作
-
- 1. 二叉排序树节点的最小值
- 2.二叉排序树节点的最大值
- 3.二叉排序树的查找
- 4.二叉排序树的删除
- 四 平衡二叉树(AVL)
-
- 0)AVL树相关的基本概念
- 1)平衡二叉树的存储结构
- 2)初始化平衡二叉树
- 3)平衡二叉树的插入
-
- 1.插入
- 2.右旋转
- 3.左旋转
- 4.先左后右旋转
- 5.先右后左旋转
- 寄语
前言
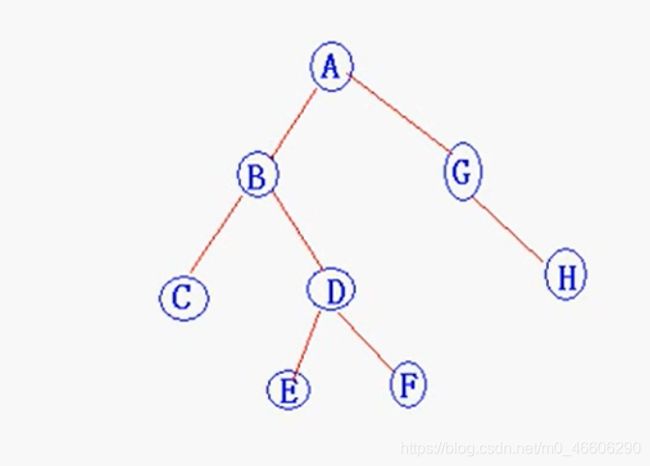
二叉树分好多种:
我在这里分享四种二叉树的基本操作集合。
- 普通的二叉树(二叉树)
- 线索二叉树
- 搜索二叉树(二叉排序树)
- 平衡(AVL)二叉树
一 二叉树
0)二叉树较为重要的种类
满二叉树和完全二叉树。
1. 满二叉树
一棵二叉树,除了叶子节点的度为0,其余所有节点的度都为2,与此同时,叶子节点都在同一层上。
如图:
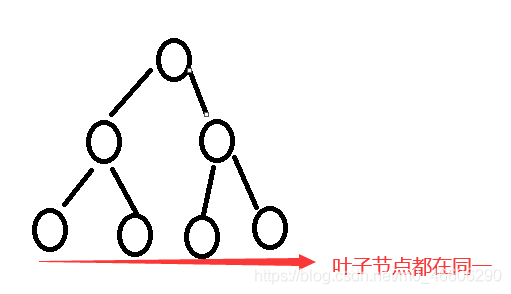
性质:n层,有 2n-1 个节点。
类似于一个细胞无线分裂的感觉哈哈哈。
2.完全二叉树
完全二叉树:就是从根节点开始数,从左往右按层数,不断结点就算是了。

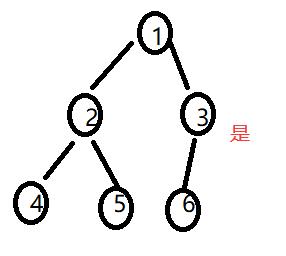

知道什么样子是完全二叉树就行了。
1) 二叉树的存储结构
二叉树两种存储结构,一种是顺序存储结构,一种是链式存储结构,由于前者有一定的缺陷,我就主要讲讲链式存储结构的二叉树,这也是最普遍的存储结构方式。有人会问我,为啥顺序存储二叉树会有缺陷,其实顺序存储结构就对完全二叉树比较友好,能够利用好空间,而对于存储其他的二叉树,就不友好了,往往会浪费大量空间,平时我们的二叉树不是完全二叉树的概率很大,所以不用顺序存储结构啦。废话不多说,冲。
二叉树链式存储结构:
#define ElemType char
// 定义二叉树的节点类型
typedef struct BinTreeNode
{ //数据域
ElemType date;
//指针域
BinTreeNode* lChlid; //左孩子指针
BinTreeNode* rChlid; //有孩子指针
}BinTreeNode;
// 定义二叉树类型
typedef struct BinTree
{
BinTreeNode* root; //指向二叉树节点的根节点
ElemType refvalue; //创建二叉树的结束标志
}BinTree;
咳咳,我解释以下,这个存储结构看似很复杂,其实不然,对于BinTreeNode 类型,就是数据域和指针域,只不过指针域有两个了,和之前我们定义单链表的结构类似,都是从单链表引入过来的。

那为什么还要定义一个 BinTree 二叉树类型呀。咳咳,因为等会我们要创建二叉树嘛,一个二叉树最重要的就是 root 根,只要根还在,树就还在,看它如此重要就给它搞个类型BinTree咯。加个refvalue就表示结束标志,怎么理解呢,就一会你创建二叉树时候,难道你要你的二叉树一直生孩子嘛?那不会吧,不会吧。哈哈哈,所以送它一个refvalue 结束标志的东西,让节点指向这个东西就结束,不继续指向下去了。

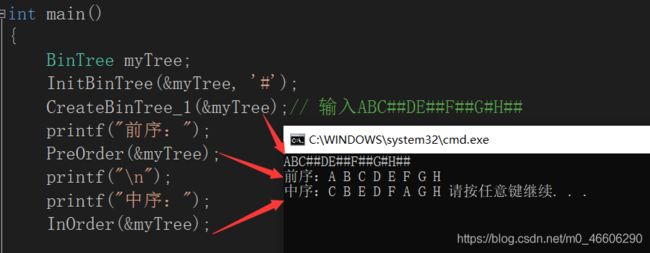
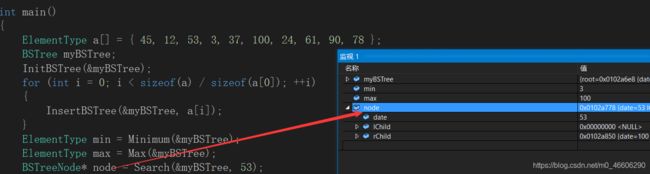
我们在main函数里面定义一个BinTree myTree;对于myTree 变量;vs2013测试如下:
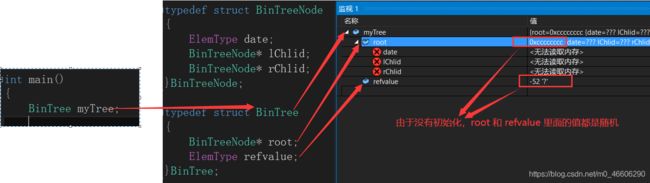
不知道会不会有人在想,BinTreeNode 类型里面的 date , lChild, rChlid 都是有个红色叉叉的?其实很正常,你定义的是BinTree类型的变量,不是BinTreeNode 类型的变量,只有在定义了变量的地方才会分配有内存空间,你都没定义肯定没有分配内存空间啦,没有内存空间人家就给你打个红色叉叉表示咯。
啰里啰唆那么多,只想说明这个存储结构重要呀,希望我讲明白了。那接下来自然而然就是初始化二叉树咯。
2) 初始化二叉树
void InitBinTree(BinTree* bt, ElemType ref)
{
bt->root = NULL;
bt->refvalue = ref;
}
初始化很简单滴,把root先指向空,防止野指针,然后传个结束标志变量 ref初始化refvalude就可以。我们把根 root 指向 NULL 的树叫空树。
测试图:
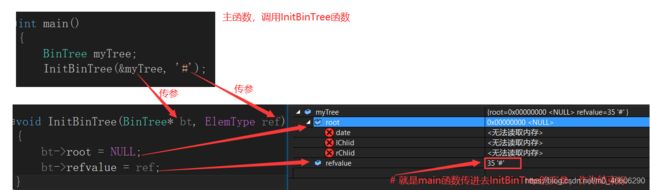
3)创建二叉树
创建二叉树的方式有很多种,我提供三种方式供你们使用。
1.创建二叉树的方式 1
//对外的实际接口函数
void CreateBinTree_1(BinTree* bt)
{
CreateBinTree_1_(bt, &(bt->root));
}
//二叉树创建的真实实现函数。
void CreateBinTree_1_(BinTree* bt, BinTreeNode** t) //传二级指针的目的是为了修改lchild,rchild两个指针的指向
{
//输入字符,来创建二叉树。
//输入ABC##DE##F##G#H##
ElemType item;
scanf("%c", &item);
if (item == bt->refvalue) //若输入的字符为 ‘#’,就给该节点赋值空
(*t) = NULL;
else
{ //否则,字符不是‘#’,则为该节点分配空间
(*t) = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert((*t) != NULL);
(*t)->date = item;
//递归调用左孩子,为其创建节点
CreateBinTree_1_(bt, &((*t)->lChlid));
//递归调用右孩子,为其创建节点
CreateBinTree_1_(bt, &((*t)->rChlid));
}
}
2.创建二叉树 2
//对外的实际接口函数
void CreateBinTree_2(BinTree* bt)
{
bt->root = CreateBinTree_2_(bt);
}
//二叉树创建的真实实现函数。
BinTreeNode* CreateBinTree_2_(BinTree* bt)
{
ElemType item;
scanf("%c", &item);
//输入ABC##DE##F##G#H##
if (item == bt->refvalue)
return NULL;
else
{
BinTreeNode* t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t);
t->date = item;
t->lChlid = CreateBinTree_2_(bt);
t->rChlid = CreateBinTree_2_(bt);
//把创建好的节点返回
return t;
}
}
和第一种测试结果是一样的,只是实现方式有点不同,这里是直接返回根root 节点。好好体会两种的区别。
3.创建二叉树 3
//对外的实际接口函数 ,通过外部传入的字符 str 来创建二叉树
//传入str = ABC##DE##F##G#H##
//这里用到了c++中引用的方式来传参str
void CreateBinTree_3(BinTree* bt, char*& str)
{
CreateBinTree_3_(bt, bt->root,str);
}
//二叉树创建的真实实现函数。
void CreateBinTree_3_(BinTree* bt, BinTreeNode*& t, char*& str)
{ //*str 就表示 每一个字符。不是字符串哦。
if (*str == bt->refvalue)
t = NULL;
else
{
t =(BinTreeNode*)malloc(sizeof(BinTreeNode));
t->date = *str;
CreateBinTree_3_(bt, t->lChlid, ++str); //注意str 是指针,需要先++,后移
CreateBinTree_3_(bt, t->rChlid, ++str);
}
}
这里多了一点不同的地方就多了一个直接传参str字符串,这样避免了每次调用函数都需要输入字符串的麻烦咯。测试代码也是一模一样的。
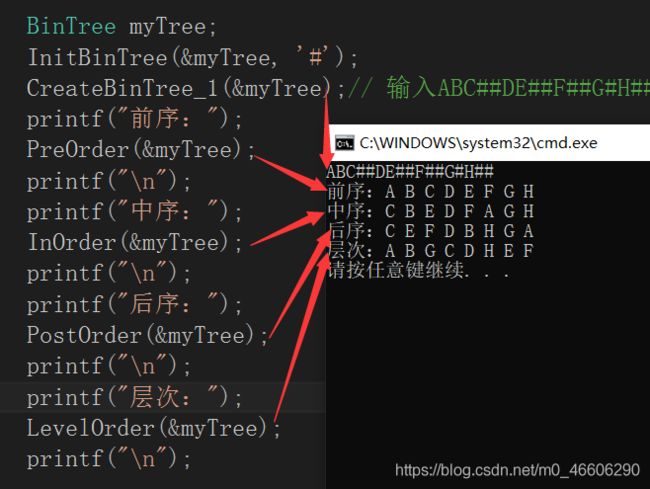
主函数输入就可以自己测试下咯:
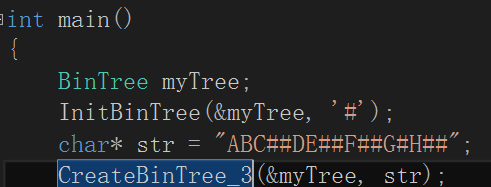
好咯,创建好二叉树最主要的还是为了遍历二叉树。接下来我就讲遍历二叉树。
- 递归遍历二叉树
- 前序递归
- 中序递归
- 后序递归
- 非递归遍历二叉树
1.利用栈 实现前中后遍历
2.利用队列实现层次遍历
4)遍历二叉树
遍历二叉树就是,从根结点开始访问,所有节点都当且仅当访问一次。
1.前序递归遍历
先访问根,再访问左子树,最后访问右子树。
void PreOrder(BinTree* bt)//对外接口
{
PreOrder_(bt->root);
}
void PreOrder_(BinTreeNode* t)
{
if (t != NULL)
{
printf("%c ", t->date); //访问根
PreOrder_(t->lChlid);
PreOrder_(t->rChlid);
}
}
2.中序递归遍历
先访问左结点,再访问根结点,最后访问右结点。
void InOrder(BinTree* bt)//对外接口
{
InOrder_(bt->root);
}
void InOrder_(BinTreeNode* t)
{
if (t != NULL)
{
InOrder_(t->lChlid);
printf("%c ", t->date);
InOrder_(t->rChlid);
}
}
3.后序递归遍历
也就是先访问左结点,再访问右结点,最后访问根节点。
void PostOrder(BinTree* bt) //对外接口
{
PostOrder_(bt->root);
}
void PostOrder_(BinTreeNode* t)
{
if (t != NULL)
{
PostOrder_(t->lChlid);
PostOrder_(t->rChlid);
printf("%c ", t->date);
}
}
4.层次遍历
层次遍历就是一层一层的访问结点,不过层次遍历要借助队列的帮助。我们调入链队来帮助我们完成层次遍历。不知道队列是什么可看看我之前的文章(数据结构第六篇(1):线性表之链式队列)。要把 #define Elemtype int 改成 #define Elemtype BinTreeNode*。
void LevelOrder(BinTree* bt)
{
LevelOrder(bt->root);
}
void LevelOrder(BinTreeNode* t)
{ //节点不空就入队
if (t != NULL)
{
LinkQueue Q;
InitQueue(&Q);
//入队,入的是结点
EnQueue(&Q, t);
BinTreeNode* v; //创建变量v接收获取的队头结点
// 队不空就获取队头元素。
while ( !QueueIsEmpty(&Q) )
{
GetQueue(&Q,&v);
printf("%c ", v->date);
// 访问完根就入队左结点,前提左结点不空
if (v->lChlid)
EnQueue(&Q, v->lChlid);
// 访问完根或者左结点后就入队右结点,前提右结点不空
if (v->rChlid)
EnQueue(&Q, v->rChlid);
}
}
}
5. 前序非递归遍历
由于非递归版本用c实现起来有点复杂,我们可以用c实现,可是不太好理解,这里我就要c++中的一点点知识去辅助c实现,其实和c没什么区别,只是写法上会简单一点。
非递归遍历需要借助栈结构,如果对栈又不知道的可以看看我之前的文章:数据结构第五篇:线性表之顺序栈。
记住一点,非递归不要害怕。都是前序,就是访问顺序为,中左右。
void PreOrder (BinTreeNode* node)
{
if (node == NULL)
return;
stack<BinTreeNode*> S;
printf("%c ",node->date); //先访问根节点。
S.push(node); /入栈,入根
node = node->left;
while (!S.empty() || node != NULL)
{
while(node)
{
printf("%c",node->date);
S.push(node);
node = node -> left;
}
}
//直到左子树访问结束后退出循环,继续访问右树;
node = S.top() -> right;
S.pop();
}
过程:
- 输出 A ,A 入栈,node指向A左结点B;
- 输出 B ,B 入栈,node指向B左结点C;
- 输出 C ,C 入栈,node指向C左结点NULL;
- node 指向C右节点为NULL,出栈C;
- node回退到了B,指向B的右节点D,出栈B;
- 输出 D,D 入栈,node指向D左结点E;
- 输出 E,E 入栈,node指向E左结点NULL;
- node指向E右节点为NULL,出栈E;
- node回退到D,指向D的右节点F,出栈D;
- 输出F,F入栈,node指向F左结点NULL;
- node 指向F右节点为NULL,出栈F;
- 。。。
- 一直循环直到输出完毕。
6. 中序非递归遍历
访问顺序左中右;
void InOrder(BinTreeNode* node)
{
if (node == NULL)
return;
stack <BinTreeNode* > S;
S.push(node);
node = node->lChlid;
while (!S.empty() || node != NULL)
{ //先遍历左子树
while (node)
{
S.push(node);
node = node->lChlid;
}
// 输出节点
printf("%c ", node->date);
// 遍历右子树
node = S.top()->rChlid;
S.pop();
}
}
- 入栈A,node指向A的左子树B;
- 入栈B,node指向B的左子树C;
- 入栈C,node指向C的左子树NULL;
- 输出C,node指向C的右子树NULL;
- C出栈,输出B,node指向B的右子树D;
- 入栈D,node指向D的左子树E;
- 入栈E,node指向E的左子树NULL;
- 输出E,node指向E的右子树NULL;
- E出栈,输出D,node指向D的右子树F;
- …
- 反复循环,直到遍历完。
7. 后序非递归遍历。
后序非递归我们可以借助两个栈来实现,其实不难,记住访问顺序左中右。
void PosOrder(BinTreeNode* node)
{
if (root == NULL)
return;
//定义栈 s,用来遍历节点,output栈用来访问节点
stack<BinTreeNode*> s, output;
S.push(node);
while (!S.empty())
{
BinTreeNode* cur = S.top();
output.push(cur);
S.pop();
if (cur->lChlid)
S.push(cur->lChlid);
if (cur->rChlid);
S.push(cur->rChlid);
}
//访问结点,
While(!output.empty())
{
printf("%c", output.top()->date);
out.pop();
}
}
过程:
由于访问顺序为左中右,所以入栈output中就要中左右,这样才会保证出栈时候是左中右。
- 入A结点 到S中,再从S栈中入到output栈中。
- 再入A的左树和右树到S栈中。
- 重复上述步骤,直到output栈入完结点。
- 最后输出output栈的结点。
5)二叉树的常用方法实现
常用的方法有:
- 二叉树的结点数
- 二叉树的深度
- 查找某个结点
- 查找某个结点的父结点
- 二叉树的镜像
…
这里就先提供这些常用的方法,大家以后刷题碰到再看看其他的。
1.二叉树的结点数
int Count(BinTreeNode* node)
{
if(node == NULL)
return ;
else
{ //左子树的节点数加右子树的结点数加根结点。
return count(node->lChild) + count(node->rChild) +1;
}
}
2.二叉树的高度
void Height(BinTreeNode* node)
{
if(node == NULL)
return;
//计算左子树的高度
int leftHeight = Height(node->lChild);
//计算右子树的高度
int rightHeight = Height(node->rChild);
// 若返回大的树高度加根的数。
return (LeftHeight > rightHeight ? leftHeight : rightHeight) +1;
}
3. 查找二叉树某个结点
查找到返回该结点,不是返回该
BinTreeNode* Search(BinTreeNode* node, ElementType key)
{ //若为空树直接返回
if (node == NULL)
return NULL;
//若根结点为key值,直接匹配成功
if (t->date == key)
return t;
//开始匹配左结点
BinTreeNode *left_Node = Search_1(t->leftChild, key);
if (left_Node != NULL) //找到了,就返回
return left_Node;
//左子树没匹配成功就匹配右子树
return Search_1(t->rightChild, key);
}
4.查找二叉树某个结点的父结点
BinTreeNode* SearchParent_1(BinTreeNode* t, BinTreeNode* node) //t为树,node为要查找的结点
{ //若树为空 或者查找的结点为NULL,直接返回
if (t == NULL || node == NULL)
return NULL;
if (t->leftChild == node ||t->rightChild == node) //若为查找的树为根节点,直接返回根节点
return;
//递归查找t中左子树的node的父节点
BinTreeNode* cur = SearchParent_1(t->leftChild, node);
if (cur != NULL)
return cur;
//若t中的左子树没有node 的父节点 则在t中的右子树找
//递归查找t中右子树的node的父节点
return SearchParent_1(t->rightChild, node);
}
5.二叉树的镜像
镜像的意思就是,对称。我们只要以根为对称轴,交换左右结点就可以求出镜像树了。
void Mirror (BinTreeNode* t)
{
BinTreeNode* temp;
temp = t->lChild;
t->lChild = t->rChild;
t->rChild = temp;
//递归调动左右子树
Mirror(t->lChild);
Mirror(r->rChild);
}
好了,进入第二个主题:线索二叉树
二 线索二叉树
- 什么是线索二叉树?
线索二叉树就是,在二叉树的基础上添加了标记结点,来标记指向前驱结点和后继结点的指针。
2.为什么会有线索二叉树?
这是因为,二叉树在遍历时候才可以直到结点的前驱和后继,创建时候并不能知道其某个结点的前驱后继,而我们希望能在创建二叉树的时候就能直到某个节点的前驱后继,这样能够大大减少时间,所以引出了线索二叉树。
3.线索二叉树如何标记结点指向前驱和后继?
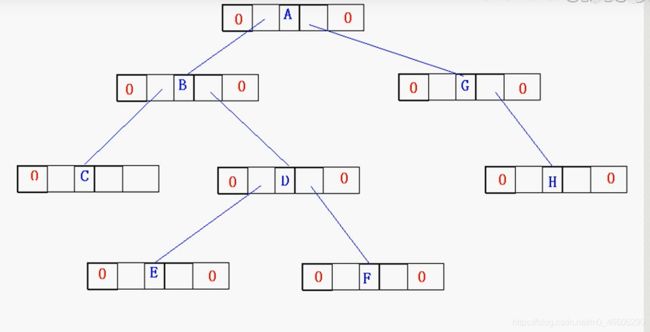
如何形象的理解线索二叉树?
线索化后的二叉树(中序遍历的前提下的)
C E D F B A G H
比如我要找E的前驱,E的左标记为1,则指向其前驱为B,E的后继,E的右标记为1,其前驱就是D.但,要找D的前驱和后继却找不出来,这就说明线索化二叉树并不都是可以找出所有结点的前驱和后继的。如何解决这个问题?先留个悬念。
0)线索化二叉树的存储结构
typedef char ElementType;
//LINK(链) 表示 0;指向真实的左右孩子。
//THREAD(线索) 表示 1;指向前驱和后继。
typedef enum{LINK, THREAD} TagType;
//线索二叉树结点类型
typedef struct ThrBinTreeNode
{
ElementType date;
struct ThrBinTreeNode* leftChild;
struct ThrBinTreeNode* rightChild;
TagType leftTag; //左标记
TagType rightTag; //右标记
}ThrBinTreeNode;
//线索二叉树类型
typedef struct ThrBinTree
{
ThrBinTreeNode* root;
ElementType refvaule;
}ThrBinTree;
线索化二叉树就是在二叉树的基础上多了左右标记结点。
1)初始化线索二叉树
void InitThrBinTree(ThrBinTree* bt)
{
bt->root = NULL;
bt->refvaule = '#';
}
2)创建线索化二叉树
线索化二叉树的前提要有二叉树哦。
通过外部传入字符串来创建二叉树先。
void CreateThrBinTree(ThrBinTree* bt, char* str)
{
CreateThrBinTree_(bt, bt->root, str);
}
void CreateThrBinTree_(ThrBinTree* bt, ThrBinTreeNode*& t, char*& str)
{
if (bt->refvaule == *str)
t = NULL;
else
{
t = (ThrBinTreeNode*)malloc(sizeof(ThrBinTreeNode));
t->date = *str;
t->leftChild = NULL;
t->rightChild = NULL;
t->leftTag = LINK;
t->rightTag = LINK;
CreateThrBinTree_(bt, t->leftChild, ++str);
CreateThrBinTree_(bt, t->rightChild,++str);
}
}
创建线索线索化二叉树:
void Create(ThrBinTree* bt)
{
ThrBinTreeNode* pre = NULL;
Create(bt->root,pre);
//当pre指向最后一个节点时候,单独线索化
pre->rightChild = NULL;
pre->rightTag = THREAD;
}
void Create(ThrBinTreeNode* &t, ThrBinTreeNode* &pre)
{
if (t = NULL)
return;
//先线索化t的左树;
Create(t->leftChild, pre);
//线索化都是对空指针线索化
if (t->leftChild == NULL)
{
t->leftTag = THREAD;
t->leftChild = pre;
}
if (pre != NULL && pre->rightChild == NULL)
{
pre->rightTag = THREAD;
pre->rightChild = t;
}
//pre为空时候使其指向t
pre = t;
Create(t->rightChild, pre);
}
其实本质中序也是左中右的访问顺序,先先递归调动线索化左子树,然后把之前二叉树打印换成了现在的线索化操作,最后递归调动右子树线索化。
三 二叉排序树(二叉搜索树)
- 有排序两个字,说明这个树就是按某种顺序排序好的,那按什么顺序排序好的呢?
- 为什么会有二叉排序树?
在数据结构中,很多莫名其妙的东西被搞出来,自然有它存在的道理,那二叉排序树存在的到了是什么呢?那就是为了提升查找效率呀。举个例子对于上图的二叉排序树,假如我们要找78这个数,我们只要拿78和根的值45比较,就可以断定,78 一定在右数,而不在左树,这样就不用挨个去左树找。会节省很多时间。
0)二叉排序树的存储结构
我们要清楚,二叉树的其他变形的树,都是在二叉树的基础上来的。
typedef int ElementType;
typedef struct BSTreeNode
{
ElementType date; //数据域
//指针域
struct BSTreeNode* lChild;
struct BSTreeNode* rChild;
}BSTreeNode; //二叉排序树结点类型
typedef struct BSTree
{
struct BSTreeNode* root;
}BSTree; //二叉排序树类型
和普通的二叉树没什么区别。BSTree 是binary sort tree(二叉排序树)的意思。
1)二叉排序树的插入
插入成功返回 1,失败返回 0
//对外函数的接口
bool InsertBSTree(BSTree* node, ElementType x)
{
return InsertBSTree_(&node->root, x);
}
//内部函数的真实实现
bool InsertBSTree_(BSTreeNode** node, ElementType x)
//因为插入数据需要修改类型的指针域,所以传二级指针。
//为了使内部函数对指针的修改能够影响外部的指针域
{
if (*node == NULL) //插入根结点
{
*node =(BSTreeNode*) malloc(sizeof(BSTreeNode));
(*node)->date = x;
(*node)->lChild = NULL;
(*node)->rChild = NULL;
//返回1表示插入成功
return 1;
}
//插入的数x比date小,则插入左子树
else if (x <(*node)->date)
{
InsertBSTree_(&(*node)->lChild, x);
}
//插入的数x比date大,则插入右子树
else if (x>(*node)->date)
{
InsertBSTree_(&(*node)->rChild, x);
}
//x与date相等返回0表示插入失败
return 0;
}
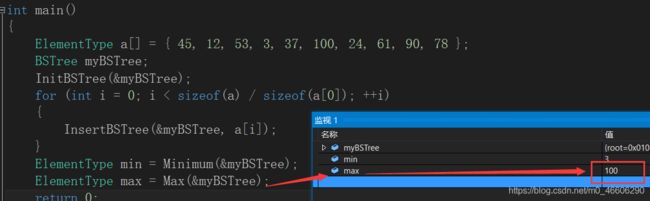
测试数据:
也是上诉图的二叉排序树数据。

调试结果:
测试也测试完了,可是我们好像还是不太懂怎么表示算是排序完了,看着乱七八糟的,不急我给你看个图,把二叉排序树做一点小操作就变成了线性的排序模样了。
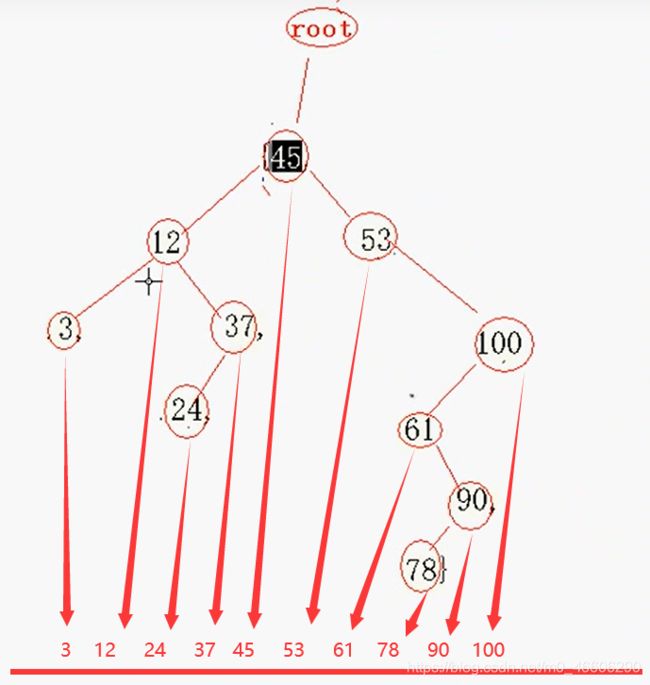
你说神不神奇。是不是给你排序好了咯。这只是直观的感觉啦。只要我们进行中序遍历,就得到了这排序的数据。
这个排序二叉树有什么方便的呢?看看下面的操作就行。
2)二叉排序树的常用操作
1. 二叉排序树节点的最小值
求二叉排序树的结点最小值,很容易求,只要找到最左边的那一个结点就可以咯。
ElementType Minimum(BSTree* bt)
{
assert(bt);
return Minimum_(bt->root);
}
ElementType Minimum_(BSTreeNode* node)
{
while (node->lChild != NULL)
{
node = node->lChild;
}
//退出循环后到达最左边的树
return node->date;
}
2.二叉排序树节点的最大值
一直遍历到最右边的右子树就可以咯。
ElementType Max(BSTree* bt)
{
assert(bt);
return Max_(bt->root);
}
ElementType Max_(BSTreeNode* node)
{
while (node->rChild != NULL)
node = node->rChild;
return node->date;
}
3.二叉排序树的查找
给定一个key值,去二叉排序树中找该值,找到返回结点,找不到返回NULL。
BSTreeNode* Search(BSTree* bt, ElementType key)
{
return Search_(bt->root, key);
}
BSTreeNode* Search_(BSTreeNode* node, ElementType key)
{
if (node == NULL)//空树直接返回
return NULL;
if (node->date == key) //查找的值为根节点
return node;
else if (key < node->date)
return Search_(node->lChild, key);
else if (key > node->date)
return Search_(node->rChild, key);
}
4.二叉排序树的删除
二叉排序树的删除不是删除节点就完事了,还要保证删除后还是一颗排序二叉树。
删除节点有四种情况:
- 删除的结点左右子树为空 ,如 3
- 删除的结点左子树不空,右子树为空 ,如37
- 删除的结点左子树为空 ,右子树不空,如 61
- 删除的结点左右子树都不空,如 12
对于第一种情况:删除3
直接释放 该节点就行。
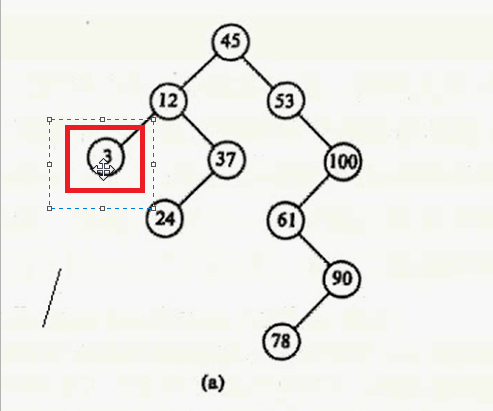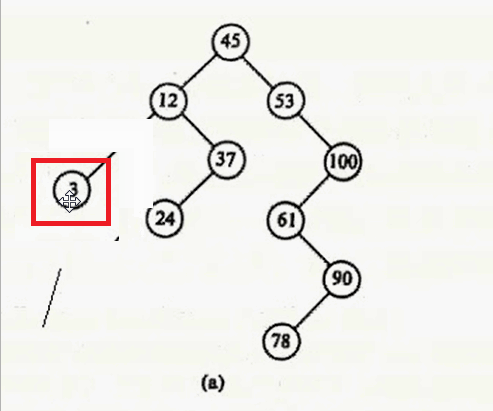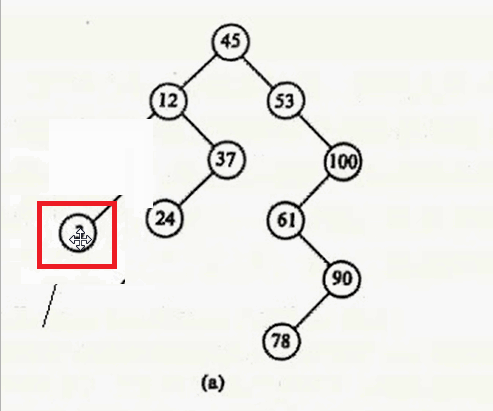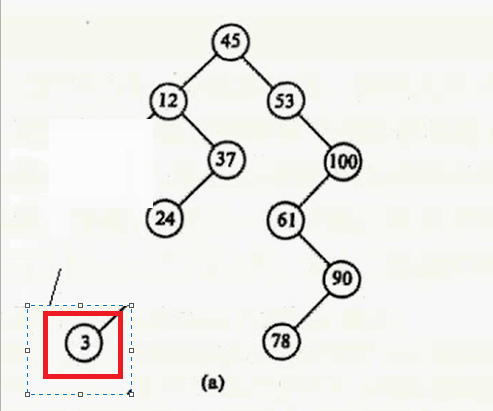
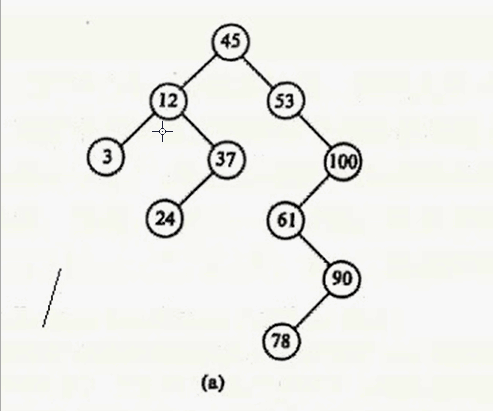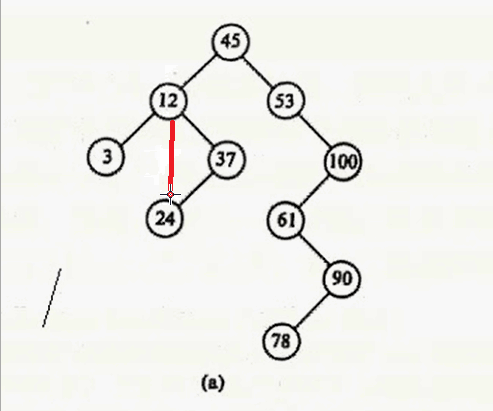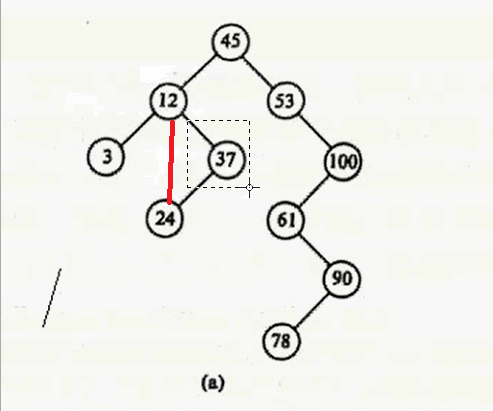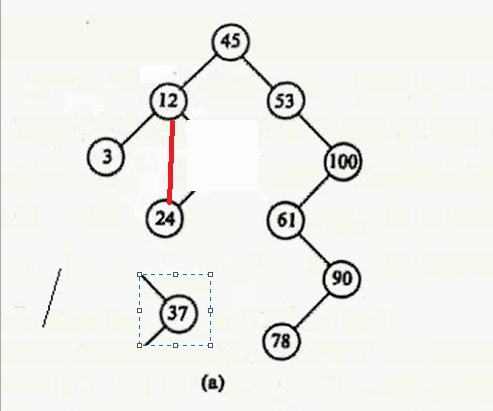
对于第二种情况:删除37
让 12 的右子树 指向 37 的左子树就可以啦。
那 12 的右子树是什么呢?
就是 37的结点指针咯,也就是要删除的结点咯,在我们的代码也就是 *node咯。
37的左子树是什么?
就是 node->lChild 咯。
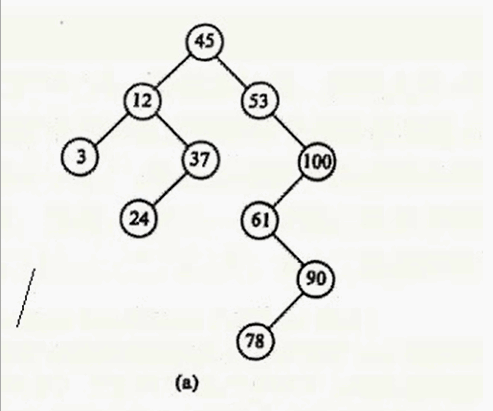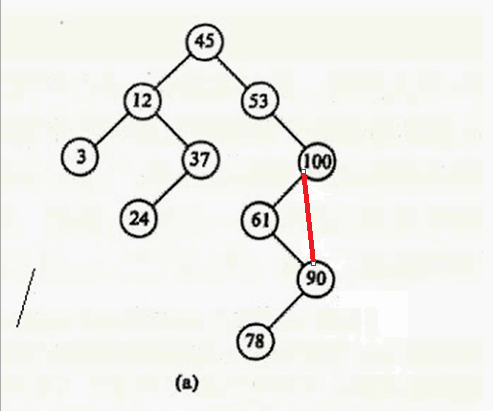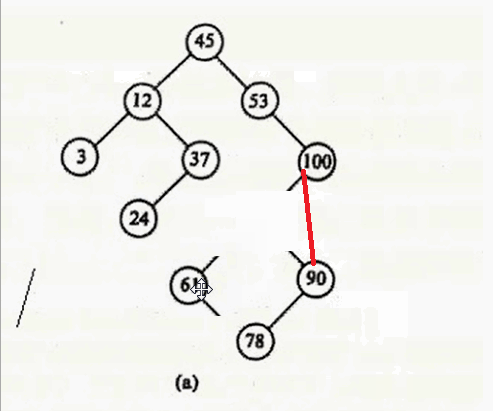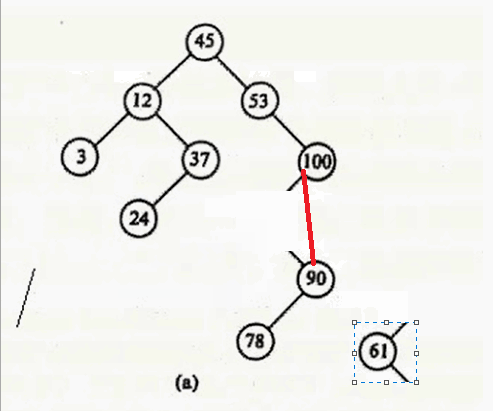
对于第三种情况:删除61
让 100的左子树指向61的右子树就可以啦。
那 100的左子树是谁?
就是你要删除的结点node咯。
那 61的右子树是谁?
就是 *node->rChlid咯;
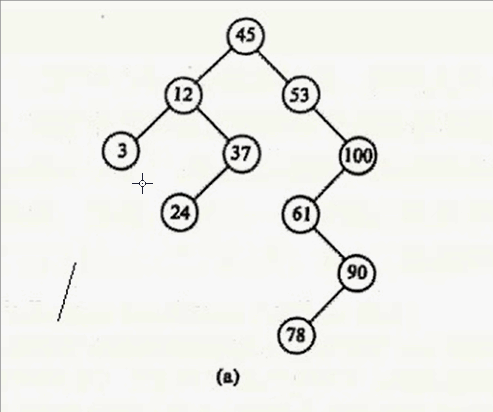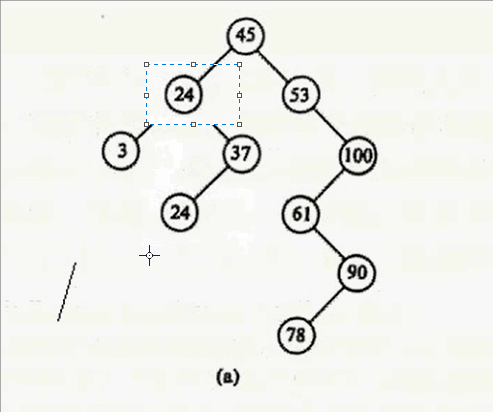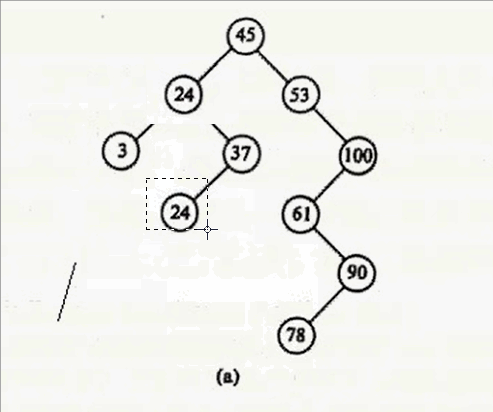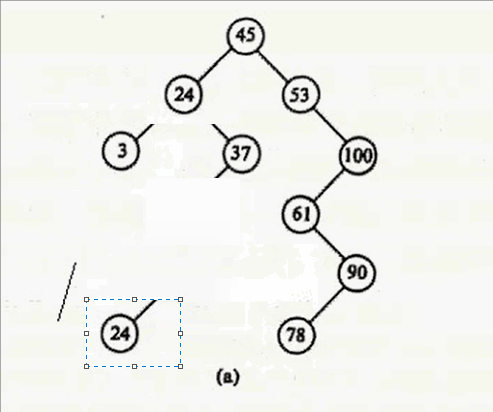
最后一种情况:删除12
其实只要在要删除结点的右子树中找到其最小值,用这个最小值覆盖要删除的结点就行,然后把最小值删除掉。什么意思呢?要删除12,就在12 的右子树找到最小值24,用24 覆盖 12,则12的数据就变成24,然后删除24。
好了,四种情况说完,给你们上代码:
bool Remove(BSTree* bt, ElementType key)
{
return Remove(&bt->root, key);
}
bool Remove(BSTreeNode** node, ElementType key)
{
if (*node == NULL) //空树不删
return 0;
if (key < (*node)->date) //去左子树找key删
Remove(&(*node)->lChild, key);
else if (key > (*node)->date) //去右子树找key删
Remove(&(*node)->rChild, key);
//若key找到就删除 即 key == date;
//由于删除要保证还是一颗二叉树,所以有四种情况:
else
{
//删除的节点 左右子树为空,如本例的3
if ((*node)->lChild == NULL && (*node)->rChild == NULL)
{
free(*node);
*node = NULL;
}
//删除的节点 左子树不为空,右子树为空 如本例的37
else if ((*node)->lChild != NULL && (*node)->rChild == NULL)
{
BSTreeNode* cur = *node; //定义个临时变量cur指向要删除的节点
//开始删除
*node = (*node)->lChild;
free(cur);
}
else if ((*node)->lChild == NULL && (*node)->rChild != NULL)
{
BSTreeNode* cur = *node; //定义个临时变量cur指向要删除的节点
*node = (*node)->rChild;
free(cur);
}
//左右子树都不为空的情况
else
{
BSTreeNode* cur = (*node)->rChild;//cur指向要删除结点的右子树
//变量找到要删除结点右子树的最小的结点
while (cur->lChild != NULL)
cur = cur->lChild;
//退出循环后,要删除结点的右子树的最小值覆盖要删除的结点
(*node)->date = cur->date;
//删除右子树最小值的结点
Remove(&(*node)->rChild, cur->date);
}
}
}
好咯,二叉排序树就到这里结束咯,我们接下来看一种有意思的树,二叉平衡树,也是AVL树。
四 平衡二叉树(AVL)
0)AVL树相关的基本概念
先不说什么是平衡二叉树吧。我们来谈一谈上一个主题:二叉排序树。
二叉排序树的查找次数是不会超过树的深度的,但是同样的数据,会形成不同的二叉排序树。比如下图:
对于图(a),假如我要查找93,我只要比较3次就可以;对于图(b),我却要比较6次。明明都是二叉排序树,就因为树的形态不一样,就导致查找的效率会发生很大的变化。
所以我们在对此(b)的情况进行改进,使得它能够像(a)图那样,所以我们引入了平衡二叉树的概念。
什么是平衡二叉树呢?
左右子树的深度(高度)之差的绝对值不能超过1的树叫做平衡二叉树。平衡二叉树是在二叉排序树的基础上过来的,本质还是二叉排序树,只是平衡二叉树是二叉排序树的一种特殊情况。
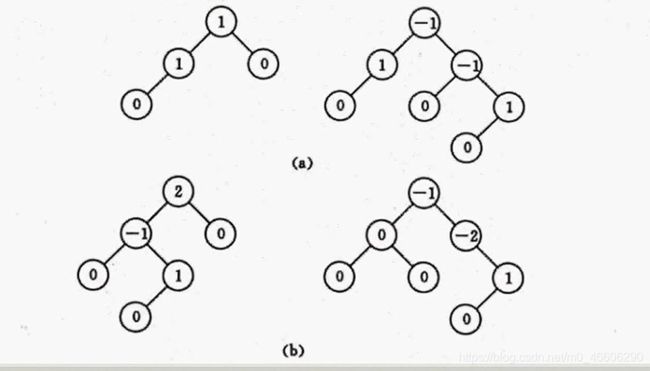
什么是平衡因子?
我们把某节点的右子树的深度减去左子树的深度的值叫做平衡因子(左减右也行,只是我们习惯右减左),平衡因子的值只有 0 -1 1;
看看图理解下(这是左减右),我在《数据结构》严蔚敏结的图。关注的是某个结点哦。
如何调整平衡?
我们认为,只要平衡因子的绝对值大于1就不平衡,这时候我们需要调整平衡。
在树的插入和删除操作才会破坏树的平衡,所以我们主要在这两个操作上调整平衡。
假如在我们插入一组数据:13 24 37 90 53

在插入到37的时候13的平衡因子变成2了,所以我们就要调整二叉树。
调整的方式有四种:
- 单旋转:
- 左旋转
- 右旋转
- 双旋转:
- 先左后右旋转
- 先右后左旋转
什么时候进行这几种旋转呢?
对于单旋转,只要三个结点在同一条线上就行,那进行左单旋转和右单旋转又怎么分?只要看不平衡的因子那颗结点的左树低于右数就左旋转,右数低于左树就右旋转,就是哪边树低就旋转过去哪边。
例如:
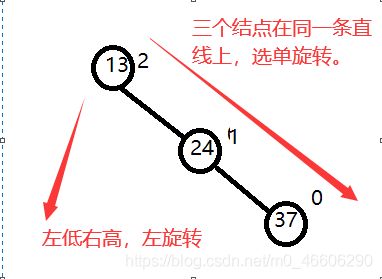
旋转过程: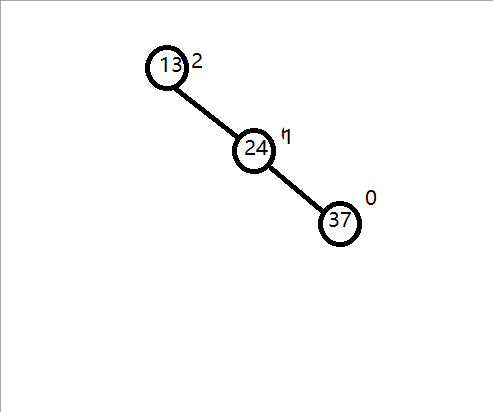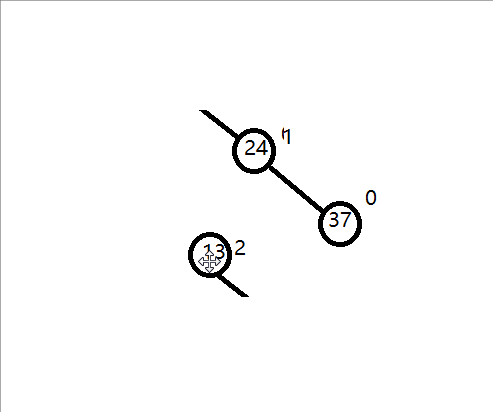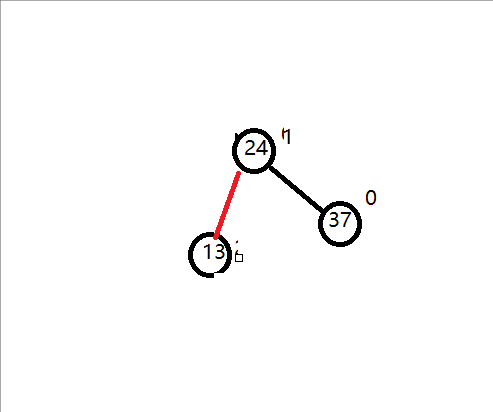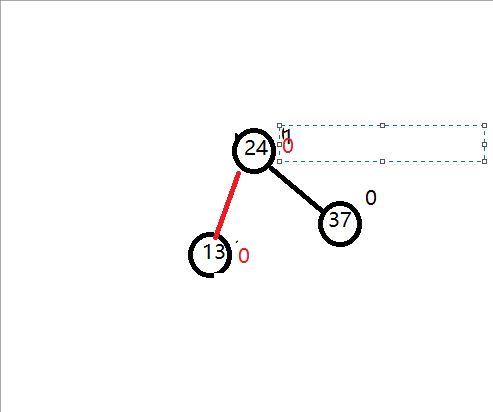
最终变成:所有节点的平衡因子都绝对值都是小于1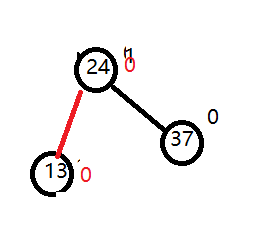
右旋转可以自己找个例子试一试:如:30 20 10.我就不演示了。

接下来看看什么时候双旋转?
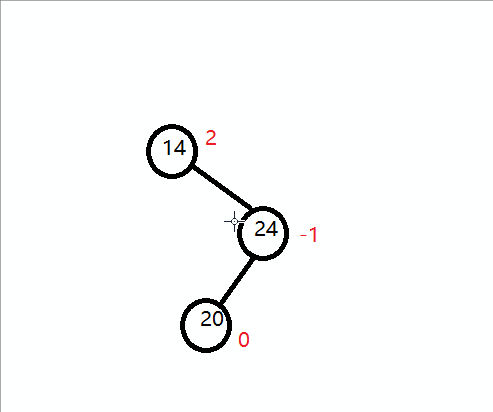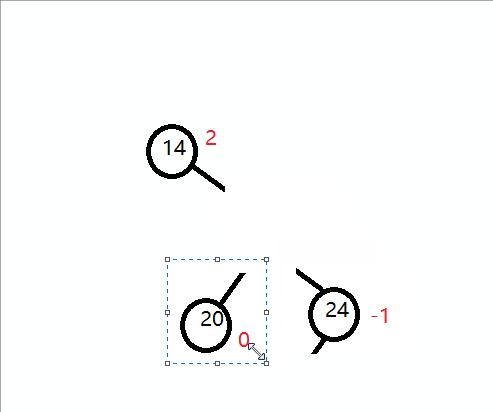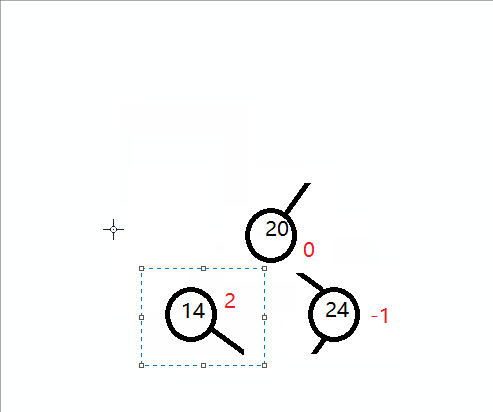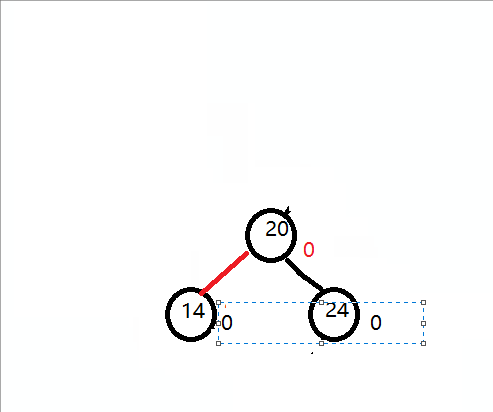
插入一组数据:14 24 20 .如下图:
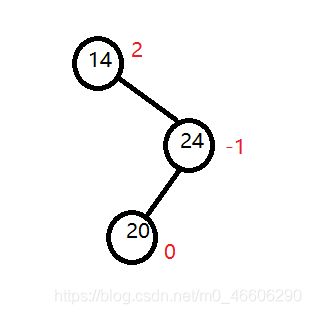
三个结点不是形成一条直线,而是折线。我把它记为:右箭头形式,然后右箭头先,就先进行先右后左的旋转,那如何旋转呢?
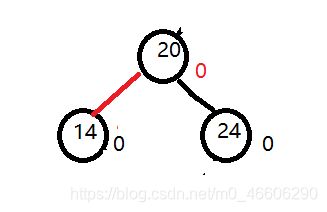
观察以下图:14的平衡因子是2,24的平衡因子是 -1,这两个平衡因子符号不统一,而对于我们的单旋转,无论是左旋转还是右旋转,他们平衡因子都是符号统一的。所以我们顺着这思路,我们先把符号统一先,同一标准是把符号统一到和不平衡的结点的平衡因子符号相同就行,即对于上图,把24 右旋转先就可以。然后我们就可以再对14左旋转。
如下示意图:
对于先左后右的旋转思路和上面一致,给你一组数据:30 20 25.
你自己演示以下哦。
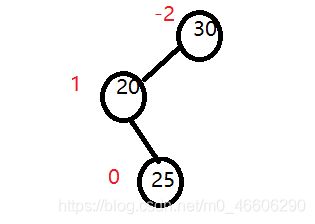
无论你是单旋转还是双旋转,最终都是保持一个特性:二叉排序树的模样。
1)平衡二叉树的存储结构
也就是比二叉树多了个平衡因子。没区别的哦。
#define EleTyp int
//结点类型
typedef struct AVLNode
{
EleTyp date; //数据域
struct AVLNode* lChild;
struct AVLNode* rChild;
int bf; //平衡因子
}AVLNode;
//树类型
typedef struct AVLTree
{ //指向树根;
struct AVLNode* root;
}AVLTree;
2)初始化平衡二叉树
就初始化根即可。
void InitAVl(AVLTree* bt)
{
bt->root = NULL;
}
3)平衡二叉树的插入
1.插入
bool InsertAVl(AVLTree* bt, EleTyp x)
{
return InsertAVl_(bt->root, x);
}
bool InsertAVl_(AVLNode*& node, EleTyp x)
{
if (node == NULL) //插入根节点
{
node = (AVLNode*)malloc(sizeof(AVLNode));
node->date = x;
node->lChild = NULL;
node->rChild = NULL;
node->bf = 0;
return 1; //插入成功
}
AVLNode* cur = node; //定义cur指向根结点,方便迭代移动
AVLNode* parent = NULL; //定义父结点,用于链接两个结点,和回溯修改平衡因子
SeqStack st;
InitStack(&st);
//给x寻找插入的位置
while (cur != NULL)
{
if (x == cur->date)
return 0; //插入失败
parent = cur; //,cur移动前记录cur的父结点
PushStack(&st, parent); //把cur父结点入栈,为了回溯调整平衡因子
if (x < cur->date)
cur = cur->lChild;
else
cur = cur->rChild;
}//退出循环后,插入结点
cur = (AVLNode*)malloc(sizeof(AVLNode));
cur->date = x;
cur->lChild = NULL;
cur->rChild = NULL;
cur->bf = 0;
//插入结点后,要链接成树的模样
if (x < parent->date) //插入的值x小于cur的父结点,就链接左
parent->lChild = cur;
else//插入的值x大于于cur的父结点,就链接右
parent->rChild = cur;
/
//调整平衡因子bf,就是出栈回溯到parent处调整
while (!IsEmpty(&st))
{ //回溯
parent = GetStackTop(&st);
PopStack(&st);
//调整
if (parent->lChild == cur) //cur插入的是parent的左树,父结点平衡因子减一
parent->bf--;
else //cur插入的是parent的右树,父结点平衡因子加一
parent->bf++;
//调整后,父节点的平衡因子为0,则调整平衡
if (parent->bf == 0)
break;
//调整后,若父结点平衡因子为 1 或-1,则继续回溯调整
if (parent->bf == 1 || parent->bf == -1)
cur = parent; //cur回溯上一结点
else //平衡因子不是 1 -1 ,0,则旋转化调整。
{ //定义一个标志结点
int flag = (parent->bf < 0) ? -1 : 1;
//cur结点的bf符号与parent的bf同号,在同一直接,单旋转
if (cur->bf == flag) //cur的bf只有 1,-1
{
//右旋转
if (flag == -1)
RotateR(parent);
else //左旋转
RotateL(parent);
}
else//cur结点的bf符号与parent的bf异号,双旋转
{
if (flag == -1)
RotateLR(parent);
else
RotateRL(parent);
}
break;
}
}//调整结束后,连接调整后的树
if (!IsEmpty(&st))
node = parent;
else
{
AVLNode* cur = GetStackTop(&st);
if (cur->date > parent->date)
cur->lChild = parent;
else
cur->rChild = parent;
}
return 1;
}
总结以下步骤:
- 先插入根结点
- 寻找x的插入位置,找到插入
- 插入后链接结点
- 调节平衡因子
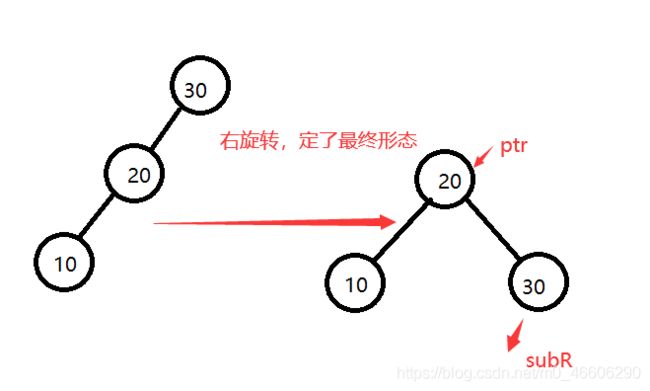
2.右旋转
对于单旋转最重要的就是知道旋转最后的形态,然后,把指针指向定下来就可以咯。
如下图:
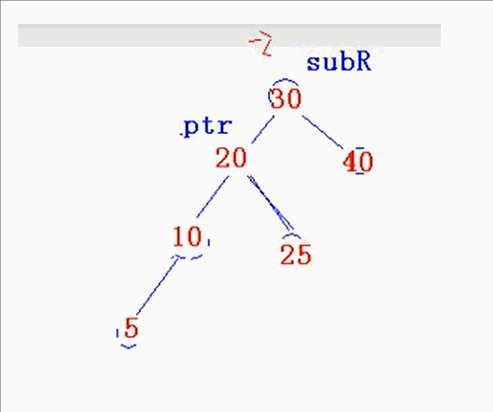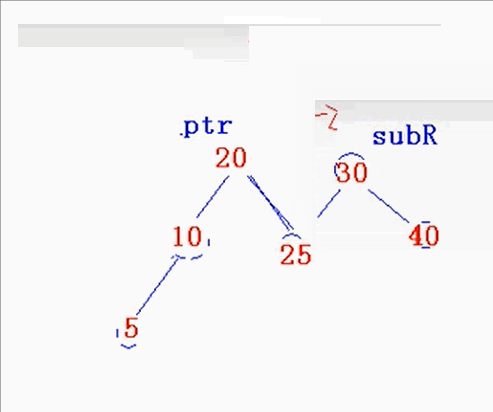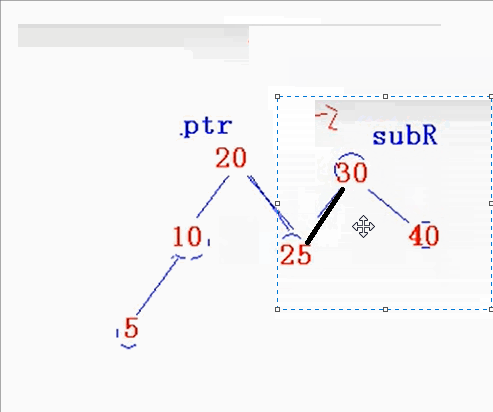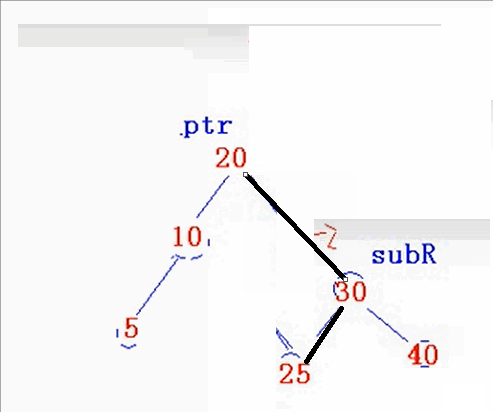
void RotateR(AVLNode*& ptr)
{
//调整平衡
AVLNode* subR = ptr;
ptr = subR->lChild;
subR->lChild = ptr->rChild;
ptr->rChild = subR;
//调整bf
ptr->bf = 0;
subR->bf = 0;
}
思路:如何想的算法呢?
-
首先由于是右旋转,那就是右低左高,先得知树得最终形态,把prt和sub指针确定下来,
-
然后再考虑旋转subR过程中prt的右树是否有结点,有的话就插入subR的左子树,
-
为什么是subR左子树,因为你最终能的形态已经确定了,所以只能插入subR的左子树。
3.左旋转
和右旋转对称
void RotateL(AVLNode*& ptr)
{
AVLNode* subL = ptr;
ptr = subL->rChild;
subL->rChild = ptr->lChild;
ptr->lChild = subL;
ptr->bf = 0;
subL = 0;
}
4.先左后右旋转
void PotateLR(AVLNode*& ptr)
{
AVLNode* subR = ptr;
AVLNode* subL = subR->lChild;
ptr = subL->rChild;
//ptr 有左树的情况
subL->rChild = ptr->lChild;
ptr->lChild = subL;
//调整subL 的bf
if (ptr->bf <= 0) //即ptr有左树
subL->bf = 0;
else
subL->bf = -1; //subL必定有左树
//ptr有右树的情况
subR->lChild = ptr->rChild;
ptr->rChild = subR;
if (ptr->bf == -1) //ptr无右树
subR->bf = 1; //subR必定有右树
else
subR->bf = 0;
ptr->bf = 0; //ptr最终平衡因子为0
}
5.先右后左旋转
void RotateRL(AVLNode*& ptr)
{
AVLNode* subL = ptr;
AVLNode* subR = subL->rChild;
ptr = subR->lChild;
subR->lChild = ptr->rChild;
ptr->rChild = subR;
if (ptr->bf >= 0) //ptr无左树
subR->bf = 0;
else
subR->bf = 1;
subL->rChild = ptr->lChild;
ptr->lChild = subL;
if (ptr->bf == 1) //ptr有右树
subL->bf = -1;
else
subL->bf = 0;
ptr->bf = 0; //最终ptr 的 bf = 0
}
寄语
二叉树的操作不止这么一点,我只是分享了比较常规和重要的一些操作。希望能给你们一些引发,保持继续学习的动力。