数据结构与算法--二叉树之线索二叉树(前序、中序、后序)思路以及代码实现。
线索二叉树
-
- 1.先序线索二叉树
- 2.后序线索二叉树
- 3.中序线索二叉树
- 4.代码打印结果:
1.先序线索二叉树
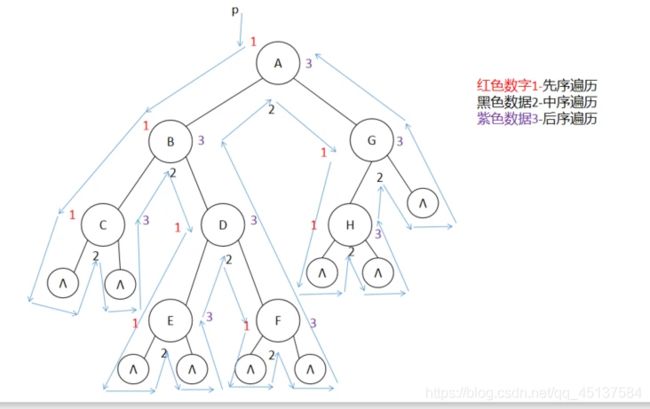
思路:
沿类似于上图中的先序遍历路径行走,如果发现左孩子结点或右孩子结点为空(也就是度为1或者0的结点),把它们的左空孩子结点指向它的前驱结点,把它们的右空孩子结点指向它的后继结点。当没有前驱或者后继结点时不用指。
关于如何找到它们的前驱或后继结点?
如下图:
我们可以通过图中(+)加号的看出路径,可以得到先序遍历的顺序为:
1 2 4 5 3 6 8 7
我们以图中结点4为例子:
4为叶子结点,所以它的左右孩子结点都为空结点,我们可以从先序遍历的顺序看出,4的前驱结点为2,4的后继结点为5,其他同理可得,所以得到如图的连线。

我们把上图用代码表示出来,我们使用链式存储结构,让上图可视化:

由五个域组成
lichild:用来存储左孩子所在的链结点存储地址。
lTag:当ITag为0表示左孩子结点不空;为1表示空。
rchild:用来存储右孩子所在的链结点存储地址。
rTag:当rTag为1表示右孩子结点不空;为1表示空。
data:用来存储数据。

和我们使用的是先序遍历的递归很像。顺序为:
根结点->左子树->右子树
代码如下:
void _preThread(BTNode<T> *p,BTNode<T> *&pre)
{
if(p!=NULL)
{
//当遇到左结点为NULL时,把左孩子结点指向前驱结点;把lTag设为1,表示左孩子结点为空
if(p->lchild==NULL)
{
p->lchild=pre;
p->lTag=1;
}
//当遇到结点不为空且右孩子结点为NULL时,把右孩子结点指向后继结点;把rTag设为1,表示右孩子结点为空
if(pre!=NULL&&pre->rchild==NULL)
{
pre->rchild=p;
pre->rTag=1;
}
//根结点
pre=p;
//左子树
if(p->lTag==0)
_preThread(p->lchild,pre);
//右子树
if(p->rTag==0)
_preThread(p->rchild,pre);
}
}
虽然我们实现了先序线索二叉树 ,但是要使用它来遍历打印出数据。
思路:
首先指向根结点,然后根结点的,左子结点,左子结点的左子结点…不为空的话,就沿路打印出所到结点;然后当左结点为空时,指向它的右子结点(部分右子结点是他的后继结点);然后继续判断左结点是否为空,这样循环就可以打印出我们想要的数据了。
打印路径:如图红色线条
因为我们没有用前驱结点,我就把它删掉了。后面的后序遍历我们就只使用前驱结点,没使用后继结点。
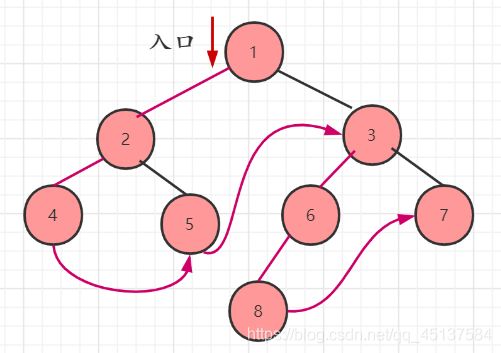
代码表示:
//线索二叉树前序遍历
void preThread()
{
BTNode<T> *p=NULL;
BTNode<T> *root=_root;
_preThread(root,p);
while(root!=NULL)
{
while(!root->lTag)
{
cout<<root->data<<" ";
root=root->lchild;
}
cout<<root->data<<" ";
root=root->rchild;
}
cout<<endl;
}
整体代码:
#include2.后序线索二叉树
因为和前序二叉树有点像,所以就先说明后序线索二叉树。

思路:
沿类似于上图中的后序遍历路径行走,如果发现左孩子结点或右孩子结点为空(也就是度为1或者0的结点),把它们的左空孩子结点指向它的前驱结点,把它们的右空孩子结点指向它的后继结点。当没有前驱或者后继结点时不用指。
关于如何找到它们的前驱或后继结点?
如下图:
我们可以通过图中(-)负号的看出路径,可以得到后序遍历的顺序为:
4 5 2 8 6 7 3 1
我们以图中结点4为例子:
4为叶子结点,所以它的左右孩子结点都为空结点,我们可以从后序遍历的顺序看出,4的没有前驱结点,4的后继结点为5,其他同理可得,所以得到如图的连线。
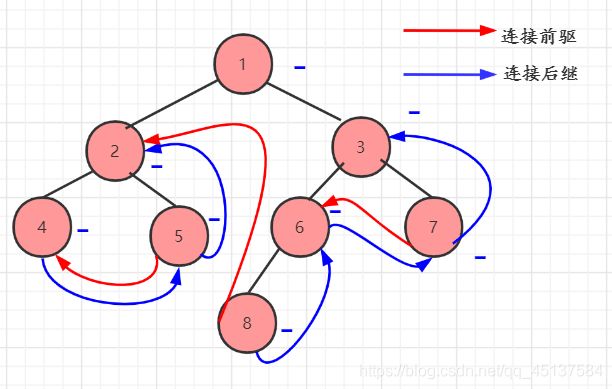
我们把上图用代码表示出来,我们使用链式存储结构,让上图可视化:

由五个域组成
lichild:用来存储左孩子所在的链结点存储地址。
lTag:当ITag为0表示左孩子结点不空;为1表示空。
rchild:用来存储右孩子所在的链结点存储地址。
rTag:当rTag为1表示右孩子结点不空;为1表示空。
data:用来存储数据。
和我们前面的先序线索二叉树非常类似,只是代码的顺序不同,因为这个是左子树->右子树->根结点
代码如下:
void _postThread(BTNode<T> *p,BTNode<T> *&pre)
{
if(p!=NULL)
{
//左子树
_postThread(p->lchild,pre);
//右子树
_postThread(p->rchild,pre);
//当遇到左结点为NULL时,把左孩子结点指向前驱结点;把lTag设为1,表示左孩子结点为空
if(p->lchild==NULL)
{
p->lchild=pre;
p->lTag=1;
}
//当遇到结点不为空且右孩子结点为NULL时,把右孩子结点指向后继结点;把rTag设为1,表示右孩子结点为空
if(pre!=NULL&&pre->rchild==NULL)
{
pre->rchild=p;
pre->rTag=1;
}
//根结点
pre=p;
}
}
虽然我们实现了后序线索二叉树 ,但是要使用它来遍历打印出数据。
思路:
因为我们和先序遍历一样的方向,难以达到我们想要的效果,如果我们从与它相反的路径来看的话,我们所想要解决问题是不是就很明确,和我们先序遍历的解决方法和类似,不过打印出的数据是逆后序遍历,所以我们需要一个自定义栈来存储逆后序遍历,出栈则为后序遍历。
打印路径:如图红色线条
因为我们没有用后继驱结点,我就把它删掉了。
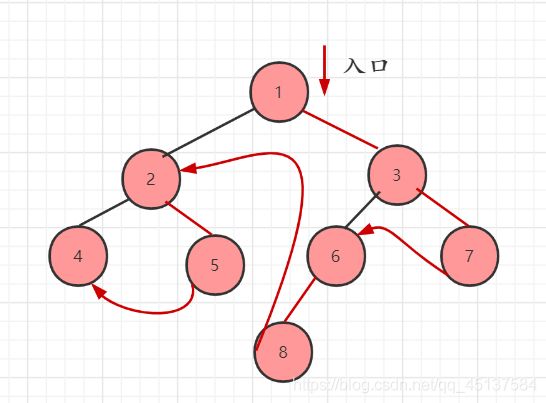
代码表示:
void postThread()
{
BTNode<T> *p=NULL;
BTNode<T> *root2=_root;
BTNode<T> *stack[maxSize];
int top=-1;
_postThread(root2,p);
while(root2!=NULL)
{
while(!root2->rTag)
{
stack[++top]=root2;
root2=root2->rchild;
}
stack[++top]=root2;
root2=root2->lchild;
}
while(top!=-1)
{
p=stack[top--];
cout<<p->data<<" ";
}
cout<<endl;
}
整体代码:
#include3.中序线索二叉树

思路:
沿类似于上图中的中序遍历路径行走,如果发现左孩子结点或右孩子结点为空(也就是度为1或者0的结点),把它们的左空孩子结点指向它的前驱结点,把它们的右空孩子结点指向它的后继结点。当没有前驱或者后继结点时不用指。
关于如何找到它们的前驱或后继结点?
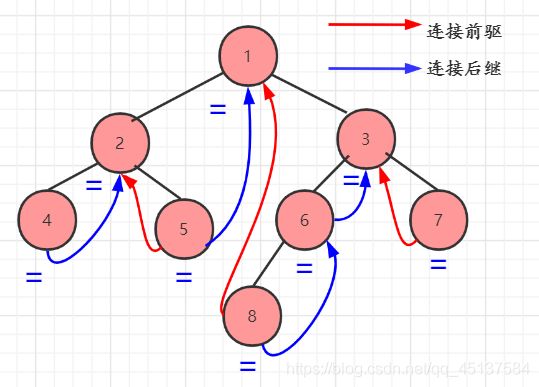
如下图:
我们可以通过图中(=)等于号的看出路径,可以得到中序遍历的顺序为:
4 2 5 1 8 6 3 7
我们以图中结点4为例子:
4为叶子结点,所以它的左右孩子结点都为空结点,我们可以从后序遍历的顺序看出,4的没有前驱结点,4的后继结点为2,其他同理可得,所以得到如图的连线。
我们把上图用代码表示出来,我们使用链式存储结构,让上图可视化:

由五个域组成
lichild:用来存储左孩子所在的链结点存储地址。
lTag:当ITag为0表示左孩子结点不空;为1表示空。
rchild:用来存储右孩子所在的链结点存储地址。
rTag:当rTag为1表示右孩子结点不空;为1表示空。
data:用来存储数据。
和我们中序遍历的递归非常类似,顺序为:
左子树->根结点->右子树
代码:
void _inThread(BTNode<T> *&p,BTNode<T> *&pre)
{
if(p!=NULL)
{
//左子树
_inThread(p->lchild,pre);
//当遇到左结点为NULL时,把左孩子结点指向前驱结点;把lTag设为1,表示左孩子结点为空
if(p->lchild==NULL)
{
p->lchild=pre;
p->lTag=1;
}
//当遇到结点不为空且右孩子结点为NULL时,把右孩子结点指向后继结点;把rTag设为1,表示右孩子结点为空
if(pre!=NULL&&pre->rchild==NULL)
{
pre->rchild=p;
pre->rTag=1;
}
//根结点
pre=p;
//右子树
_inThread(p->rchild,pre);
}
}
虽然我们实现了中序线索二叉树 ,但是要使用它来遍历打印出数据。
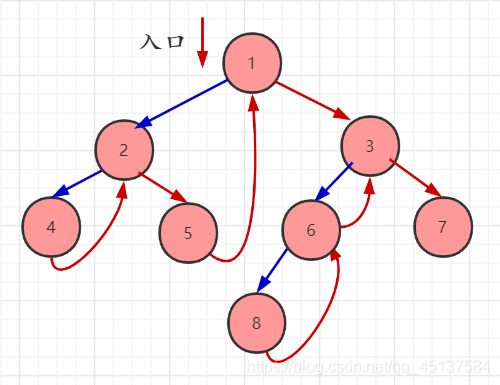
图中:
蓝色箭头+红色箭头为路径,其中红色箭头的起点为打印结点。
思路:
沿如图入口处进入,如果遇到存在结点且左子结点不空,使用它的左子结点等于当前结点,当结点的左子结点为空时,我们打印出当前结点;然后判断右子结点是否为空,当为空时,使结点的后继结点等于当前结点,当不为空时,使结点的右子结点等于当前结点,然后继续 判断当前结点存在结点且左子结点不空,让左子结点等于当前结点;然后循环进行。
看代码可能更轻易看懂:
void inThread()
{
BTNode<T> *p=NULL;
BTNode<T> *root1=_root;
_inThread(root1,p);
while(root1!=NULL&&root1->lTag==0)
{
root1=root1->lchild;
}
while(root1!=NULL)
{
cout<<root1->data<<" ";
if(root1->rTag==1){
root1=root1->rchild;
}else{
root1=root1->rchild;
while(root1!=NULL&&root1->lTag==0)
{
root1=root1->lchild;
}
}
}
cout<<endl;
}
整体代码:
#include