CSAPP lab1 data lab

记录，会有错的地方

bitXor

异或的表达式是

题目要求是只要~和&,尝试过用德摩根率

但是这样太麻烦了，这里我是用同或取反得到的

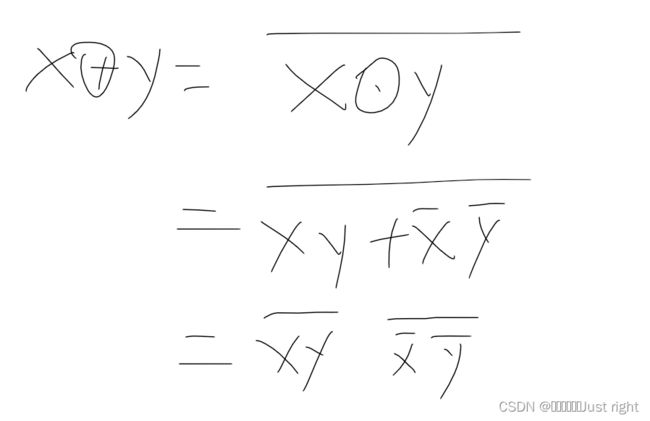
int bitXor(int x,int y){
	return ~(~x&~y)&(~x&y);
}

tmin

要求返回int类型的最小值,int是有符号数，有符号数的最小值就是最高位为1，其余位为0，让1<<31位即可得到

int tmin(void)
{
	return 1<<31;
}

isTmax

判断x是否是Tmax，若是返回1，反之0，首先构造出Tmax,Tmax与Tmin的联系
Tmin就是最高位是1，其余是0，Tmax是最高位是0，其余是1，也就是说Tmax = ~Tmin

tips

判断是否是一个数的时候，用异或比较好

int isTmax(int x){
	//若是Tmax，异或得到的结果是0，要取反
	return !(x^(~(1<<31));
}

allOddBits

如果一个数奇数位为1返回1
第一步:把这个数构造出来,题目有限制，只能用一个字节的，但是我们可以通过移位的方式来构造
第二部:把给出的x与我们构造的数相与，再和我们构造的进行异或，就是看x是否是等于我们构造的数，注意，最后结果需要取反

int allOddBits(int x){
	int mask = 0xaa;
	mask = mask + (temp<<8) +(mask<<16)+(mask<<24);
	return !((x & mask)^mask);
}

negate

我看其他人说是求相反数,我只是写一下这个算的过程
这里以2为例子
0000 0000 0000 0000 0000 0000 0000 0010
~2
1111 1111 1111 1111 1111 1111 1111 1101 (补码,所以要再求补)
1000 0000 0000 0000 0000 0000 0000 0010（反码）
1000 0000 0000 0000 0000 0000 0000 0011(补码)
所以~2=-3,加1得到-2
来点推导
无论哪个数
x+~x=-1 -> x + ~x +1 =0 -> ~x + 1=-x

int negate(int x){
	return ~x+1;
}

isAsciiDigit

判断给定的int值是否在’0’和’9’之间,就是实现一个不等式
48<=x<=57,拆成两个式子

1. 48<=x => x-48>=0
2. x<=57 => 57 -x>=0
   -x = ~x+1，如果x不在这个区间里面那么必定有一个式子的值是小于0的，也就是他的符号位是1

	int a=x+(~(0x30)+1);
	int b=(~x+1)+0x39;
	int c=a>>31;
	int d=b>>31;
	return !c&!d;

conditional

实现一个x?y:z
我们想要达到的目的是构造一个mask使得当
x=0 mask & x =0 且 mask & z =z
x!=0 mask & x= x且 mask & z=0
这里解释一下代码中的!!x,!是C语言的取反运算符，得到的结果只有1和0，非0取反为1，0取反为1
当x=0的时候
!!x=0,0<<31 =0,再右移依然等于0
当x!=0的时候，!!x=1
1<<31 = Tmin ,Tmin>>31=-1,~-1=0,
为什么~-1=0
-1 在计算机中表示是
1111 11111 1111 11111 1111 11111 1111 11111(补码)
进行取反
0000 0000 0000 0000 0000 0000 0000 0000(符号位是0，那么这个就是真值了，就是0了)

int conditional(int x,int y,int z){
	x = ((!!x)<<31)>>31;
	return (~x & z) | (x & y);
	
}

isLessOrEqual

当x<=y返回1,x>y 返回0
这里分两种情况

1. 异号，只要x是负数,y是整数返回1即可
2. 同好,若y-x>=0就返回1
   y-x在代码中反应出来就是 y+(~x+1)

int isLessOrEqual(int x,int y){
	int signX = (x>>31) & 1;//这里改成(x>>31)^0也是可以的
	int signY = (y>>31) & 1;
	int different = signX ^ signY;//若x,y为异号就是1，反之为0
	int special = different & signX; // 这个是判断第一种情况的，就是x为负数(signX=1)，y为正数(signY=0)
	// 若y>=x 那么y-x>=0 那么符号位是0，!0=1 1&1=1
	int sign = !isEqual & !((y+~x+1)>>31) & 1;
	return special | sign;
}

logicalNeg

实现运算符!
当x =0 返回1,这一步特别好搞,直接+1
当x!=0 返回0,若是按照上面的做法就是当x!=0，我们想办法让他=-1并且不能影响x=0的情况,再直接加一
这里有一个小技巧,让x与-x进行异或再右移31位，这样非0的数最后得到的结果恒等于-1，x与-x的符号位是相反的，最高位必然是1，那么再进行右移操作的时候会被移动成-1，因为这里的右移是算数右移

int logicalNeg(int x){

	int cmp = (x^(~x+1))>>31;//非0的数这一步的结果恒等于-1，若为0，那么cmp=0;
	return cmp +1;
}

howManyBits

计算一个int类型需要多少位
提示:这里可能用的了二分的思想
若是正数需要找到最高位的1
若是负数需要找到最高位的0，为什么呢?因为在展开求和的过程中只有1是有效的，0无效

我们反着来试试，我们要找24这个数需要多少位来表示，我们找最高位的0出现的位置
11000,最高位0出现的位置是第3位,但是3位表示不了
-24呢?由于是用补码存储的，原先有很多0，我的意思如下所示
1000 0000 0000 0000 0000 0000 0001 1000(看到没有符号位后面有很多0，由于补码需要由原码取反+1得到，所以原先有很多0变成了1)
1111 1111 1111 1111 1111 1111 1110 0111
1111 1111 1111 1111 1111 1111 1110 1000
这里我们统一转换成正数，若是负数转换成正数

int howManyBits(int x){
	int sign = x>>31;//取得符号位 <0则为1 >0则为0
	int res = 0;
	//为0不用管，为1 需要对x进行取反
	int tmp = (sign & ~x) | (~sign &x);
	x = tmp;//更新x的值
	//先右移15位若不为0，那么!!(tmp>>15)恒等于1,1<<4就是16;若右移15位为0,那么!!(tmp>>15)恒等于0，0<<4=0
	res = !!(tmp>>15)<<4;
	//在这种情况下 >> 等同于除法(向下取整) x / 2 ^res 
	tmp = x >> res;
	// 注意这里有个优先级的问题 式子展开:res = res | !!(tmp>>7)<<3,先算括号里面的,|的优先级大于<<
	// 在这里，按位或也就是|是等同于加法的(因为没有进位)
	// 假设tmp>>7不等于0 那么 就是 1<<3 = 8 
	// 16 | 8 
	/*
		1 0000  (16的二进制)
	  | 0 1000
	  = 1 1000 (24的二进制)
	下面就是一样的
	*/ 
	res |= !!(tmp>>7)<<3;//1
	tmp = x>>res;
	res |= !!(tmp>>3)<<2;//2
	tmp = x>>res;
	res |= !!(tmp>>1)<<1;//3
	tmp = x>>res;
	//看各个位是不是1,我们假设这个数是5哈, 那么标号为3的res是等于2的，tmp=5>>2=1
	res|=!!tmp;
	//要算符号位
	return res+1;
}

floatScale2

实现乘以2
首先来看一下IEEE 754标准(float)


思路:

1. 取得 s(阶符),exp,frac
2. 判定NaN,非规格化的
3. 处理规格化的

unsigned floatScale2(unsigned uf){
	unsigned s = (uf>>31)&1;
	unsigned expr = (uf>>23)&0xff;
	unsigned frac =uf & 0x7FFFFF;
	if(expr ==0 && frac ==0)
		return 0;
	//NaN
	if(expr == 0xff)
			return uf;
	//非规格化的 denormalize
	if(expr ==0)
	{	frac<<=1;
		//前面提到了，在没有进位的情况下，按位或就可以实现加法
		return (s<<31) | frac;
	}
	//规格化的 normalize
	expr++;
	return (s<<31) | (expr<<23) | frac;
}

floatFloat2Int

将一个浮点数转为整数

1. 取出s,expr,frac
2. 判定0,NaN
3. 处理正常情况

关于隐含的1

int floatFloat2Int(unsigned uf){
	unsigned s = (uf>>31)&1;
	unsigned expr = (uf>>23)&0xff;
	unsigned frac =uf & 0x7FFFFF;
	if(expr ===0 && frac==0)
		return 0;
	//判定为NaN
	if(expr ==0xff)
		return 1<<31;
	//判定为非规格化的
	if(expr==0)
	{
		//非规格化的数 127= 2^8-1 之所以是8是因为IEEE 标准中float expr占8位
		//e = 1-127=-126 都2^-126了，这个数字无限接近于0，哪怕尾数全为1，也是无限接近于0，这里直接返回0
		return 0;
	}
	//规格化的 e = expr - bias 并且 frac = 1 + frac
	int e = expr - 127;
	//先把 隐含的1加上 并且此时的frac已经是乘以2^23次方的结果，接下来就是要根据e来判断是否需要左移和右移
	// e>23 则左移，左移 (e-23)
	// e<23 则右移，右移 (23-e)
	frac = (1<<23) | frac;
	if(e>31)//e是31位，左移32位(才能进入到这个条件分支里面)就直接爆掉了
		return 1<<31;
	else if(e<0)
		// frac 是一个1.xxxxxx的小数，并且当e<0的时候等同于 (2 ^e)*1.xxxxxx =>1.xxxxx/2^e
		// 比如说1.000001/2 这个可以直接当成0
		return 0;
	if(e>=23)
		frac<<=(e-23);
	else
		frac>>=(23-e);
	if(s)
		//若是负数，返回其绝对值
		return ~frac+1;
	return frac;
		
	
}

floatPower2

对浮点数乘以2^x

unsigned floatPower2(int x) {
    if(x<-149)
            return 0;
    else if(x<-126)
    {
            int shift =  23+(x+126);
            return 1<<shift;
    }
    else if(x<=127){
        int expr = x+127;
        return expr<<23;
    }else
            return 0xFF<<23;

}