路径规划 | 蚁群算法图解与分析(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 从蚁群觅食说起
- 2 蚁群算法基本概念
- 3 蚁群算法流程
- 4 蚁群算法实现
-
- 4.1 ROS C++实现
- 4.2 Python实现
- 4.3 Matlab实现
0 专栏介绍
附C++/Python/Matlab全套代码课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 从蚁群觅食说起
蚁群算法(Ant Colony Optimization,ACO)的背景可以追溯到上世纪80年代末和90年代初。当时,Marco Dorigo和他的团队在研究分布式人工智能时,开始观察和研究蚂蚁的群体行为。他们发现,虽然单个蚂蚁的智能水平相对较低,但整个蚂蚁群体却能高效地完成复杂的任务,例如找到最短路径连接蚁巢和食物源。
在蚂蚁群体中,蚂蚁们会释放一种称为信息素的化学物质,用于与其他蚂蚁进行沟通。当蚂蚁发现食物后,它会沿着返回蚁巢的路径释放信息素。这些信息素在地面上留下了一条路径,并且越多的蚂蚁通过该路径,释放的信息素浓度就越高。高浓度的信息素会吸引更多的蚂蚁跟随该路径,形成一个正反馈的过程。然而,信息素也会随着时间的推移而逐渐挥发,导致路径的持续可塑性。
Marco Dorigo意识到这种自组织行为可能对解决实际问题的优化具有启示性。他在他的博士论文中将这种观察与一种迭代的优化算法相结合,用于解决组合优化问题,例如旅行商问题(TSP)和任务分配问题。这就是蚁群算法的诞生。
蚁群算法的基本思想是通过模拟蚂蚁在寻找最优路径时的行为,利用信息素和启发式信息来引导搜索过程,从而找到问题的最优解。蚁群算法在优化问题中表现出色,并且在路由优化、资源调度、图优化等领域有广泛的应用。它的独特之处在于其去中心化和自适应性,这使得它在处理复杂问题时表现出很好的鲁棒性和适应性。
2 蚁群算法基本概念
蚁群算法是一种启发式优化算法,其核心原理是通过蚂蚁在搜索路径上留下能够吸引其他蚂蚁的信息素,构造路径正反馈信息,经过一段时间演变后,从起始点到目的地最短路径上的信息素浓度强于其他路径,蚁群算法收敛。
蚁群算法的基本概念总结如下:
-
M M M:蚁群个体数量;
-
a l l o w e d k ( k = 1 , 2 , ⋯ , M ) \mathrm{allowed}_k\left( k=1,2,\cdots ,M \right) allowedk(k=1,2,⋯,M):蚂蚁 k k k的可行节点表,其中屏蔽了障碍与已访问节点;
-
t a b u k ( k = 1 , 2 , ⋯ , M ) \mathrm{tabu}_k\left( k=1,2,\cdots ,M \right) tabuk(k=1,2,⋯,M):蚂蚁 k k k的禁忌节点表,按顺序记录了蚂蚁 k k k的已访问节点;
-
τ i j \tau _{ij} τij:节点 i i i与节点 j j j间路径的信息素浓度,初始时刻 τ i j ( 0 ) = C \tau _{ij}\left( 0 \right) =C τij(0)=C, C C C为小数值正数。当蚂蚁种群完成一次迭代后,按
τ i j ∗ = ( 1 − ρ ) τ i j + Δ τ i j \tau _{ij}^{*}=\left( 1-\rho \right) \tau _{ij}+\varDelta \tau _{ij} τij∗=(1−ρ)τij+Δτij更新信息素浓度,其中 ρ ∈ ( 0 , 1 ) \rho \in \left( 0,1 \right) ρ∈(0,1)为信息素挥发系数, 1 − ρ 1-\rho 1−ρ则为信息素残留系数, Δ τ i j \varDelta \tau _{ij} Δτij为本次迭代在路径 ( i , j ) \left( i,j \right) (i,j)上的信息素增量,初始时刻 Δ τ i j ( 0 ) = 0 \varDelta \tau _{ij}\left( 0 \right) =0 Δτij(0)=0,其他时刻按
Δ τ i j = ∑ k = 1 M Δ τ i j k \varDelta \tau _{ij}=\sum_{k=1}^M{\varDelta \tau _{ij}^{k}} Δτij=k=1∑MΔτijk计算,其中 Δ τ i j k \varDelta \tau _{ij}^{k} Δτijk为蚂蚁 k k k在路径 ( i , j ) \left( i,j \right) (i,j)上的信息素增量
Δ τ i j k = { Q L k , 蚂蚁 k 经过路径 ( i , j ) 0 , 蚂蚁 k 未经过路径 ( i , j ) \varDelta \tau _{ij}^{k}=\begin{cases} \frac{Q}{L_k}, \text{蚂蚁}k\text{经过路径}\left( i,j \right) \,\,\\ 0 ,\text{蚂蚁}k\text{未经过路径}\left( i,j \right) \,\,\\\end{cases} Δτijk={LkQ,蚂蚁k经过路径(i,j)0,蚂蚁k未经过路径(i,j)Q Q Q为信息素强度, L k L_k Lk为蚂蚁 k k k在本次迭代中走过的路径长度(造成的耗散损失);
-
η i j \eta _{ij} ηij:从节点 i i i向节点 j j j转移的启发式强度,可选为 η i j = 1 / d i j \eta _{ij}={{1}/{d_{ij}}} ηij=1/dij,其中 d i j d_{ij} dij为节点 i i i与节点 j j j间的距离;
-
p i j k p_{ij}^{k} pijk:蚂蚁 k k k从节点 i i i向节点 j j j转移的概率
p i j k = { [ τ i j ] α [ η i j ] β ∑ s ∈ a l l o w e d k [ τ i s ] α [ η i s ] β , j ∈ a l l o w e d k 0 , j ∉ a l l o w e d k p_{ij}^{k}=\begin{cases} \frac{\left[ \tau _{ij} \right] ^{\alpha}\left[ \eta _{ij} \right] ^{\beta}}{\sum_{s\in \mathrm{allowed}_k}{\left[ \tau _{is} \right] ^{\alpha}\left[ \eta _{is} \right] ^{\beta}}}, j\in \mathrm{allowed}_k\\ 0 , j\notin \mathrm{allowed}_k\\\end{cases} pijk=⎩ ⎨ ⎧∑s∈allowedk[τis]α[ηis]β[τij]α[ηij]β,j∈allowedk0,j∈/allowedk其中 α \alpha α、 β \beta β分别为信息素和启发式因子权重系数。
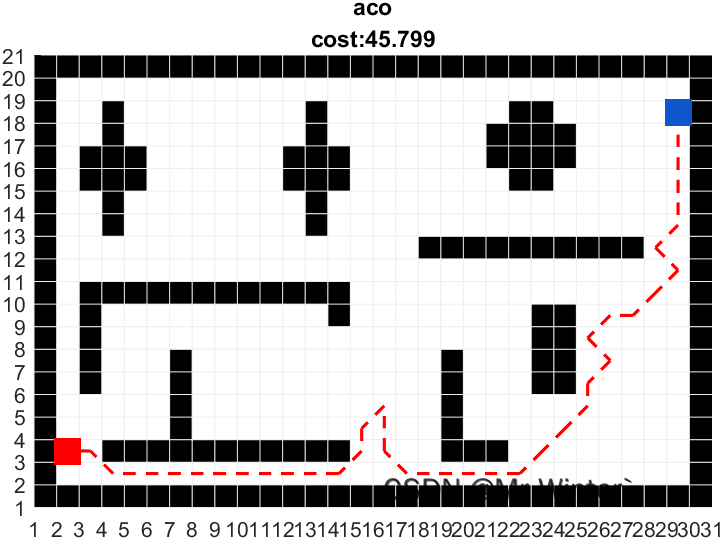
3 蚁群算法流程
蚁群算法流程如下
4 蚁群算法实现
4.1 ROS C++实现
核心代码如下所示
bool ACO::plan(const unsigned char* gloal_costmap, const Node& start, const Node& goal, std::vector<Node>& path,
std::vector<Node>& expand)
{
// pheromone initialization
...
// main loop
for (size_t i = 0; i < max_iter_; i++)
{
std::vector<Ant> ants_list = std::vector<Ant>(n_ants_);
for (size_t j = 0; j < n_ants_; j++)
{
Ant ant(start);
while ((ant.cur_node_ != goal) && ant.steps_ < max_steps)
{
ant.path_.insert(ant.cur_node_);
// candidate
float prob_sum = 0.0;
std::vector<Node> next_positions;
std::vector<double> next_probabilities;
for (const auto& m : motion)
{
Node node_n = ant.cur_node_ + m;
// next node hit the boundary or obstacle
if ((node_n.id_ < 0) || (node_n.id_ >= ns_) || (gloal_costmap[node_n.id_] >= lethal_cost_ * factor_))
continue;
// current node exists in history path
if (ant.path_.find(node_n) != ant.path_.end())
continue;
node_n.pid_ = ant.cur_node_.id_;
// goal found
if (node_n == goal)
{
ant.path_.insert(node_n);
ant.found_goal_ = true;
break;
}
next_positions.push_back(node_n);
double prob_new = std::pow(pheromone_edges[std::make_pair(ant.cur_node_.id_, node_n.id_)], alpha_)
* std::pow(1.0 / std::sqrt(std::pow((node_n.x_ - goal.x_), 2) +
std::pow((node_n.y_ - goal.y_), 2)), beta_);
next_probabilities.push_back(prob_new);
prob_sum += prob_new;
}
// Ant in a cul-de-sac or no next node (ie start surrounded by obstacles)
if (prob_sum == 0 || ant.found_goal_)
break;
// roulette selection
...
}
ants_list[j] = ant;
}
// pheromone deterioration
for (auto& pheromone_edge : pheromone_edges)
pheromone_edge.second *= (1 - rho_);
// pheromone update based on successful ants
....
}
4.2 Python实现
核心代码如下所示
def plan(self):
best_length_list, best_path = [], None
# pheromone initialization
...
# heuristically set max steps
max_steps = self.env.x_range * self.env.y_range / 2 + max(self.env.x_range, self.env.y_range)
# main loop
for _ in range(self.max_iter):
ants_list = []
for _ in range(self.n_ants):
ant = self.Ant()
ant.current_node = self.start
while ant.current_node is not self.goal and ant.steps < max_steps:
ant.path.append(ant.current_node)
# candidate
prob_sum = 0.0
next_positions, next_probabilities = [], []
for node_n in self.getNeighbor(ant.current_node):
# existed
if node_n in ant.path:
continue
node_n.parent = ant.current_node.current
# goal found
if node_n == self.goal:
ant.path.append(node_n)
ant.found_goal = True
break
next_positions.append(node_n)
prob_new = pheromone_edges[(ant.current_node, node_n)] ** self.alpha \
* (1.0 / self.h(node_n, self.goal)) ** self.beta
next_probabilities.append(prob_new)
prob_sum = prob_sum + prob_new
if prob_sum == 0 or ant.found_goal:
break
# roulette selection
...
ant.steps = ant.steps + 1
ants_list.append(ant)
# pheromone deterioration
for key, _ in pheromone_edges.items():
pheromone_edges[key] *= (1 - self.rho)
# pheromone update based on successful ants
...
if best_path:
return self.extractPath(best_path), best_length_list
return ([], []), []
4.3 Matlab实现
核心代码如下所示
% main loop
for i=1:max_iter
ants_list = struct([]);
for j=1:n_ants
% ant initialization
ants_list(j).steps = 0;
ants_list(j).found_goal = false;
ants_list(j).cur_node = start;
ants_list(j).path = [start, -1, -1]; % [x, y, px, py]
while ants_list(j).steps < max_steps && ~all(ants_list(j).cur_node == goal)
% candidate
prob_sum = 0;
next_positions = [];
next_probabilities = [];
% neighbor detection
neighbors = getNeighbor(ants_list(j).cur_node, map);
for k=1:length(neighbors)
node_n = neighbors(k, :);
% existed
if loc_list(node_n, ants_list(j).path, [1, 2])
continue
end
% goal found
if all(node_n == goal)
ants_list(j).path = [ants_list(j).path; node_n, ants_list(j).cur_node];
ants_list(j).found_goal = true;
break;
end
next_positions = [next_positions; node_n];
p_value = pheromone_edges(loc_list([ants_list(j).cur_node, node_n], pheromone_edges, [1, 4]));
prob_new = p_value ^ alpha * (1.0 / h(node_n, goal)) ^ beta;
next_probabilities = [next_probabilities, prob_new];
prob_sum = prob_sum + prob_new;
end
if prob_sum == 0 || ants_list(j).found_goal
break
end
% roulette selection
...
end
end
完整工程代码请联系下方博主名片获取
更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …