自话遗传算法(带实例)
简介
好像有那么点空闲时间,那就写点东西吧,由于近期一个项目用到了遗传算法,粒子群算法,蚁群算法等启发式智能搜索算法,今天先以本人的观点去阐述遗传算法,仅作自己对知识点的回顾,和给大家一点参考的意见,其他算法以后有时间再作描述。
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,它最初由美国Michigan大学J.Holland教授于1975年首先提出来的,并出版了颇有影响的专著《Adaptation in Natural and Artificial Systems》,GA这个名称才逐渐为人所知,J.Holland教授所提出的GA通常为简单遗传算法(SGA),这里我就直接摘抄百度百科了。
术语
种群(population)
基因(gene)
染色体(chromosome)
表现型(phenotype)
编码(codeing)
解码(decodeing)
交叉( Crossover )
突变 ( Mutation )
基本思想
正如简介所描述的那样,遗传算法是模拟达尔文的进化论思想,我想"生存竞争,适者生存"正好简要的阐述了这一算法的基本特质。用适应函数去考核每个基因的生存能力,用选择交叉变异去实现进化,搜索出种群的近似最优解,其主要步骤如下:
- 初始化种群
- 适应选择
- 交叉变异
- 迭代
算法描述
为了更好的描述,这里我以一个01背包问题为例子来简单的阐述遗传算法。
给定一个背包C=100,N=5个物品,其重量和价值分别如下,求这个背包能装的最大价值是多少
1 77 92 2 22 22 3 29 87 4 50 46 5 99 90
那么针对上面这个问题,首先我们要考虑编码,也就是把它转换成我们的基因型的形式,这里,我们用一个长度为5的二进制字符串表示相应物品的取舍。其基因型(染色体)就是10100,那么表现型就是选择了1号物品和3号物品。有编码自然就有解码,就是把基因型转换成表现型,编码个人认为是遗传算法中至关重要的一步,怎么根据问题去选择编码方式,直接影响了后面所提到的适应函数的简与复杂。
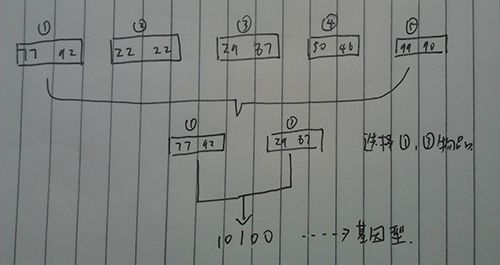
把问题映射到基因型上我们已经解决了,现在就是怎么去考核一个基因型对当前环境的适应度,换句话说就是更有可能存活遗传下去,那么这里我们必须得设计一个适应函数f,因为是求背包的最大值,又因为不能超过背包所能承受的总重量,所以用h(x)表示第二个不超过总重量的条件,f(y)表示背包的价值,所以得到适应函数f(h(x))。
然后就是怎么去选择的问题,我们用p(x)=f(y)/totall(f(y))来表示某个基因型占总体的概率,现在我们就采用轮盘赌的方法,什么是轮盘赌呢,这里简要提及一下,我们把各个概率放在一个轮盘里,然后转动这个轮盘,最后轮盘停止,指针停在哪里就代表选择哪个概率的事件。
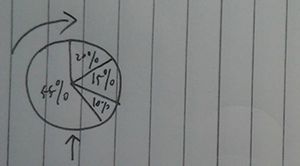
比如在01背包中,我们根据适应函数算出各个基因型的适应度,也算出了每个基因型所占的比例,然后我们根据轮盘赌的方法从中选择出n条基因型出来,然后n条基因型随机两两配对交叉产生两个子代。
交叉
那么什么是交叉呢,和生物学中染色体交叉是一样的概念,就是互换某一段基因,如下图,这里我们采用的是单点交叉。

变异
变异是指,在某一个比较小的概率下,某个基因在遗传时,某个基因座上的基因由0边成1,或者由1变成0。

新产生的基因型,如果原来的种群中没有的话,就加进这个种群,然后再按上面所述去迭代,直到找到我们比较满意的基因型为止,现在我们什么都准备好了,就让它们去交配把,去创建一个种族吧。
下面给出按照上面的例子我临时打的代码.

1 package artiano.ga; 2 3 import java.util.HashMap; 4 import java.util.Iterator; 5 import java.util.LinkedList; 6 import java.util.List; 7 import java.util.Map; 8 import java.util.Set; 9 10 class Chromosome{ 11 String key; 12 double f; 13 double p; 14 public Chromosome(String key,double f,double p){ 15 this.key=key; 16 this.f=f; 17 this.p=p; 18 } 19 public Chromosome(Chromosome o){ 20 this.key=o.key; 21 this.f=o.f; 22 this.p=o.p; 23 } 24 } 25 26 public class GAtest { 27 public Map<String,Chromosome> SAVE=new HashMap<String,Chromosome>(); 28 public List<Chromosome> list; 29 public double[][] B={ 30 {77,92}, 31 {22,22}, 32 {29,87}, 33 {50,46}, 34 {99,90} 35 }; 36 private double M=100; 37 private int N=5; 38 39 public double toPhenotype(String key){ //解码成表现型 40 41 double count=0; 42 for(int i=0;i<key.length();i++){ 43 double tmp=0; 44 if(key.charAt(i)=='1'){ 45 tmp+=B[i][1]; 46 } 47 count+=tmp; 48 } 49 return count; 50 } 51 public void init(int n){ //这里的初始化种族应该是随机的,这里为了简单起见,我随便给了一组 52 SAVE.put("10000", new Chromosome("10000",0,0)); 53 SAVE.put("01100", new Chromosome("01100",0,0)); 54 SAVE.put("00001", new Chromosome("00001",0,0)); 55 SAVE.put("01010", new Chromosome("01010",0,0)); 56 57 } 58 public String lunpandu(){ //轮盘赌 59 double nowP=Math.random(); 60 Set<String> keySet=SAVE.keySet(); 61 Iterator it=keySet.iterator(); 62 double m=0; 63 while(it.hasNext()){ 64 String key=(String)it.next(); 65 Chromosome o=SAVE.get(key); 66 m+=o.p; 67 if(nowP<=m) return key; 68 } 69 return ""; 70 } 71 public Chromosome selected(){ //选择 72 Set<String> keySet=SAVE.keySet(); 73 Iterator it=keySet.iterator(); 74 double count=0; 75 Chromosome max=new Chromosome("-1",0,0); 76 while(it.hasNext()){ 77 String key=(String)it.next(); 78 Chromosome o=SAVE.get(key); 79 count+=o.f=toPhenotype(key); 80 if(o.f>max.f) max=o; 81 } 82 it=keySet.iterator(); 83 while(it.hasNext()){ 84 String key=(String)it.next(); 85 Chromosome o=SAVE.get(key); 86 o.p=o.f/count; 87 88 System.out.println(o.key+" "+o.f+" "+o.p); 89 } 90 list=new LinkedList<Chromosome>(); 91 for(int i=0;i<2;i++){ 92 String seleKey=lunpandu(); 93 list.add(new Chromosome(SAVE.get(seleKey))); 94 System.out.println("--->"+seleKey); 95 } 96 return max; 97 } 98 99 public void crossover(){ //交叉 100 for(int i=0;i<list.size()/2;i++){ 101 Chromosome o1=list.get(i*2); 102 Chromosome o2=list.get(i*2+1); 103 int index=(int)Math.round(1+Math.random() * 2); 104 String o11=o1.key.substring(0, index); 105 String o12=o1.key.substring(index, o1.key.length()); 106 String o21=o2.key.substring(0, index); 107 String o22=o2.key.substring(index, o1.key.length()); 108 System.out.println("|||| "+o11+" | "+o12); 109 System.out.println("|||| "+o21+" | "+o22); 110 o1.key=o11+o22; 111 o2.key=o21+o12; 112 System.out.println("|||| "+o1.key); 113 System.out.println("|||| "+o2.key); 114 long bianyi=Math.round(Math.random() * 10000); 115 if(bianyi<100); 116 117 if(hefa(o1.key) && SAVE.get(o1.key)==null) SAVE.put(o1.key, o1); 118 if(hefa(o2.key) && SAVE.get(o2.key)==null) SAVE.put(o2.key, o2); 119 } 120 } 121 public boolean hefa(String key){ //是否满足h(x) 122 double m=0; 123 for(int i=0;i<N;i++){ 124 if(key.charAt(i)=='1'){ 125 m+=B[i][0]; 126 } 127 } 128 if(m<=M)return true; 129 return false; 130 } 131 public void iteration(int n){ //种群迭代 132 for(int i=0;i<n;i++){ 133 System.out.println("========="+(i+1)); 134 Chromosome max=selected(); 135 if(max.f>=133){ 136 System.out.println(" [----"+max.key+" "+max.f+" "+max.p+"-----]"); 137 break; 138 } 139 crossover(); 140 } 141 142 143 } 144 public static void main(String[] args){ 145 GAtest ts=new GAtest(); 146 ts.init(6); 147 ts.iteration(510); 148 149 } 150 151 }
打印结果:

1 =========1 2 00001 90.0 0.25069637883008355 3 10000 92.0 0.2562674094707521 4 01010 68.0 0.1894150417827298 5 01100 109.0 0.30362116991643456 6 --->01100 7 --->01100 8 |||| 01 | 100 9 |||| 01 | 100 10 |||| 01100 11 |||| 01100 12 =========2 13 00001 90.0 0.25069637883008355 14 10000 92.0 0.2562674094707521 15 01010 68.0 0.1894150417827298 16 01100 109.0 0.30362116991643456 17 --->01100 18 --->01100 19 |||| 0 | 1100 20 |||| 0 | 1100 21 |||| 01100 22 |||| 01100 23 =========3 24 00001 90.0 0.25069637883008355 25 10000 92.0 0.2562674094707521 26 01010 68.0 0.1894150417827298 27 01100 109.0 0.30362116991643456 28 --->10000 29 --->00001 30 |||| 10 | 000 31 |||| 00 | 001 32 |||| 10001 33 |||| 00000 34 =========4 35 00000 0.0 0.0 36 00001 90.0 0.25069637883008355 37 10000 92.0 0.2562674094707521 38 01010 68.0 0.1894150417827298 39 01100 109.0 0.30362116991643456 40 --->01100 41 --->00001 42 |||| 011 | 00 43 |||| 000 | 01 44 |||| 01101 45 |||| 00000 46 =========5 47 00000 0.0 0.0 48 00001 90.0 0.25069637883008355 49 10000 92.0 0.2562674094707521 50 01010 68.0 0.1894150417827298 51 01100 109.0 0.30362116991643456 52 --->00001 53 --->10000 54 |||| 00 | 001 55 |||| 10 | 000 56 |||| 00000 57 |||| 10001 58 =========6 59 00000 0.0 0.0 60 00001 90.0 0.25069637883008355 61 10000 92.0 0.2562674094707521 62 01010 68.0 0.1894150417827298 63 01100 109.0 0.30362116991643456 64 --->00001 65 --->01100 66 |||| 00 | 001 67 |||| 01 | 100 68 |||| 00100 69 |||| 01001 70 =========7 71 00000 0.0 0.0 72 00001 90.0 0.20179372197309417 73 10000 92.0 0.2062780269058296 74 01010 68.0 0.15246636771300448 75 00100 87.0 0.19506726457399104 76 01100 109.0 0.24439461883408073 77 --->01100 78 --->01010 79 |||| 0 | 1100 80 |||| 0 | 1010 81 |||| 01010 82 |||| 01100 83 =========8 84 00000 0.0 0.0 85 00001 90.0 0.20179372197309417 86 10000 92.0 0.2062780269058296 87 01010 68.0 0.15246636771300448 88 00100 87.0 0.19506726457399104 89 01100 109.0 0.24439461883408073 90 --->10000 91 --->01100 92 |||| 10 | 000 93 |||| 01 | 100 94 |||| 10100 95 |||| 01000 96 =========9 97 00000 0.0 0.0 98 00001 90.0 0.19230769230769232 99 10000 92.0 0.19658119658119658 100 01000 22.0 0.04700854700854701 101 01010 68.0 0.1452991452991453 102 00100 87.0 0.1858974358974359 103 01100 109.0 0.2329059829059829 104 --->00100 105 --->00100 106 |||| 0 | 0100 107 |||| 0 | 0100 108 |||| 00100 109 |||| 00100 110 =========10 111 00000 0.0 0.0 112 00001 90.0 0.19230769230769232 113 10000 92.0 0.19658119658119658 114 01000 22.0 0.04700854700854701 115 01010 68.0 0.1452991452991453 116 00100 87.0 0.1858974358974359 117 01100 109.0 0.2329059829059829 118 --->10000 119 --->01010 120 |||| 10 | 000 121 |||| 01 | 010 122 |||| 10010 123 |||| 01000 124 =========11 125 00000 0.0 0.0 126 00001 90.0 0.19230769230769232 127 10000 92.0 0.19658119658119658 128 01000 22.0 0.04700854700854701 129 01010 68.0 0.1452991452991453 130 00100 87.0 0.1858974358974359 131 01100 109.0 0.2329059829059829 132 --->01100 133 --->01100 134 |||| 01 | 100 135 |||| 01 | 100 136 |||| 01100 137 |||| 01100 138 =========12 139 00000 0.0 0.0 140 00001 90.0 0.19230769230769232 141 10000 92.0 0.19658119658119658 142 01000 22.0 0.04700854700854701 143 01010 68.0 0.1452991452991453 144 00100 87.0 0.1858974358974359 145 01100 109.0 0.2329059829059829 146 --->00001 147 --->10000 148 |||| 000 | 01 149 |||| 100 | 00 150 |||| 00000 151 |||| 10001 152 =========13 153 00000 0.0 0.0 154 00001 90.0 0.19230769230769232 155 10000 92.0 0.19658119658119658 156 01000 22.0 0.04700854700854701 157 01010 68.0 0.1452991452991453 158 00100 87.0 0.1858974358974359 159 01100 109.0 0.2329059829059829 160 --->00100 161 --->00001 162 |||| 001 | 00 163 |||| 000 | 01 164 |||| 00101 165 |||| 00000 166 =========14 167 00000 0.0 0.0 168 00001 90.0 0.19230769230769232 169 10000 92.0 0.19658119658119658 170 01000 22.0 0.04700854700854701 171 01010 68.0 0.1452991452991453 172 00100 87.0 0.1858974358974359 173 01100 109.0 0.2329059829059829 174 --->00100 175 --->00100 176 |||| 00 | 100 177 |||| 00 | 100 178 |||| 00100 179 |||| 00100 180 =========15 181 00000 0.0 0.0 182 00001 90.0 0.19230769230769232 183 10000 92.0 0.19658119658119658 184 01000 22.0 0.04700854700854701 185 01010 68.0 0.1452991452991453 186 00100 87.0 0.1858974358974359 187 01100 109.0 0.2329059829059829 188 --->10000 189 --->01100 190 |||| 1 | 0000 191 |||| 0 | 1100 192 |||| 11100 193 |||| 00000 194 =========16 195 00000 0.0 0.0 196 00001 90.0 0.19230769230769232 197 10000 92.0 0.19658119658119658 198 01000 22.0 0.04700854700854701 199 01010 68.0 0.1452991452991453 200 00100 87.0 0.1858974358974359 201 01100 109.0 0.2329059829059829 202 --->00001 203 --->00100 204 |||| 00 | 001 205 |||| 00 | 100 206 |||| 00100 207 |||| 00001 208 =========17 209 00000 0.0 0.0 210 00001 90.0 0.19230769230769232 211 10000 92.0 0.19658119658119658 212 01000 22.0 0.04700854700854701 213 01010 68.0 0.1452991452991453 214 00100 87.0 0.1858974358974359 215 01100 109.0 0.2329059829059829 216 --->01010 217 --->00100 218 |||| 010 | 10 219 |||| 001 | 00 220 |||| 01000 221 |||| 00110 222 =========18 223 00000 0.0 0.0 224 00001 90.0 0.1497504159733777 225 10000 92.0 0.15307820299500832 226 01000 22.0 0.036605657237936774 227 01010 68.0 0.11314475873544093 228 00110 133.0 0.22129783693843594 229 00100 87.0 0.1447587354409318 230 01100 109.0 0.18136439267886856 231 --->00001 232 --->01100 233 [----00110 133.0 0.22129783693843594-----]
最后
正如我们看见的那样,遗传算法,每次迭代都会从整个集合中去计算选择,然后通过交叉变异去产生新的种群,这样的好处显而易见,不会像梯度下降,贪心这类算法会陷入局部最优,至于其编码的选择,我想编码的好坏决定了适应函数的简单还是复杂的程度,适应函数设计的好坏决定了,整个算法是否能更快更好的收敛于近似最优。注意这里,遗传算法不能保证会得到最优解,但是在整个迭代过程,它会不断的接近于最优。
值得一提的是,遗传算法是基于图式理论的,其基因型从各个特征进行描述,这样就隐含了其搜索过程是并行处理的,对于隐含并行能力,现在已经给出了证明,每次迭代,对于n的种群,大致处理了O(n^3)个状态,这个处理能力还是相当吃惊的。
注:本博文版权属BreezeDust所有
欢迎转载,转载请注明:http://www.cnblogs.com/BreezeDust/p/3352090.html
