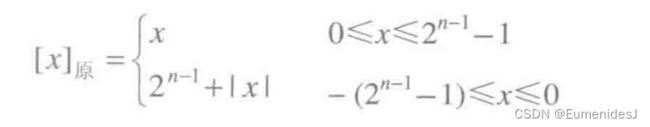计算机中的数制与编码(二进制转换)
一、进制表示
1. 十进制表示
使用(0,1,2,…,9)十位数字表示,十进制运算时逢十进一。
2. 二进制表示
使用(0,1)两个数字表示,二进制运算时逢二进一。
3. 十六进制表示
使用数字和符号(0-9, A-F)表示,十六进制运算时逢十六进一。
对于任意进制数的表示N,我们把数字k在N中的位置称为序号,用i表示(序号从右到左分别为0,1,2,…,小数部分的序号从左到右分别为-1,-2,-3,…),把能用来表示N的符号(数字)的个数称为基数,用X表示(例如二进制的基数是2,十进制的基数是10,十六进制的基数是16),把X的i次方称为第i位上的权。
二、各种数制的转换
1. 各种数制转换为十进制
各种进制转换为十进制,只要对应位上的数值乘以该位的权求和即可。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E4525YHD-1689403623568)(./进制转换.png)]
其中m为小数的位数,n为整数的位数。
例一,将二进制1101.11转换为十进制
1101.11=1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 + 1*2-1 + 1*2-2=13.75
例二,将十六进制e5ad.bf转换为十进制
e5ad.bf=14*16^3 +5*16^2+10*16^1 + 13*16^0 + 11 * 16^-1 + 15*16^-2=58797.74
2. 十进制转换成二进制
将十进制数N转换为二进制数:
- 用N除以2得到商j,余数y,取余数j0;
- 如果j不是0,则继续用j除以2,取新的余数j1;
- 重复上述步骤知道商为0,将余数从右到左排列即位对应的二进制数
...j1j0
小数部分转换为,小数部分乘以基数(2)得到值B,B取整数(0或1)先为高位,后为低位,继续取B的小数部分乘以2得值取整,直到小数部分为0。
例如:0.75转换成二进制
0.75 * 2 = 1.5,取整数部分1为二进制高位,此时小数部分不为0,继续用(1.5-1)*2=1.0,取整数部分1,此时小数部分已经为0停止计算。得到结果0.75D=0.11B
3. 十进制转换成十六进制
十进制转换为十六进制算法同二进制算法,将基数改为16即可。
4. 二进制和十六进制之间的转换
因为2的4次方等于16,所以用四位二进制表示一个十六进制数。得到二进制和十六进制之间的转换方法如下:
-
二进制转换为十六进制
以小数点为分界,整数部分从右往左,每四位一组,不足四位时高位补0,;小数部分从左往右每四位一组,不足四位时低位补0。将四位二进制数换算成10进制数值显示,10-15用A-F表示即为十六进制。
-
十六进制转换成二进制
将每一位十六进制数写成对应的四位二进制数即可。
三、二进制数的逻辑运算
- “与”,只有当两个变量的结果都为1时,结果为1
- “或”,只要有一个变量的为1,结果为1
- “非”,非0为1,非1为0
- “异或”,只要两个变量不同,结果就为1
四、带符号数的表示和运算
在计算机中为了区分正数和负数,通常用二进制数的最高位表示数的符号。对于一个字节型的二进制中最高位为符号位,剩余7位为数值为,规定用"0"代表整数,"1"代表负数,数值位表示该数的数值大小。
通常,把一个数及其符号位在机器中的一组二进制表示形式称为机器数,机器数所表示的值称为该机器数的真值。
1. 机器数的表示方法
常用的机器数的表示方法有,原码表示法,反码表示法和补码表示法。目前计算机中通常使用补码进行带符号数的运算。
1.1 原码
其中n为机器字长,x为数值。
例在8位字长的机器中
[+8]的原码=00001000 [-8]的原码=2^7 + 8=10001000
[+0]的原码=00000000 [-0]的原码=2^7 + 0=10000000
由于使用原码做数值的运算使处理器电路的设计相对复杂,所以计算机中通常使用补码做算数运算。
1.2 反码
其中n为机器字长,x为数值。
整数的反码与原码相同,负数的反码在原码的基础上,符号位不变(仍为1),数值位按位取反。
例如在8位字长的机器中
[-0]的反码=(2^8 - 1) - 0 = 11111111 [-127]的反码=(2^8 - 127)=10000000
1.3 补码
其中n为机器字长,x为数值。
正数的补码与原码、反码相同。负数的补码在原码的基础上符号位不变(为1),数值位按位取反,末位加1。
例如在8位字长机器中
[-8]的原码=10001000 [-127]的原码=11111111
[-8]的反码=11110111 [-127]的反码=10000000
[-8]的补码=2^8-8 = 11111000 [-127]的补码=2^8-127 = 10000001
可以看出来补码表示数的范围是-2^(n-1)~+2^(n-1)-1。
2. 真值和机器数的转换
2.1 原码转换为真值
将原码的数值位按权展开求和,由符号位决定数的正负即可由原码求出真值。
例如求原码x=00011111和原码y=10011101的真值
x = + (0 * 2^6 + 0 * 2^5 + 1*2^4 + 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2 ^0) = 31
x = - (0 * 2^6 + 0 * 2^5 + 1*2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2 ^0) = -29
2.2 反码转换为真值
先算出反码的原码,再由原码按照上述的方式运算即可求出反码的真值。
正数的原码等于反码本身,负数的原码在反码的基础上,符号不变(1),数值位按位取反。
例如求反码x=00001111和反码y=11100101的真值
x的原码=x的反码=00011111
x = + (0 * 2^6 + 0 * 2^5 + 0*2^4 + 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2 ^0) = 15
y的原码=10011010
y = - (0 * 2^6 + 0 * 2^5 + 1*2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2 ^0) = -26
2.3 补码转换为真值
同理,要求补码的真值,先求出补码的原码,在按上述方法计算。
正数的原码和补码相同,负数的补码在补码的基础上再次求补码。
例如以知补码x=00001111和补码y=11100101,求x和y
x的原码=x的补码=00001111
x = + (0 * 2^6 + 0 * 2^5 + 0*2^4 + 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 1 * 2 ^0) = 15
y的原码=10011011
x = + (0 * 2^6 + 0 * 2^5 + 1*2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2 ^0) = -27
五、补码的加减运算
计算机中带符号数通常用补码表示,运算结果也自然是补码,其运算特点是符号位和数值位参与运算,并且自动获得结果(包括符号位和数值位)
两数补码的和等于两数和的补码
两个补码x1,x2的减法运算为x1的补码 + (-x2)的补码=[x1 - x2]的补码
计算机中带符号数用补码表示时有如下优点
- 可以将减法运算变为加法运算,因此可以使用同一个运算器实现加法和减法运算,简化了电路。
- 无符号数和带符号数的加法运算可以使用同一个加法器实现,结果都是正确的。